
- •Тема 5. Наближення та інтерполяція функцій
- •2. Інтерполяційний многочлен Лагранжа
- •3. Похибка інтерполяції многочленом Лагранжа
- •Інтерполяція многочленом Лагранжа з рівновіддаленими вузлами
- •Інтерполяційний многочлен Ньютона
- •5. Наближення функцій, заданих таблично, методом найменших квадратів
- •Алгоритм наближення функції, заданої таблично, методом найменших квадратів
- •Тема 6 Чисельне диференціювання й інтегрування
- •1. Наближення похідних
- •2. Похибка чисельного диференціювання
- •3. Чисельне інтегрування. Поняття про квадратурні формули.
- •4. Найпростіші квадратурні формули
- •1) Формули прямокутників
- •2) Формула трапецій
- •3) Формула Сімпсона (формула парабол)
- •5. Похибки квадратурних формул
- •6. Чисельне розв’язування задачі Коші для звичайних диференціальних рівнянь
- •1) Метод Ейлера
- •2) Метод Рунге-Кутти
Розділ 3
Чисельні методи математичного аналізу
Тема 5. Наближення та інтерполяція функцій
1. Постановка задач наближення функцій
Інтерполяція функцій
Вважають,
що на множині дійсних чисел
![]() визначено деяку дійсну функцію
визначено деяку дійсну функцію
![]() ,
якщо кожному числу
,
якщо кожному числу
![]() поставлено у відповідність одне дійсне
число
поставлено у відповідність одне дійсне
число
![]() .
Разом з цим на практиці часто невідомий
прямий зв'язок між
.
Разом з цим на практиці часто невідомий
прямий зв'язок між
![]() і
і
![]() ,
тобто неможливо записати цей зв'язок у
вигляді деякої залежності
,
тобто неможливо записати цей зв'язок у
вигляді деякої залежності
![]() .
.
Нехай
при вивченні деякого явища виявилося,
що існує функціональна залежність між
змінними величинами
![]() і
і
![]() .
Найбільш поширеним і практично важливим
випадком, коли вигляд зв’язку між
.
Найбільш поширеним і практично важливим
випадком, коли вигляд зв’язку між
![]() і
і
![]() невідомий, є задання цього зв’язку у
вигляді таблиці
невідомий, є задання цього зв’язку у
вигляді таблиці
![]() .
Це означає, що дискретній множині значень
аргументу
.
Це означає, що дискретній множині значень
аргументу
![]() поставлена у відповідність множина
значень функції
поставлена у відповідність множина
значень функції
![]() ,
,
![]() .
Ці значення можуть бути знайдені в
результаті спостережень або вимірювань
в якому-небудь експерименті, або в
результаті обчислень. Але на практиці
можуть знадобиться значення величини
.
Ці значення можуть бути знайдені в
результаті спостережень або вимірювань
в якому-небудь експерименті, або в
результаті обчислень. Але на практиці
можуть знадобиться значення величини
![]() і в інших точках, відмінних від вузлів
і в інших точках, відмінних від вузлів
![]() ,
,
![]() .
.
Таким
чином приходимо до необхідності
використання наявних табличних даних
для наближеного обчислення шуканої
величини
![]() при будь-якому значення
при будь-якому значення
![]() (з деякої області). Цій меті служить
задача про наближення (апроксимацію)
функцій, яку можна сформулювати так:
дану функцію
(з деякої області). Цій меті служить
задача про наближення (апроксимацію)
функцій, яку можна сформулювати так:
дану функцію
![]() потрібно наближено замінити (апроксимувати)
деякою простою функцією
потрібно наближено замінити (апроксимувати)
деякою простою функцією
![]() так, щоб відхилення в деякому розумінні
так, щоб відхилення в деякому розумінні
![]() від
від
![]() в заданій області було б найменшим.
Функція
в заданій області було б найменшим.
Функція
![]() при цьому називається апроксимуючою.
при цьому називається апроксимуючою.
Часто
апроксимуючу функцію
![]() беруть у вигляді многочлена:
беруть у вигляді многочлена:
![]() .
.
Щоб задати многочлен, треба задати тільки скінченну кількість його коефіцієнтів. Значення многочлена просто обчислюються, його легко продиференціювати, проінтегрувати і т.і. Тому алгебраїчні многочлени знайшли широке застосування для наближення (апроксимації) функцій.
Апроксимація,
при якій наближення будується на заданій
дискретній множині точок
![]() ,
називається точковою.
,
називається точковою.
Одним з основних типів точкової апроксимації є інтерполяція.
Постановка
задачі інтерполяції.
Нехай відомі значення деякої функції
![]() у
у
![]() різних точках
різних точках
![]() з відрізку
з відрізку
![]() ,
які позначимо
,
які позначимо
![]() ,
,
![]() .
Для функції
.
Для функції
![]() треба побудувати функцію
треба побудувати функцію
![]() (наприклад, у вигляді многочлена), яка
набуває в заданих точках
(наприклад, у вигляді многочлена), яка
набуває в заданих точках
![]() ті ж самі значення
ті ж самі значення
![]() ,
що й функція
,
що й функція
![]() :
:
![]() ,
,
![]() . (1)
. (1)
Точки
![]() ,
,
![]() називаються вузлами
інтерполяції. Формула
називаються вузлами
інтерполяції. Формула
![]() ,
знайдена для обчислення значень функції
,
знайдена для обчислення значень функції
![]() називається інтерполяційною.
називається інтерполяційною.
З
геометричної точки зору задача
інтерполяції полягає в знаходженні
лінії
![]() ,
що проходить через точки площини з
координатами
,
що проходить через точки площини з
координатами
![]() ,
,
![]() ,
…,
,
…,![]() :
:
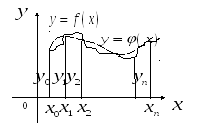
На
практиці систему
![]() часто беруть у вигляді цілих невід'ємних
степенів змінної
часто беруть у вигляді цілих невід'ємних
степенів змінної
![]() ,
тобто
,
тобто
![]() .
Тоді
.
Тоді
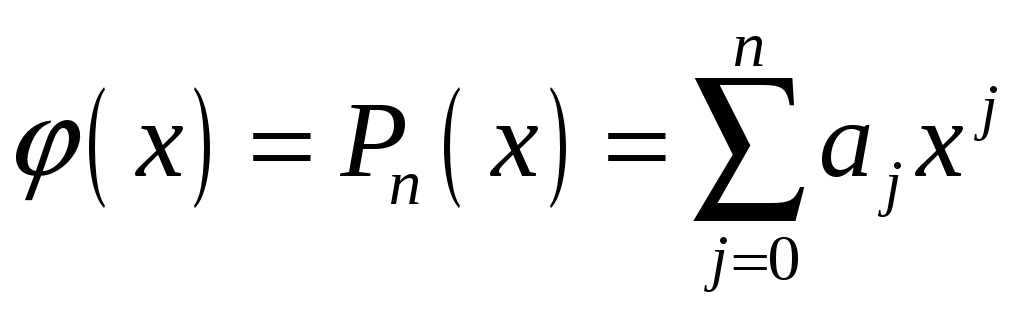 і
і
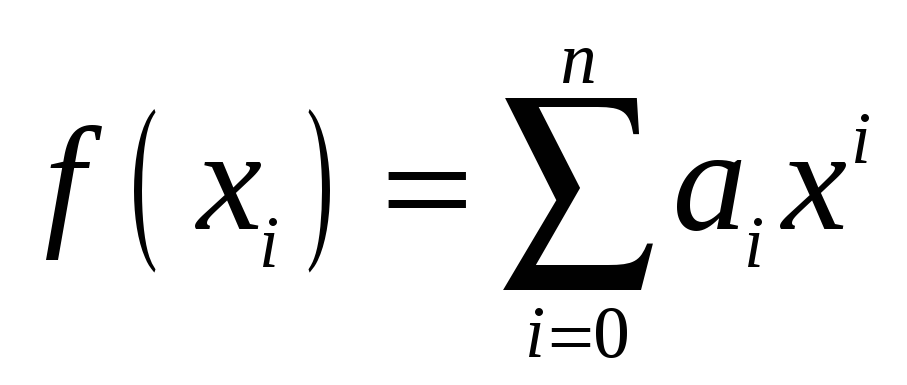 (2)
(2)
тобто
інтерполяція здійснюється многочленом
![]() ,
який називається інтерполяційним.
Інтерполяція в цьому випадку називається
поліноміальною.
,
який називається інтерполяційним.
Інтерполяція в цьому випадку називається
поліноміальною.
Система
рівнянь (2) є системою лінійних алгебраїчних
рівнянь відносно невідомих коефіцієнтів
![]() і має вигляд:
і має вигляд:
 (3)
(3)
Теорема
(про єдиність розв'язку задачі
інтерполяції).
Якщо при будь-якому розміщенні вузлів
інтерполяції, серед яких немає таких
що збігаються, визначник системи
(3)
не дорівнює нулю, то існує єдиний
інтерполяційний многочлен
![]() -го
ступеню.
-го
ступеню.
Таким чином, інтерполяційний многочлен можна одержати шляхом розв’язання системи лінійних алгебраїчних рівнянь (3). Такий метод побудови інтерполяційного многочлену називається методом невизначених коефіцієнтів. Відзначимо, що цей метод потребує значного об’єму обчислень. Існують більш прості алгоритми побудови інтерполяційного многочленну, які розглянемо нижче.
