
- •Часть 2
- •Часть 2
- •Содержание
- •Введение
- •1. Требования к выполнению контрольной работы
- •2. Основные формулы, термины и определения
- •Раздел "Интегральное исчисление функции одной переменной"
- •3. Примерный вариант контрольной работы №2 Задание № 1 по теме "Дифференциальное исчисление функции одной переменной"
- •Задание № 2 по теме "Интегральное исчисление функции одной переменной"
- •4. Решение примерного варианта контрольной работы Задание № 1 по теме "Дифференциальное исчисление функции одной переменной"
- •Задание № 2 по теме "Интегральное исчисление функции одной переменной"
- •5. Варианты контрольных работ для слушателей зачного отделения
- •Контрольная работа № 2
- •Вариант № 1
- •Задание № 1
- •Задание № 2
- •Вариант № 4 Задание № 1
- •Задание № 2
- •Вариант № 5 Задание № 1
- •Задание № 2
- •Вариант № 6 Задание № 1
- •Задание № 2
- •Вариант № 7 Задание № 1
- •Задание № 2
- •Вариант № 8 Задание № 1
- •Задание № 2
- •Вариант № 9 Задание № 1
- •Задание № 2
- •Вариант № 10 Задание № 1
- •Задание № 2
- •Рекомендуемая литература
- •Образец оформления титульного листа контрольной работы
- •Часть 2
Задание № 2 по теме "Интегральное исчисление функции одной переменной"
Задача 1. Вычислить неопределенный интеграл
![]() .
.
![]()
Решение
Для вычисления интеграла, воспользуемся свойствами неопределенного интеграла ((20) – (24)) и таблицей интегралов (см. таб.2), предварительно представив подынтегральную функцию в виде суммы трех функций:
![]()
![]() .
.
Прежде, чем записать ответ, целесообразно сделать проверку. Производная полученной в результате интегрирования функции должна быть равна подынтегральной функции, т.е. должно выполняться соотношение (17).
Проверка:
![]() .
.
Ответ:
![]() .
.
Задача 2.
Вычислить неопределенный интеграл
![]() .
.
Р
![]()
1. Первый способ.
Воспользуемся свойством инвариантности
(24). Для этого предварительно вычислим
дифференциал
![]() .
Тогда
.
Тогда
![]() и окончательно получим
и окончательно получим
![]() 2.
Второй способ. Используем метод
замены переменной (метод подстановки).
Введем новую переменную
2.
Второй способ. Используем метод
замены переменной (метод подстановки).
Введем новую переменную
![]() .
.
Вычислим дифференциал
![]() ,
,
тогда:
![]() ,
,
![]() .
.
Вернемся к старой
переменной
![]() (сделаем обратную подстановку)
(сделаем обратную подстановку)
![]() .
.
Проверка:
![]() .
.
Ответ:
![]() .
.
Задача 3.
Вычислить неопределенный интеграл
![]() .
.
![]()
Решение
Заметим, что в исходном интеграле
![]() ,
,
тогда, внося функцию под знак дифференциала, получим
![]() .
.
Проверка:
![]() .
.
Ответ:
![]() .
.
Задача 4.
Вычислить определенный интеграл
![]() .
.
Решение
Вычислим определенный интеграл по формуле Ньютона-Лейбница (27):
![]() .
.
Подставляя пределы интегрирования, получим
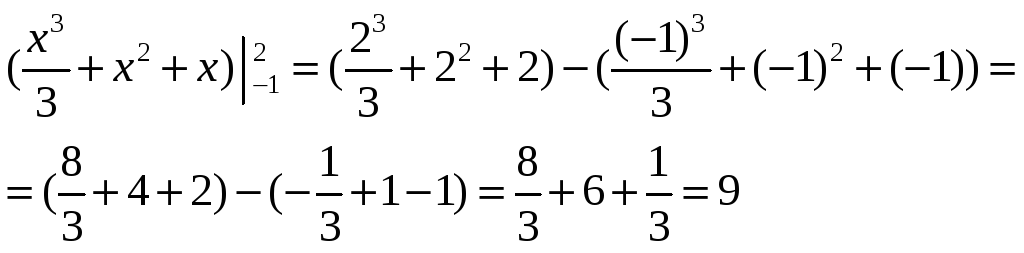 .
.
Ответ: 9.
Задача 5.
Вычислить определенный интеграл
![]() .
.
Решение.
1. Найдем неопределенный
интеграл
![]() ,
используя метод интегрирования по
частям.
,
используя метод интегрирования по
частям.
В формуле интегрирования по частям (25)
![]()
положим
![]() ;
; ![]() .
.
тогда
![]() ;
; ![]() ,
,
![]() .
.
Применим интегрирование по частям к последнему интегралу:
![]() .
.
Таким образом,
![]() ,
,
откуда окончательно получим
![]() .
.
2. Вычислим исходный определенный интеграл, подставляя пределы интегрирования в соответствии с формулой Ньютона-Лейбница (27):

Ответ:
![]() .
.
Задача 6.
Вычислить определенный интеграл
![]()
Решение.
Используем метод замены переменной (29). Введем новую переменную:
![]() ,
,
вычислим
![]() .
.
Определим новые
пределы интегрирования из равенства
![]() :
:
при x =
1 получим
![]() ,
,
при x =
2 получим
![]() .
.
Меняя переменную и вычисляя интеграл по формуле Ньютона-Лейбница (27), получим:
![]() .
.
Ответ:
![]() .
.
Задача 7. Решить дифференциальное уравнение
![]() .
.
Решение.
Исходное уравнение является дифференциальным уравнением с разделяющимися переменными. Разделим переменные, выполняя следующую последовательность действий:
1. Представим в
исходном уравнении производную![]() в
виде
в
виде
![]() :
:
![]() .
.
2. Умножим обе части
уравнения на
![]() :
:
![]()
3. Разделим
переменные, поделив обе части уравнения
на
![]() :
:
![]() .
.
4. Проинтегрируем обе части уранения:
![]() ,
,
![]() 3
3
Преобразуем полученное ввыражение
![]() ,
,
![]() ,
,
откуда получим общее решение уравнения:
![]()
Ответ:
![]() .
.
Задача 8. Решить задачу Коши:
![]() ;НУ:
у (0) = –3.
;НУ:
у (0) = –3.
Решение
1. Найдем общее решение дифференциального уравнения. Так как уравнение является простейшим, то его решение находится интегрированием функции, стоящей в правой части уравнения:
![]() .
.
2. Найдем значение произвольной постоянной С, соответствующее частному решению дифференциального уравнения, подставляя в общее решение начальное условие у = –3, х = 0:
![]() .
.
3. Запишем частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Для этого подставим найденное значение произвольной постоянной С= –3 в общее решение уравнения:
![]() .
.
Сделаем проверку:
![]() .
.
Ответ:
![]() .
.
