Ответы на экзамен Котюргина / saaty

A(t )

опускающемся до минимума и возрастающем, колебательном и, наконец, допускающем катастрофическое изменение.

Матрица 2×2

Для этого случая λmax (t )= 2 и наша зависимая от времени задача о собственном значении представляется в виде

	1	a(t ) ω		(t )	= 2	ω	(t )
		1	1			1	,
1/ a(t )			ω2 (t )			ω2 (t )

откуда имеем

ω1 (t )+ a(t )ω2 (t )= 2ω1 (t ), ω1 (t )/ a(t )+ω2 (t )= 2ω2 (t ).

Из первого уравнения получаем

ω1 (t )= a(t )ω2 (t ),

что также может быть получено из второго уравнения. Эти два уравнения не могут быть независимыми, в противном случае детерминат не был бы равен нулю

и мы не имели бы ненулевого решения. Поэтому можно зафиксировать ω2 (t ) произвольным образом, например положить ω2 (t )=1, отсюда получим ω1 (t )= a(t ). Нор-

мализованный правый собственный вектор имеет вид {a(t )/ a(t )+1 , 1/ a(t )+1 }.

Нормализованный левый собственный вектор будет обратным элементом, т. е.

{1/ a(t ) a(t )+1 , 1/ a(t )+1 }

Матрица 3×3

Моррис [109], решая кубическое уравнение, достаточно просто показал, что λmax для случая 3×3 при aij =1/ aji представляется в виде

λmax = (a13 / a12a23 )1/ 3 +(a12a23 / a13 )1/ 3 +1

Заметим, что λmax всегда ≥ 3 (мы доказали, что в общем случае λmax ≥ n ). Система уравнений, соответствующая этому случаю, представляется следующим

образом:

ω1 (t )+ a12ω2 (t )+ a13ω3 (t )= λmax (t )ω1 (t ), ω1 (t )/ a12 +ω2 (t )+ a23ω3 (t )= λmax (t )ω2 (t ), ω1 (t )/ a13 +ω2 (t )/ a23 +ω3 (t )= λmax (t )ω3 (t ).

Положим ω1 =1. Первое уравнение будет

a12ω2 (t )+ a13ω3 (t )= −(1−λ),

а второе –

(1−λ)ω2 + a23ω3 = −1/ a12 .

Решим их теперь относительно ω2 и ω3 . Получим

91

ω2 = (λ −1)a23 +(a13 / a12 )

,

∆

ω3 =

−1+

(1−λ)2

,

∆

где ∆ = a12a23 + a13 (λ −1).

Чтобы нормализовать компоненты, образуем

ω +ω

2

+ω

3

=

a12a23 + a13 (λ −1)a23 +(a13 / a12 )−1+(1−λ)2

≡

D

.

1

∆

∆

Следовательно,

ω1 = ∆/ D ,

ω2 = (λ −1)a23 +(a13 / a12 )

,

D

ω3 =

−1+

(1−λ)2

.

D

Для левого собственного вектора, который является поэлементно обратным, имеем:

	υ =		−1+(1−λ)2
	1			E
υ2 =		a12 (λ −1)+(a13 / a23 )						,
				E
		υ3 = ∆/ E ,
где
E = −1+(1−λ)2 + a		(λ −1)+(a / a					)+ a a + a				(λ −1).
12				13	23		12		23	13
		Матрица 4×4
Рассмотрим обратносимметричную			матрицу		4 ×4 с				элементами, являющимися
функциями времени			a	b			c
	1
A =	1/ a		1	d			e
			1/ d	1
	1/ b						f .
			1/ e	1/ f
	1/ c						1

Отметим, что все коэффициенты могут быть функциями параметра t . Характеристическое уравнение этой матрицы

λ4 − 4λ3 −(B −8)λ +(B +C −5)= 0 ,

где

df

e

ae

c

ad

b

bf

c

B =

+

+

+

+

+

+

+

,

e

ae

df

c

b

ad

c

bf

adf

c

ae

bf

cd

cd

be

C = 3 −

c

+

−

+

−

−

+

.

adf

bf

ae

ae

be

cd

Рассмотрим редукцию уравнения четвертой степени следующим образом:

92

(λ2 − 2λ)= (B −8)λ −(B +C −5)+ 4λ2 .

Добавляя

(λ2 −2λ)r + 14 r2

( r – параметр) к обеим частям уравнения, получаем

		2		1	2		2			1		2
	λ		−2λ +		r	= (r + 4)λ		+(B −8	− 2r)λ +		r		−(B +C −5).
				2						4

Правая часть является полным квадратом линейной функции по λ в том и только в том случае, если ее детерминант равен нулю, т. е.

∆= (B −8)− 2r 2 − 4 14 r2 −(B +C −5) (r + 4)=

=−r3 + 4(c +3)r +(−16 + B2 +16C)= 0 ,

иназывается кубической резольвентой уравнения четвёртой степени. Если r – корень этого уравнения, то ∆ = 0 . Имеем

2

1

2

B − 2(r + 4)

2

B

2

λ

− 2λ +

r

= (r + 4) λ +

= (r + 4)

λ −1

+

,

2

2(r + 4)

2(r + 4)

откуда при использовании наибольшего значения r получим

λ

=

2 + r + 4

+

8 − r

+

B

.

max

2

4

2 r + 4

Теперь посмотрим, как решается кубическое уравнение. Кубическую резольвенту можно представить в виде

r3 + pr + q = 0 ,

где p = −4(C +3), q =16 − B2 −16C .

Используя преобразование						p
		r = z −					,
запишем резольвенту в виде						3z
z	3	−	p3		+ q = 0
			27z3

или

z6 + qz3 − p3 = 0 ,

27

а это – квадратное уравнение по z3 . Таким образом, решения будут

z3 = − q	± R ,
2

где R = (p / 3)3 +(q / 2)2 . Пусть

T = 3	− q +	R , T = 3	− q −	R .
1	2	2	2

Кубические корни из единицы будут

93

1 , ω1 = −	1	+	1	3i , ω2 = −	1	−	1	3i .
	2		2		2		2

Получаем следующие шесть решений

T1 , ω1T1 , ω2T1 , T2 , ω1T2 , ω2T2

уравнения

z6 + qz3 − p3 = 0 .

27

Известно, что корни приведённого кубического уравнения r3 + pr + q = 0 представляются в виде

																r1 = T1 +T2 ,
														r =ω1T +ω2T																	,
														2				1										2
														r =ω2T +ω1T .
														3				1										2
Поэтому
					B		2												4											3							B		2				2	1/ 3
	r = −8 +								+	8C			+			−					(C +3)										+				8 −						−8C			+
	1			2																															2
																3
				B		2										−		4		(C +3)								3								B		2				2		1/ 3
		+ −8 +						+		8C			−																		+		8 −								−8C				,
				2													3
																																			2
											1			1											1							1
				r2			=			−		+				3i		T1 +						−						−					3i T2						=
											2			2											2							2
									r = − 1 (T +T )+															3			(T −T )i ,
								2					2			1		2						2							1				2
				r3						−	1	−		1		3i								−	1					+		1									=
						=					2			2				T1 +							2							2			3i T2
									r = − 1 (T +T )−															3		(T −T )i .
								2					2			1		2						2							1				2
Если T = T		, R = 0			и			корни						r		= r = (−q / 2)1/ 3 .																			действительны;											r = 2	(−q / 2)1/ 3 .
1	2													2			3																													1
Кроме того, поскольку корни комплексно-сопряжённые, r1																																									всегда является действи-
тельным корнем кубической резольвенты.																						Это следует из того факта, что p ≥ 0 .

Чтобы понять это, отметим, что C имеет три члена вида x +1/ x . Минимальное зна-

чение такого члена равно 2, т. е. C ≤ −3 и	p = −4(C +3)≥ 0 . Поэтому r = r1	всегда
действителен. К тому же r ≥ 0 , так как q ≤ 0 . Это следует из
B2 +16C ≥16 ,
B2 ≥16(1−C).
Минимум 16(1−C) есть 64.
Аналогично минимальное значение B2	есть 64. Поэтому q ≤ 0 . Итак,	первый
член из выражения для r1 положителен и,	кроме того, всегда превосходит второй.

94

Поэтому r = r1 ≥ 0 является корнем, который используется выше в выражении для

λmax .

Решение системы Aω = λmaxω , которое в развернутой форме имеет вид

(1−λ)ω1 + aω2 + bω3 + cω4 = 0 , a1 ω1 +(1−λ)ω2 + dω3 + eω4 = 0 , b1 ω1 + d1 ω2 +(1−λ)ω3 + f ω4 = 0 ,

1c ω1 + 1e ω2 + 1f ω3 +(1−λ)ω4 = 0 ,

после нормализации будет:

ω =ω0 / Q , ω

2

=ω

0 / Q ,

ω

3

=ω0 / Q ,

ω

4

=ω0

/ Q ,

1

1

2

3

4

где

3

2

1

1

e

Q = (λ −1)

+(c + f + e)(λ −1)

+

(ae

−3)+(b + d ) f +

+

c

+

(λ −1)+

a

b

d

be

bf

cd + ae c −b

(adf − a −e − f )

+

+

+

b

ad

,

d

ba

ω0

= c(λ −1)2

+(ae + bf )(λ −1)

+

adf +

be

− c

,

1

d

0

2

c

bf

cd

ω2

= e(λ −1)

+ df

+

(λ −1)

+

+

−e ,

a

a

b

0

= f (λ −1)

2

e

c

(λ −1)+

c

ae

− f

ω3

+

+

+

,

b

b

d

ad

0

= (λ

1)

2

−3(λ

−1)−

ad

b

ω4

−

+

.

b

ad

Замечание. Из полученного решения видно, что если любой коэффициент увеличивается (уменьшается) в данной строке матрицы парных сравнений, то величина компоненты собственного вектора, соответствующей этой строке, увеличивается (уменьшается) относительно остальных компонент. Это свойство присуще и общему случаю для обратносимметричной матрицы.

В завершении этого раздела рассмотрим простой случай семьи, состоящей из отца (О), матери (М) и ребенка (Р). Очевидно, что время, которое ребенок проводит дома, завись г от его возраста. Ребенок будет находиться дома то же время, что и мать, а затем, взрослея, он будет проводить дома все меньше времени по сравнению с тем временем, которое проводит дома мать. Предполагается, что мать не ходит на работу.

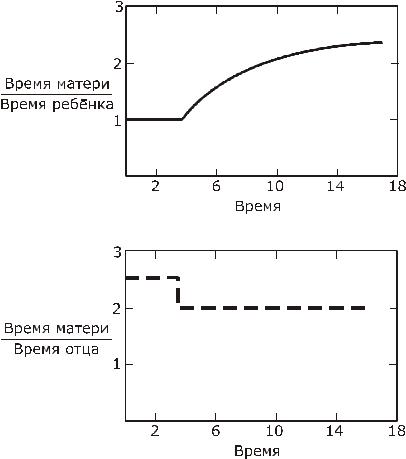
Если сравнить время, проводимое дома матерью и ребенком, и составить диаграмму этого отношения как функцию времени, то получим кривую, показанную на рис. 5.1.

Кривая начинается с одинакового времени, которое проводит дома мать и ребенок, затем отношение времени матери к времени ребенка растет, пока кривая не станет горизонтальной. Это произойдет ко времени, когда ребенок достигло 15–16 лет.

95

Сравнение времени, проводимого дома отцом и ребенком, дает отношение, которое является зеркальным отражением верхней кривой. Это отношение показано на рис. 5.2. Относительная величина времени, проводимая дома отцом и матерью, не будет меняться слишком сильно и можно предположить, что она более или менее постоянна.

Рис. 5.1

Рис. 5.2

Если требуется провести парные сравнения различных промежутков времени, проводимых дома различными членами семьи, то нужно получить последовательность матриц сравнения, каждая из которых соответствовала бы определенному периоду времени.

Рассмотрим период времени, соответствующий возрасту ребёнка до четырех лет. Если исключить, скажем, восемь часов ночью, то можно ожидать, что мать и ребёнок проводят примерно в 2–3 раза больше времени дома, чем отец. Конечно, мать и ребёнок проводят дома одно и то же время.

Это дает следующую матрицу:

O	M	P
O 1	1/ 2,5	1/ 2,5
	1	1
M 2,5
	1	1
P 2,5

λmax = 3,0 ; ИС = 0,0; ОС = 0,0

Отсюда получаем следующий собственный вектор для их относительного времени пребывания дома

О: 0,167; М : 0,417; Р: 0,417 ,

который разумно отражает соответствующие пропорции времени.

96

Примерно в четыре года ребенок начинает ходить в детский сад, так что происходит разное изменение в относительных пропорциях времени, проводимом дома матерью с ребенком и отцом с ребенком.

Изменяющиеся пропорции в одной матрице можно записать, используя зависящее от времени выражение для этих пропорций

		O	M	P
O		1	1/ 2	1/ (3 −1nt / 2)
		2	1
M				0,4 +1nt / 2
P		−1nt / 2	1/ (0,4 +1nt / 2)	1
	3

где t – возрастной период от 4 до 16 лет.

Эта матрица, наряду с предыдущей, приводит к кривым на рис. 5.3–5.5, которые изображают соответствующие парные сравнения при изменении возраста от нуля до

16 лет.

Рис. 5.3. Мать и ребёнок: возраст от 0 до 16 лет

Рис. 5.4. Отец и мать: возраст от 0 до 16 лет

97

Рис. 5.5. Отец и ребёнок: возраст от 0 до 16 лет

Решение задачи о максимальном собственном значении, соответствующем этим кривым парных сравнений для (4 ≤ t ≤16), будет

		2		1/ 3		(3 −1nt / 2)(0,4	+1nt / 2) 1/ 3
λ =					+			.
	(3	−1nt / 2)(0,4				2
			+1nt / 2)

Соответствующий собственный вектор получается в виде ∆/ D ,

2

(λ −1)(0,4

+1nt / 2)+

/ D ,

3 −1nt / 2

−1+(1−λ)2

/ D ,

где

λ −1

∆ = 0,5(0,4 +1nt / 2)+

,

3

−1nt / 2

D = (λ −0,5)(0,4 +1nt / 2)+

λ +1

−1

+(1−λ)2 .

3 −1nt / 2

По окончании школы ребенок проводит дома меньше времени, чем отец. Пропорции еще раз становятся довольно постоянными и отражаются в следующей согласованной матрице парных сравнений:

O	M	P
O 1	0,5	1,25
	1
M 2		2,5
	0,4
P 0,8		1

λmax = 3,0 ; ИС = 0,0; ОС = 0,0

Собственный вектор будет

О: 0,263; М : 0,526; Р: 0,211 .

98

Рис. 5.6. Сравнительное время, проводимое дома

Построение результирующих диаграмм для 0 ≤ t ≤ 4 , 4 ≤ t ≤16 и 16 ≤ t реалистически воспроизводит сравнительное время, по отношению ко всем остальным членам семьи, которое каждый член семьи проводит дома (рис. 5.6).

5.5. ИЗМЕРЕНИЕ ВЗАИМОСВЯЗЕЙ МЕЖДУ ПРОИЗВОДСТВЕННЫМИ СПОСОБАМИ:

ВХОД–ВЫХОД; ПРИЛОЖЕНИЕ К СУДАНУ

При изучении взаимосвязей особое внимание уделим отношениям типа «вход– выход». Матрицы модели «вход–выход» в экономике получаются в общем виде следующим образом.

Пусть даны N секторов экономики A1, A2 ,…, AN и матрица S ; элемент матрицы sij обозначает выход сектора i , который становится входом сектора j (это промежуточная продукция сектора i . необходимая сектору j ). Выход из сектора i к потребителю (конечная продукция) обозначим через Yi . Имеем

N		общая промежуточная продукция сектора i (внутренние по-
∑sij = Si	–
j=1		требности других секторов)
Si +Yi = Oi	–	общая (валовая) продукция сектора i

Коэффициенты прямых затрат* получаются следующим образом:

sij	−ωij – (вклад сектора i в производство единицы общей продукции j
Si +Yi

* Называются также технологическими коэффициентами. – Прим. перев.

99

sij

=

sij

S

i

=

sij Si

S

i

+Y

S

ii

S

i

+Y

S O

i

i

i i

Для получения матрицы прямых затрат посредством МАИ нужно оценить sij / Si и

Si / Oi . Посмотрим, что они представляют из себя. Si / (Si +Yi ) – доля общей продук-

ции сектора i , распределяемой для собственного потребления. Общая промежуточная продукция оценивается для i =1, 2,…, N посредством МАИ после ответа на сле-

дующий вопрос: насколько один сектор важнее по сравнению с другим при распределении выходной продукции на собственные нужды? Если на этот вопрос нельзя ответить прямо, то внутренние потребности могут быть иерархически разделены на производство, спрос, людские ресурсы, капитал и стоимость, и секторы получают приоритеты отдельно относительно каждого критерия. После определения приоритетов этих критериев по отношению к их влиянию на производство используется композиция для получения общей меры важности для секторов. Обозначим оценки

Si / Oi через xi .

Вновь sij / Si представляет собой долю общей промежуточной продукции сектора i . распределенную в секторе j . Имеем

N

∑sij / Si =1 j=1

Построим матрицу парных сравнений между секторами по отношению к сектору i . Ответим на следующий вопрос: насколько сильна зависимость одного сектора по сравнению с другим для получения выходной продукции из сектора i ? В результате имеем матрицу парных сравнений, из которой получаем собственный векторстолбец весов. Когда это проделано для каждого сектора, получаем матрицу W , столбцами которой будут собственные векторы.

Наконец, для получения оценок коэффициентов прямых затрат, т. е. матрицы «вход–выход», поэлементно умножим каждый столбец матрицы W на вектор-

столбец x = (x1, x2 ,…, xN ).

Самым важным фактором, который следует принять во внимание при оценке матрицы прямых затрат, используя иерархический подход, является доля промежуточной продукции в каждом секторе относительно всей продукции. Оценка этой доли была проведена в предлагаемом примере после тщательного изучения существующей литературы по экономике Судана [139]. Рассматривались следующие шесть секторов:

1.Сельское хозяйство (СХ).

2.Коммунальное хозяйство (КХ).

3.Промышленность и добыча полезных ископаемых (ПД).

4.Транспорт и доставка товаров (ТД).

5.Строительство (СТ).

6.Сервис (СЕ).

Судан рассматривается в основном как аграрная страна. К тому времени, когда разрабатывались эконометрические модели (1972 г.) и проводился анализ «вход– выход», использовались данные за 1961 г. Основной проблемой в Судане было отсутствие достаточно эффективной транспортной системы. Для получения одинакового порядка величин оценок секторов, сравниваемых с сельским хозяйством и транспортом (другим крупным видом деятельности), остальные секторы были сгруппированы в одно целое – агрегат. Таким образом, имеем:

100