Ответы на экзамен Котюргина / saaty

A , кото-

и предел в правой стороне должен существовать, что возможно только при h = λ или h < λ , причем в последнем случае предел равен нулю.

Собственное значение λ есть главное собственное значение матрицы рое обозначается λmax , а υ и ω – главные собственные векторы матрицы A .

Следствие. Главный собственный вектор-строка (столбец) — υ(ω) ортогонален

ко всем не главным собственным векторам-столбцам (строкам) матрицы A . Доказательство. Рассмотрим равенство ωυu = 0 из доказательства предыдущей

теоремы. Так как ω > 0 , имеем υu = 0 , и, следовательно, υ ортогонален векторустолбцу u . Аналогичный аргумент можно использовать, чтобы показать ортогональность ω ко всем не главным собственным векторам-строкам матрицы A .

Следствие. υω =1.

Доказательство. В условиях теоремы пусть u =ω , тогда h = λ и ωυω =ω . Так как υω – число, получаем υω =1.

Замечание. υω есть след матрицы ωυ , и, следовательно, этот след всегда равен единице.

n

Замечание. Система ∑aij xj

= bi

, i =1, …, n .

j=1

где aij ≥ 0 , dij > 0 , имеет неотрицательное решение xj

≥ 0 ,

j =1, …, n , если

a11

a12

a11

a12

a13

a11 > 0,

> 0,

a21

a22

a23

> 0, …,

A

> 0 .

a

a

21

22

a31

a32

a33

Теорема 7.11 [182]. Если

A – неотрицательная неприводимая матрица, то зна-

чение λmax

возрастает с увеличением любого элемента aij .

Доказательство. Пусть

A – неотрицательная матрица, определим B (ρ)= ρI − A ,

где ρ – действительный параметр [110]. Пусть M – множество всех ρ , для кото-

рых существует и не отрицательна обратная матрица (ρI − A)−1 . Множество M не-

пусто для

x > 0 и остается таким для сравнительно большого ρ , ρx > Ax , т. е.

ρx − Ax > 0 ,

и это условие обеспечивает существование неотрицательного решения

и эквивалентно вышеописанному условию на главные миноры. Так как M зависит

от A , обозначим его M (A).

Пусть

′

≥

′′

′

′′

В самом

деле, заметим, что если

A

A ≥ 0 . Тогда M (A ) M (A ).

ρ M (A′),

то

(ρI − A′)x > 0

для некоторого

x > 0

и

так

как ρI − A′′ ≥ ρI − A′,

(ρI − A′′)x > 0

для того же самого

x , и, следовательно,

ρ M (A′′). Теперь макси-

мальное собственное

значение λmax

матрицы

A > 0

есть

inf ρ , для которого

ρ M (A)

(ρI − A)−1

существует,

т. е. это первое значение, для которого

ρI − A

= 0 , ибо все

другие собственные значения не превосходят λmax . Поэтому

λ

(A′)= inf ρ ≥ inf ρ

= λ

(A′′).

max

′

′′

max

ρ M (A )

ρ M (A )

161

Следовательно, λmax – монотонная функция A .

Ниже показан важный результат, который заключается в том, что собственный вектор, соответствующий λmax , представляет собой нормализованные суммы элемен-

тов строк предельной матрицы в точности k -й степени

Ak -матрицы A (а не суммы

всех степеней A ).

Теорема 7.12.

lim

Ak e

= cω

,

k

→∞ eT Ak e

1

где A > 0 , ω1 – главный собственный вектор, соответствующий максимальному соб-

ственному значению λ1 , λi

≠ λj

для всех i

и

j ,

ωi

–

правый собственный вектор,

соответствующий λi , а c – постоянная.

Доказательство. e = a1ω1 +…+ anωn , где ai ,

i =1, …, n – постоянные.

Ak e = a1λ1kω1 +…+ anλnkωn

= λ1k a1ω1 + a2

(λ2

λ1 )k ω2 +…+ an (λn

λ1 )k ωn ,

eT Ak e = λk

b

+b

(λ λ )k +…+b (λ λ )k ;

b = a eTω .

1

1

2

2

1

n

n

1

i i

i

Так как ω1 > 0 , b ≠ 0 , что и требовалось доказать.

Теперь обобщим эту теорему.

Определение 7.2. Неотрицательная неприводимая матрица A примитивна то-

гда и только тогда, когда существует целое m ≥1. такое, что Am > 0 . В противном случае матрицу называют импримитивной. Граф примитивной матрицы имеет длину пути между любыми двумя вершинами ≥ m .

Из работ [50, 114, 182] известно, что неотрицательная неприводимая матрица A

примитивна тогда и только тогда, когда A имеет единственный характеристический корень с максимальным модулем, и этот корень имеет кратность, равную единице.

Теорема 7.13. Для примитивной матрицы A
lim		Ak e		= cω ,		Ak		≡ eT Ae	,
		Ak
k →∞

где c – постоянная, а ω – собственный вектор, соответствующий λmax ≡ λ1 .

Доказательство. Допустим A > 0 . Рассмотрим жорданову каноническую форму B матрицы A . Тогда для некоторой невырожденной матрицы N

λ		0
	1
NAN −1 =	B2			= B
		.
. .
	0	Br

где Bi , i = 2, …, r есть mi ×mi жорданова блочная форма, которая имеет вид

162

	λi
	1
		λi	0
		1
		λi
Bi =		1
	. . .		. . .	.
			λi
	0
			1
				λ
				i

где λ2 , …, λr – различные собственные значения с кратностями m2 , …, mr соот-

r
ветственно, а 1+∑mi = n – размерность матрицы A . Выбираем соответствующие
i=2
базисные векторы для каждого подпространства жордановой формы
V1
V21,	V22 , …,	V2m2
V31,	V32 , …,	V3m3
Vr1,	Vr 2 , …,	Vrmr

и имеем

AV1 = λ1V1 , AVi1 = λiVi1 +Vi2 , AVi2 = λiVi2 +Vi3 ,

	AVim	= λiVim .
	i	i
Отметим, что	Bi = λi I +u ,
где
0
	0	0
1
	1	.
u =
		.
		.
0		10

и

163

k

k

k

k −1

k

k −2

2

k

Bi

= λi

I +

λi

u +

λi

u

+…+u

,

1

1

где uk – нулевая матрица, если k ≥ n , а если сдвинутая вниз на каждую дополнительную степень

k > n – диагональ единиц в u , u . Например,

													0	0		… 0		0	0
														0		… 0		0
													0						0
													u2 = 1 0 … 0					0	0 .
														1		… 0		0
													0						0
														0		… 1		0
													0						0
		Теперь пусть
												e = a1V1 + a21V21 + a22V22 +…+ a2m2V2m2 + a31V31 +…+ ar mrVr mr ,
														r	mr		j	k		−lVij ,
												Ak e = a1λ1kV1 +∑∑∑aij							λik
														i=2 j=1 i=0				j −l
								Ak				= c1λ1k + p2,k λ2k + p2,k −1λ2k −1 +…+ p2,1λ2 +…+ prk λrk +…+ pr,1λr +c2 ,
		где pij – полиномы от k , а c1 , c2												– постоянные, не зависимые от k . Выражение
	Ak e
					, будет иметь член
	Ak													a λkV
															1	1	1				,
													c1λ1k + p2,k λ2k + p2,k −1λ2k −1 +…+c2

предел которого при k → ∞ будет (a1 c1 )V1 , так как λ1 – единственное наибольшее собственное значение.

Типичный член (i ≥ 2)

ail j k−l λik −1Vij

c1λ1k +…+ pik λik +…+c2

будет стремиться к нулю при k → ∞ (так как λ1 превосходит все другие λ ). Полагая e = (a1 c1 ) и V1 =ω , получаем теорему для A > 0 .

Замечание. Отметим, что c1 = 0 в том и только в том случае, если a1 = 0 . Можно

показать, что a1 ≠ 0 , исходя из того, что все aij	в разложении e и все Vi действи-
тельны и положительны. Малое возмущение e	оставляет a1 ≠ 0 , а результат при
этом останется тем же самым.

Теперь для доказательства теоремы при A ≥ 0 отметим, что из-за aij > 0 сущест-

вует такое положительное целое m , что Am > 0 (т. е. при движении по петлям в конечном счете возможно получение пути любой желаемой длины между произвольной парой вершин соответствующего графа). Приведенное выше доказательство

применимо к Am и его наибольшему собственному вектору ω(Am ). Действительно, так как A – ограниченный линейный оператор (и поэтому непрерывный), имеем

164

	lim	Amk +i	= cω(Am ), 0 ≤ i < m .
		Amk +i
	k →∞

Легко убедиться, что ω(Am ) есть искомый неотрицательный собственный век-

тор.

Это завершает доказательство.

Замечание. Следующая неотрицательная матрица неприводима (ее граф – сильно связный, так как у любой пары вершин имеется путь, связывающий их):

0	2	0
	0
A = 0		4 .
	0
1		0

Эта матрица не удовлетворяет условиям теоремы, поскольку она импримитивна, имея 2 как единственное собственное значение кратности 3. Для пояснения этого

отметим следующее:		Ae = (2, 4, 1)T ; нормализацией получаем			x =	(2 / 7, 4 / 7, 1/ 7)T	;
					1
Ax = (8 / 7, 4 / 7, 2 / 7)T		;	нормализацией	получаем	x =	(4 / 7, 2 / 7, 1/ 7)T	;
1					2
Ax	= (4 / 7, 4 / 7, 4 / 7)T	;	нормализацией	получаем	x = (1/ 3, 1/ 3, 1/ 3)T		;
2					3
Ax	= (2 / 3, 4 / 3, 1/ 3)T	и нормализацией получаем x = (2 / 7, 4 / 7, 1/ 7)T , что то же са-
3				4

мое, что и x1 с зацикливанием вместо сходимости.

7.4. ВЫЧИСЛЕНИЕ СОБСТВЕННОГО ВЕКТОРА

Вычисление главного собственного вектора основано на использовании теоремы 7.13. Она утверждает, что нормализованные строчные суммы степеней примитивной матрицы (и, следовательно, положительной матрицы) в пределе дают искомый собственный вектор. Поэтому краткий вычислительный способ получения данного вектора – возводить матрицу в степени, каждая из которых представляет собой квадрат предыдущей. Строчные суммы вычисляются и нормализуются. Вычисления прекращаются, когда разность между этими суммами в двух последовательных вычислениях меньше заранее заданной величины.

7.5. СОГЛАСОВАННОСТЬ

Обратносимметричные неотрицательные матрицы могут иметь комплексные собственные значения. Следовательно, они не допускают просто общей характеристики. Однако поскольку максимальное собственное значение лежит между наибольшей и наименьшей из строчных сумм, согласованная матрица имеет собственное значение, равное сумме любого из ее столбцов. Как будет показано, малое возмущение не сильно меняет максимальное собственное значение и остальные собственные значения находятся в окрестности нуля, причем их сумма – действительное число.

Выбор возмущения, наиболее соответствующего описанию влияния несогласованности на вычисляемый собственный вектор, зависит от психологического процесса, имеющего место при заполнении матрицы попарных сравнений исходных

165

данных. Предположим, что все возмущения, заслуживающие внимания, могут ( быть сведены к общему виду aij = (ωi ωj )εij . Согласованность имеет место, если εij =1 . Например,

(ωi ωj )+aij = (ωi ωj ) 1+(ωj 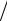ωi )aij .

Теперь получим некоторые элементарные, однако существенные результаты для согласованных матриц. Начнем с выражения

n

λmax = ∑aij (ωj ωi ), j=1

которое является i -й компонентой Aω = λmaxω , и определим

µ= − (n1−1)∑n λi .

i=2

n

Тогда из ∑λi = n следует, что µ = (λmax −n)(n −1); λmax ≡ λ1 , и так как

i=1

λmax −1 = ∑aij

(ωj

ωi ),

j≠i

находим, что

∑

aij (ωj

ωi )+aji (ωi

ωj ) ,

nλmax −n =

1≤i< j≤n

поэтому

λmax −n

1

n

1

µ =

n −1

=

−

+ n(n −1) 1≤∑i< j≤n aij (ωj

ωi )+ aji (ωi ωj ) .

n −1

n −1

Подставляя

aij = (ωi

ωj

)εij ,

εij > 0 , приходам к уравнению

1

µ = −1+ n(n −1) 1≤∑i< j≤n εij +(1 εij ) .

Заметим, что при εij

→1, т. е. при достижении согласованности,

µ → 0 . Кроме

того, µ выпукла по εij , поскольку εij

+(1 εij )

выпукло (и имеет минимум при εij

=1 )

и сумма выпуклых функций выпукла.

Поэтому µ мало или велико в зависимости от

того, близка или далека величина εij

от единицы соответственно (т. е. близки или

далеки мы от согласованности). Наконец, если напишем εij =1+δij ,

то при δij

> −1

имеем

1

2

δij2

µ =

∑ δij

−

.

n

1

+δij

(n −1) 1≤i< j≤n

Теорема 7.14. λmax ≥ n .

Доказательство.

λ −n

1

1≤∑i< j≤n

δij2

max

n −1 =

,

n(n −1)

1+δij

что ≥ 0 , так как

aij

= (ωi ωj )(1+δij ), при δij

> −1 .

166

и рассматривая треугольные контуры, находим

167

aij =1 aji

при δij → 0 .

Теорема 7.15. Положительная обратносимметричная матрица согласована тогда и только тогда, когда λmax = n .

Доказательство. Если A согласованна, то δij = 0 и λmax = n . Наоборот, используя полученный выше результат, отмечаем, что λmax = n , δij = 0 при любом выборе i и

j , следовательно, матрица A – согласованна.

Таким образом, для достижения согласованности желательно, чтобы µ было близко к нулю, или, что то же самое, λmax было близко к своей нижней границе n . Интересно отметить, что (λmax −n)(n −1) можно интерпретировать в терминах ста-

тистической среднеквадратичной ошибки. Действительно, допустим, что δij <1 (и,

следовательно, δij3 (1+δij )) мало по сравнению с δij2 ). Это разумное допущение для «несмещенного» суждения, которое ограничено «естественной» наибольшей нижней границей – 1 для δij (так как aij должно быть больше нуля) и будет стремиться к

симметричной оценке около нуля в интервале (−1, 1). Теперь µ → 0 Умножение на 2 даёт дисперсию δij . Поэтому 2µ и есть эта дисперсия.

Малые возмущения элементов положительной обратносимметричной матрицы вызывают малые возмущения в собственных значениях от их исходной величины. Вообще говоря, это неверно для положительных матриц. Докажем этот факт для

λmax .

Теорема 7.16. Пусть δ = max δij , тогда
i,	j
λmax	−n <	1	∑	δij2 ≤ n −1	δ 2 .
		n	1≤i< j≤n	2

Доказательство очевидно.

Таким образом, если возмущение (или ошибка в суждении) мало, и число сравниваемых элементов также мало (например, менее десяти), то отклонение λmax от n

также мало. Отметим вновь, что для того, чтобы остаться вблизи согласованности, нужно, чтобы n было мало. Например, δ = 0,1 , n = 7 дает λmax −n < 0, 04 , а δ = 0, 9 ,

n = 7 дает λmax −n < 2, 43 .

3амечание. Неотрицательная матрица A = (aij ) с ai, i+1 =1 и aij = 0 – для остальных i , j имеет все собственные значения равными нулю, но та же самая матрица с an1 , замененным на ε , где ε > 0 мало, имеет максимальное собственное значение

λmax = ε1n , которое стремится к единице при увеличении n . Поэтому, хотя λmax из-

меняется непрерывно с коэффициентом ε , ее величина становится большой даже для малых ε (этот факт сообщил мне А. Лауб из Массачусетского технологического института).

В [168] отмечено, что, используя свойство обратной симметричности из равенства aij ajk = aik , имеем aij ajk aki =1. Следовательно, согласованность для обрат-

носимметричной матрицы значит, что все контуры длины три имеют единичную интенсивность.

Предполагая δij <1

aij ajk aki = (1+δij )(1+δjk )(1−δik ) ≈1+δij +δjk −δik ,

n
и, поскольку λmax = ∑εij , имеем ∑ aij ajk aki = n2λmax .
j=1	i, j, k
Для i ≠ j , j ≠ k , i ≠ k	эта сумма становится равной n2 (λmax −n)+n(n −1)(n −2),

так как, подставляя app =1 , apq = aqp−1 , имеем n2 + 2n(n −1) членов, величина кото-

рых равна единице. Усредняя по количеству членов, т. е. n(n −1)(n −2) в результате получаем n(n −2) (λmax −n)(n −1)+1, что справедливо при n ≥ 3 . В любом случае предметом нашего внимания является разность λmax −n .

Теперь проверим гипотезу о согласованности. Полная согласованность может быть сформулирована в виде нулевой гипотезы:

H0 : µ = 0 ,

и мы проверяем ее по отношению к односторонней альтернативе

H1 : µ > 0 .

Соответствующая тестовая статистика будет

m = λmaxn −−1n ,

где λmax – максимальное наблюдаемое собственное значение матрицы, элементы которой aij содержат случайную ошибку. Установление статистической меры для со-

гласованности требует нахождения распределения статистики m . Несмотря на то, что её специфическая форма выходит за рамки материала этой главы, заметим, что m соответствует неотрицательному вероятностному распределению, дисперсия которого есть удвоенное среднее x , и представляется совершенно аналогичным рас-

пределению x2 , если предположить, что все δij , есть N (0, σ )2 на интервале (−1, 1). Для нашей цели при неизвестном распределении используем общепринятое отношение (x − µ0 ) 2x при µ0 = 0 , т. е. используем x2 в качественном тесте для под-

тверждения нулевой гипотезы, когда тестовая статистика, допустим, ≤1 . Поэтому при x > 2 . можно измерять несогласованность.

Более подходящий метод проверки статистики m заключается в используемом нами сравнении ИС с СИ.

Замечание. Заметим, что для матриц A = (aij ), W = (ωi ωj ) имеем

(A −W )ω = (λmax −n)ω ,

откуда видно, что аппроксимация (aij ) посредством (ωi ωj ) тем лучше, чем ближе

λmax к n .

Возвращаясь к представлению

aij =ωi ωj +(ωi ωj )δij ,

находим, что

δij2 = aij (ωi ωj )−1 2 .

168

Таким образом, заменив	a	на ω ω	j	, получим δ2					, сведя тем самым к нулю величи-
ну 2(λmax −n) (n −1).	ij	i						ij
Следовательно, всякий раз, когда						δij		<1 , аппроксимация любого aij величиной

ωi ωj приближает нас к согласованности (см. также обсуждение метода наимень-

ших квадратов, которое будет проведено позже).

Теорема 7.17. Если положительная матрица A согласованна, то каждая строка является положительным кратным любой заданной строки.

Доказательство. Без ограничения общности будем считать, что каждая строка является положительным множителем i -й строки. Из отношения ajk = aik aij следу-

ет, что, зафиксировав j и положив k =1, 2, …, n , j -я строка будет равна i -й строке, умноженной на положительную постоянную (1 aij ).

Замечание. Очевидно, что обратное утверждение этой теоремы неверно. Матрица единичного ранга может и не быть согласованной. Например, в матрице

1 22 4

элемент a21 не равен a11 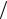a12 .

Таким образом, согласованная матрица при aii =1 имеет следующий общий вид:

ai1 ai1			ai2 ai1	… ain		ai1
ai1		ai2	ai2 ai2	… ain		ai2
	…		…	…	…		.
ai1		ain	ai2 ain	… ain ain

Так как матрица A = (ωi 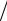ωj ) имеет вид транспонированной по отношению к приведенной матрице, она согласованна.

Теорема 7.18. Если A – положительная и согласованная матрица, то aii =1 и

aij =1 aji .
Доказательство. Из определения следует, что aii	= aij aji и, следовательно, aii =1
для всех i . Также из aii = aij aji следует,, что aij = aii	aji =1 aji .

Теорема 7.19. Положительная матрица A согласованна в том и только в том случае, если она единичного ранга и элементы её главной диагонали равны единице.

Доказательство. Если A согласованна, то aii =1 . Также

aij = a1 j a1i = (1 ai1 )a1 j

и i -я строка есть первая строка, умноженная на (1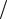a1i ), и, следовательно, ранг A

равен единице. Наоборот, если ранг A равен единице и aii =1 для всех i , то каж-

дая строка является кратной первой строке, т. е.

aij = ci a1 j , ajk = cj a1k , aik = c1a1k , ajj = cj a1 j ,

aij ajk = cicj a1 j a1k = cicj a1 j (aik ci )= cj a1 j aik = ajj aik = aik ,

169

и матрица A согласованна.

Перейдем к иллюстрации понятия согласованности на языке теории графов. Определение 7.3. Интенсивность суждений, относящихся к пуль из i в j (на-

зываемая интенсивностью пути), равна произведению интенсивностей, соответствующих дугам этого пути.

Следующая теорема вносит ясность относительно связи, существующей между интенсивностями путей и согласованностью. Напомним, что перекрывающее дерево

с n вершинами имеет n −1 ребер. Оно является связным графом, включающим все вершины и не имеющим контуров. Поэтому имеется единственный путь между любой парой вершин.

Теорема 7.20. Необходимым и достаточным условием существования единственной положительной согласованной матрицы является то, что объекты (как вершины) и соединяющие их суждения (как дуги) формируют перекрывающее дерево.

Доказательство. Необходимость. Если объекты формируют контур, то имеется не единственный путь между двумя вершинами в контуре, что дает два различных значения для одного и того же элемента. Все объекты должны образовывать дерево, иначе суждения для связывания изолированных объектов были бы произвольными, что нарушило бы единственность матрицы.

Достаточность. Для каждой дуги перекрывающего дерева мы используем интенсивность вдоль единственного пути для получения интенсивностей между объектами

i и j . Это определяет матрицу A = (aij ).

Для доказательства согласованности матрицы A рассмотрим любую строку, на-

пример i -ю. Для любой пары вершин j					и k нужно показать, что ajk , определенная
произведением дуг на пути jk , дана величиной aik						aij , где aik и aij		– соответст-
вующие произведений интенсивностей дуг на путях,						соединяющих i	с	k	и i с j .
Рассмотрим два случая:
1.	i	лежит на пути между j и k . В этом случае ajk				= aji aik = aik aij .
2.	i	не лежит между j и k , тогда:
а)	i ,		j и k	образуют путь; в этом случае путь, определяющий ajk			, дается вели-
чиной		aik	aij ,	если j находится между	i и k и обратной величиной			aij	aik , т. е.
aik aij	,	если k		находится между i и j ,	так как путь должен проходить от				j к k , а
не от k		к	j ;
б)	i ,		j и k образуют вилку в m (см. рис. 7.1). Тогда

ajk = aimamk = ajmami aimamk = ajiaik = aik aij .

Рис. 7.1

Теорема 7.21. Если A – согласованная матрица, то Ak = nk −1 A . Доказательство. Из теоремы Сильвестра имеем

	n	∏(A −λi I )
	f (A)= ∑ f (λi )	j≠i	.
		∏(λi −λj )
	i=1
		j≠i

170