Ответы на экзамен Котюргина / saaty

Aω = λω

Крантц [86] аксиоматизировал альтернативные процессы, связывающие стимулы с суждениями, и получил теоремы существования для шкал отношений. Подобная аксиоматизация не была распространена на иерархии шкал отношений.

Некоторые исследователи подошли к проблеме шкалирования так, как если бы познавательное пространство стимулов было бы по существу многомерным, однако вместо этого мы выбираем иерархическую декомпозицию этой многомерной структуры, чтобы установить количественные, а также качественные отношения между величинами. Отдельные величины в решениях многомерного шкалирования функционально напоминают отдельные собственные векторы на каждом уровне нашей иерархии.

Формально задача построения шкалы в виде нормализованного собственного вектора ω в уравнении (для максимального λ ) подобна выделению первой главной компоненты. Когда экспертов просят заполнить клетки только одной строки или одного столбца, а другие клетки вычисляются по ним (для обеспечения «совершенной согласованности»), первое собственное значение n воспроизводит, 100% изменения матрицы. Если «совершенная согласованность» накладывается на данные за исключением того, что к каждой клетке матрицы добавляется нормально распределенная случайная компонента, то теория приводит к анализу главных факторов, и получится «однофакторное» решение. Следовательно, если совершенная согласованность навязывается экспериментатором, то получается неинтересный результат точного шкалирования, которое было гарантировано, когда эксперимент представлялся в виде одного сравнения. В действительности можно убедиться, что если субъект заполняет только одну строку или столбец матрицы и если задачей субъекта является генерация отношений между парами стимулов, то процедура формально эквивалентна тому, как если бы субъекты располагали каждый стимул вдоль полупрямой с нулём на одном конце: это и есть метод «непосредственной интенсивности» психофизического шкалирования.

Не существует простого взаимоотношения между решением, полученным с помощью собственного значения, и решениями, полученными методом наименьших квадратов, хотя имеются статьи (например, [31, 72, 80]), в которых рассматривается аппроксимация матрицы данных матрицей более низкого ранга, минимизирующей сумму квадратов разностей. В общем случае оба решения одинаковы при наличии согласованности. Общепринятого критерия сравнения не существует. Следовательно, неясно, какой из методов лучше. Повторные применения процедуры нахождения собственного значения помогают достичь согласованности, которая является наиболее предпочтительным для нас критерием.

В [164] предлагается метод «определения параметров функционального отношения посредством факторного анализа». Однако утверждается, что «задача вращения осей остается нерешённой...», т. е. факторный анализ определяет параметры только в пределах линейного преобразования. В [24] обсуждаются методы определения таких преобразований, где априорный теоретический анализ или наблюдаемые величины позволяют сформулировать критерий, по отношению к которому происходит вращение решения относительно произвольного фактора.

Иерархическая композиция является индуктивным обобщением следующей идеи. Заданы веса независимых элементов одного уровня. По отношению к каждому элементу заданного уровня формируется матрица собственных векторов-столбцов элементов уровня, находящегося непосредственно ниже заданного. Затем вектор весов элементов этого уровня используется для взвешивания соответствующих собственных векторов-столбцов. Умножая матрицу собственных векторов на вектор-столбец весов, получаем составной вектор весов элементов нижнего уровня.

Так как матрица собственных векторов не является ортогональным преобразованием, в общем случае результат не может быть интерпретирован как вращение. В действительности, вектор в единичном n -мерном симплексе умножается на стохастическую матрицу. В результате получаем другой вектор в единичном симплексе.

211

Алгебраисты часто указывают на отличие задач, в которых алгебра имеет структурную геометрическую интерпретацию, от задач, в которых она служит удобным методом проведения вычислений. Статистические методы имеют удобную геометрическую интерпретацию в отличие от методов возмущений, которые часто ею не обладают.

Вработе [61] проявлен интерес к поведению экспертов в ситуациях, включающих как линейные, так и нелинейные отношения между стимулами, после чего делается заключение, что процесс индуктивного вывода в основном линейный. В нашей модели реакция экспертов на линейные и нелинейные сигналы кажется адекватно отраженной в описанном в этой книге методе парного шкалирования с привлечением подхода иерархической декомпозиции для агрегирования элементов, попадающих в сравнимые классы в соответствии с возможным диапазоном шкалы сравнений.

Отметим, что мы подходим к решению проблемы интеграции информации, которая обсуждалась в [4], путем формулирования задачи о собственном значении, имеющей линейную структуру. Однако сама шкала, определяемая собственным вектором, является в значительной степени нелинейной функцией данных. Процесс построения собственного вектора включает сложные операции, состоящие из сложения, умножения и усреднения. Чтобы ощутить эту сложность, можно проверить способ получения собственного вектора как предельного решения нормализованных строчных сумм степеней матрицы.

В[4] также акцентируется внимание на том, что принятая шкала реакции должна удовлетворять критерию, который налагает алгебраическая модель суждений. Таким критерием в нашем случае вновь оказывается согласованность.

Наконец, может быть полезным краткое рассмотрение графо-теоретического подхода к согласованности. Направленный граф с n вершинами, который предпола-

гается полным (так как любая пара его вершин соединяется направленной дугой), называется турниром. Его можно использовать для представления доминантных парных сравнений между n объектами, тогда контуры будут представлять нетранзитивность. Например, каждые три вершины определяют треугольник, но не все треугольники образуют 3-контуры. Число контуров заданной длины используется для определения индекса нетранзитивности данного порядка, например тройки или четвёрки. Несогласованность определяется (см. [100]) в зависимости от отношения числа трех, четырех или более контуров в заданном графе к максимальному числу

контуров данного порядка. Для 3-контуров максимальное число будет (n3 −n) 24

для нечетного	n и (n3 −4n) 24 – для четного	n ; для 4-контуров оно будет
(n3 −n)(n −3)	48 для нечетного n и (n3 −4n)(n −3)	48 для четного n . Эти резуль-

таты не были обобщены на k -контуры. Тем не менее среднее число k -контуров для случайной ориентации дуг полного графа – (k −1)!(nk )(12)k . До сих пор не найдена

зависимость между этим определением несогласованности и нашим, относящимся к собственному значению. Непохоже, что зависимость будет найдена. Приведённый выше результат для 3-контуров вместе с его статистическими следствиями принадлежит Кендаллу. Он подробно обсуждается в обычной статистической справочной литературе (см., например, [108]).

Выше мы ссылались на анализ главных компонент. Обсудим кратко эту процеду-

ру.

Рассмотрим случайный вектор X с p компонентами, вектор с нулевым средним и ковариационной матрицей C . Распределение X неизвестно. Пусть b есть p -

212

bT b1 = 0

0 = E (bT Xb1T X )= E (bT XX T b1 )= bT Cb1 = λmaxbT b1 .

b1T X

λmax .

компонентный вектор-столбец, bT b =1; тогда E (bT X )2 = E (bT XX T b)= bT Cb обозначает операцию математического ожидания.

Нормализованные линейные комбинации bT X с максимальной дисперсией при условии bT b =1 получаются из функции Лагранжа, определенной в виде

bT Cb = λ(bT b −1),

где λ – множитель Лагранжа.

Приравнивая производную по b нулю, получаем уравнение

(C −λI )b = O ,

нетривиальным решением которого будет λ – собственное значение C .

Если умножить эти выражения на bT и использовать условие ограничения, то получим bT Cb = λbT b = λ . Это показывает, что λ является дисперсией величины bT X . Поэтому в качестве максимальной дисперсии нам следует использовать Если нормализовать соответствующее решение b1 , разделив его на сумму квадратов

коэффициентов, то получим в качестве нормализованной линейной комбинаций с максимальной дисперсией. Затем получаем новую нормализованную комбинацию bT X с максимальной дисперсией всех линейных комбинаций, некоррелированных с bT X , т. е.

Однако	Cb	= λ	b	и, следовательно,	bT X ортогонально к	bT	X . Используя
	max	max	1			max

в качестве нового ограничения, образуем новую функцию Лагранжа.

bT Cb =α (bT b −1)−2β (bT Cb1 )

смножителями Лагранжа α и β . Действуя таким образом, можно показать, что

β= 0 и α будет вторым наибольшим собственным значением C . (Отметим, что по-

скольку C как ковариационная матрица симметрична, все её собственные значения деиствительны). Действуя как и прежде, теперь получим соответствующий собст-

венный вектор при условии, что bT X имеет максимальные дисперсии из всех нормализованных линейных комбинаций, не коррелированных с b1T X и b2T X и т. д.

Когда собственные векторы получены таким образом, отношение каждого собственного значения ко всей сумме собственных значений представляет долю всей дисперсии, отраженную в соответствующих компонентах. Поэтому первым (и практически важным) приближением считают главную компоненту и ищут изменения в

условиях, ведущих к изменениям в выражении b1T X .

В [115] сделана попытка определить влияние отдельных журналов, проверяя число цитирований. Устанавливается матрица цитирования числа статей из каждого журнала, упомянутого в каждом источнике. Столбцы затем нормализуются, чтобы принять во внимание различные размеры журналов. Далее следует вычисление весов влияние в соответствии с разработанной ими процедурой нахождения собственного вектора общей матрицы (которая не ориентирована на шкалу отношений).

213

9.5. ПОДХОД, ОСНОВАННЫЙ НА ВОЗМУЩЕНИЯХ: МЕТОД ЛОГАРИФМИЧЕСКИХ НАИМЕНЬШИХ КВАДРАТОВ

В случае несогласованности задачу можно поставить следующим образом: определить такие ω1, ω2 , …, ωn , чтобы

aij − fij (ωi , ωj ; αi , αj ;…, ωi , ωj )=	ωi		gij ( ),
	ω	j

где для параметров возмущения имеем

lim gij ( )=1.

Здесь аргумент в gij ( ) включает те же самые переменные и параметры, что и fij . Отметим, например, что мультипликативный параметр следует устремить к единице, а аддитивный параметр – к нулю. Другими словами, если есть надежда вос-

становить хорошие оценки ωi

ωj

из aij

, то возмущения должны быть малы. Отме-

тим, например, что

αiωi +ωi

= ωi

αi

1+ωi

αiωi

a =

(9.1)

α ω

ij

α

j

ω

j

+ω

j

ω

j

α

j

1

+ω

i

i i

Можно зависать (9.1) в виде

aijωj

ωi = gij .

(9.2)

Это основная, недоопределённая система

n2

уравнений с n2 + n

переменными

ωj и gij , требуется n дополнительных уравнений относительно gij ,

чтобы система

стала разрешимой. Выбор этих отношений может быть свободным. Тем не менее оказывается, что эти n отношений могут быть получены, если основываться на выходе, связанном с возмущением рассмотренного выше идеального случая. Исходя из соображений о генераторе бесконечно малых величин требуем, чтобы следующая система соотношений всегда выполнялась:

n
∑gij	= λmax , i =1, …, n ,
j=1
и множество этих условий зависит от A = (aij ).
Задача 1: Найти ωi , i =1, …, n , которые удовлетворяют
n
∑aijωj	=αmaxωi , i =1, …, n .	(9.3)

j=1

Системы соотношений (9.2), а также (9.3), часто используются в качестве необходимых условий, возникающих при решении задачи оптимизации. Например, (9.2)

можно записать в виде log aij (ωj ωi )= log gij ; возводя в квадрат обе стороны этого равенства и суммируя по i и j , получим задачу минимизации ошибки относительно

ωi , i =1, …, n .

Задача 2 заключается в нахождении ωi , которые минимизируют

n	log aij −log (ωj	ωi ) 2	n	(log gij )2 .
∑			= ∑
i, j=1			i, j=1

Это – задача логарифмических наименьших квадратов. Однако она имеет точно такое же решение

214

	n	1/ n n		1/ n		n	1/ n
ωi = ∏aij			∑ωj		= ∏aij			, если
	j=1		j=1			j=1

которое получается при рассмотрении произведения по

n

условии ∑gij =1 – системы n условий, не зависимых от

j=1

aji =1 aij ,

j в обеих частях (9.2) при

A = (aij ). Это решение мо-

жет быть интерпретировано как решение, порождающее ближайшую согласованную матрицу к заданной матрице в смысле логарифмических наименьших квадратов.

В статистике анализ главных компонент использует систему (9.3) в качестве необходимых условий для задачи оптимизации следующего типа. Минимизировать квадратическую форму

n

f (ω1, …, ωn )= ∑aijωiωj , aji = aij , i, j=1

при условии

g(ω1, …, ωn )= ∑ωi2 =1.

i=1n

Лагранжиан этой задачи будет

L(ω1, …, ωn ; λ)≡ f −λ(g −1).

Параметр λ появляется в задаче как множитель Лагранжа (который также является параметром возмущения в задаче оптимизации), а не как собственно параметр, как в (9.3). Действительно, можно построить широкий класс задач оптимизации, используя (9.2) или (9.3) в качестве системы необходимых условий.

Полезно взять уравнения возмущений (9.2) и создать таблицу условий, налагаемых на различные методы вместе с соответствующими решениями. Назовём левый собственный вектор, который является решением задачи, сформулированной в терминах гармонического среднего, вектором антиприоритетов. Он представляет меру того, насколько элемент доминируется другими элементами того же уровня. Соответствующий вектор, полученный посредством иерархической композиции, измеряет воздействие иерархии на каждый элемент уровня (см. табл. 9.1).

Замечание. Решения задачи логарифмических наименьших квадратов, связанной с двумя матрицами оптического примера из гл. 2, будут (0,61; 0,24; 0,10; 0,05)

и (0,61; 0,23; 0,10; 0,06).

Если связать арифметические, геометрические и гармонические средние в нашей задаче шкалирования, то табл. 9.1 легко объясняется.

215

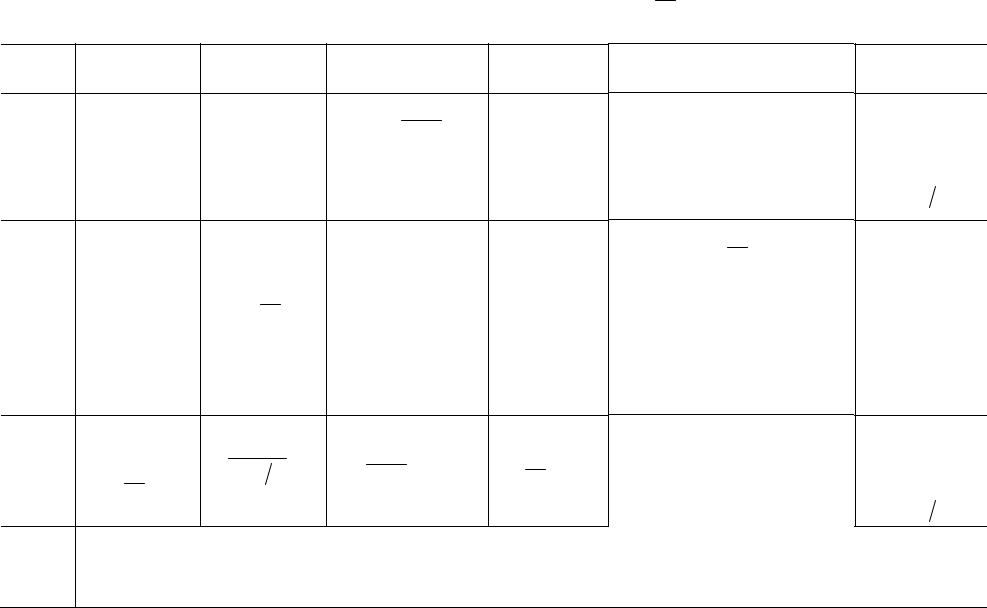
Таблица 9.1. Четыре метода возмущений при a ωj

= g

ij

ij ω

i

Предположения

Предположения

в случае согла-

Задача

Решение

Задача

Решение

в общем случае

сованности

n

ω

ω =

aij

n

Нормализован-

gij =1,

∑aij

= n ,

,

ωi

ный правый соб-

Арифме-

i

i

n

n

∑aij

= λmax ,

тическое

n

j=1

ωj

∑aij

∑gij = λmax ,

ωj

ственный вектор;

∑gij

= n

i =1, …, n ,

i=1

j=1

j=1

индекс согласо-

среднее

n

j =1, …, n

Aω = λmaxω

ванности

j=1

Aω = nω

∑ωi =1

(λmax −n) (n −1)

i=1

n

∏aij ωj = µ

j=1

ω

i

Средне-

gij =1,

n

ω

Обычно заменяется на критерий

То же, что и в

геомет-

n

∏aij

j

=1 ,

1/ n

n

логарифмических средних квад-

случае согласо-

рическое

ωi

∏gij = µ

ратов:

ванности; не

∏gij

=1

j=1

ωi = (naij )

по стро-

i =1, …, n

j=1

n

ω

2

имеется меры

кам

j=1

−log

=

согласованности

min ∑

log aij

ω

i

i, j=1

j

min log2 µ

n

Нормализован-

gij =1,

n

1

∑aij

n

n

ный левый собст-

Гармони-

∑i=1

венный вектор;

n

1

a u

u

= n ,

ui

= i=1

,

∑ui =1

∑ 1 = λmax

uA = λmaxu

ческое

j

индекс согласо-

среднее

∑

gij

= n

ij

i

aij

i=1

j=1 gij

ванности

uA = nu

j=1

(обратное первому

(λmax −n) (n −1)

случаю наверху)

Средне-

геомет-

То же, что и для среднегеометрического по строчкам

рическое

по таб-

лицам

216

9.6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ АППРОКСИМАЦИИ МАТРИЦЫ МАТРИЦЕЙ МЕНЬШЕГО РАНГА

Матрица W = (ωi ωj ) ранга один получается после решения задачи о собствен-

ном значении. Она является приближением к матрице A = (aij ). Мы используем тот

факт, что любая матрица может быть аппроксимирована другой матрицей меньшего ранга. Это делается следующим образом. Во-первых, отметим, что

n

tr (AAT )= ∑aij2 ,

i, j=1

n

tr (A −W )(A −W )T = ∑ aij −ωi ωj 2 ,

i, j=1

min tr (A −W )(A −W )T		n
		= min ∑αi ,
		i=1
где αi – собственные значения матрицы (A −W )(A −W )T .
Теперь для любой матрицы X матрица	XX T	симметрична, и все ее собственные
значения действительны. Кроме того, X и	X T	положительны. Поэтому XX T поло-

жительна и имеет единственное действительное положительное наибольшее собственное значение.

Согласно Джонсону [72]

AAT ≡ PΛPT ,

AT ≡ QΛQT

где Λ – диагональная матрица, элементами которой являются собственные зна-

чения A в порядке убывания величины; собственные векторы матрицы AAT являются соответствующими столбцами матрицы P , а собственные векторы матрицы

AT A – соответствующими строками матрицы QT . Наконец, отметим, что наилучшее

приближение методом наименьших квадратов матрицы A матрицей ранга r может быть задано выражением

Pr Λ1/ 2QrT

где Pr и QrT – части P и QT , соответственно связанные с первыми r столбцами Λ. Пусть r =1, тогда P1 – собственный вектор матрицы AAT , ассоциируемый с мак-

симальным собственным значением; Q1 – собственный вектор матрицы AT A , ассо-

циируемый с максимальным собственным значением. Если, как в согласованном случае,

	Q1		1		1		1
		=		,		, …,		,
		p11			p12		p1n

где

P1 = (p11, p12 , …, p1n ),

то наше решение в согласованном случае будет наилучшим приближением методом наименьших квадратов. Это может быть не так в несогласованном случае.

Проиллюстрируем идею наилучшего приближения методом наименьших квадра-

тов на одной из матриц A примера из оптики, сформировав AAT , AT A и получим их собственные значения и собственные векторы. Собственные значения, одинако-

217

вые для обеих матриц, являются диагональными элементами матрицы Λ, расположенными в порядке убывания. Собственные векторы матрицы AAT совпадают с соответствующими столбцами матрицы P , а матрицы AT A – со строками матрицы QT .

Имеем
	1	4	6	7
		1	3
A =	1/ 4			4		;
		1/ 3	1
	1/ 6			2
	1/ 7	1/ 4	1/ 2	1

132,9000			0
			1, 4710
Λ =							;
	0		0,1283
			0, 0007
	11,528		0
			1, 213
Λ1/ 2 =					;
		0	0,358
			0, 027

			0,875		−0, 475		0, 087 −0, 041
P	=				0, 690		−0,568		0,109
		0, 436									;
			0,188		0,512		0, 669		0,505
		0, 097			0,192		0, 471		0,855
		0, 089			0,349			0,589	0, 723
					0,819			0,146
QT = 0,158									−0,533
					−0,341 0, 767					;
		−0,347							−0, 418
		0,920			−0,303		0, 207		−0,136
			0, 796			3, 034		5,879	7,586
						2,508		2,931	3, 279
PΛ1/ 2QT = 0, 655
				0, 221		1,178		1,554	1,136		.
			0, 099			0,516		0,827	0, 611

Используя подход, при котором находится максимальное собственное значение, получаем вектор в качестве оценки основной шкалы отношений. Основываясь на

методе наименьших квадратов, можно получить матрицу Pr Λ1/r 2Qr пониженного ран-

га (в нашем случае единичного), которая является наилучшим приближением в смысле наименьших квадратов к заданной матрице суждения. Естественно, что эта

матрица является лучшим приближением в смысле наименьших квадратов, чем мат-
рица W = (ωi ωj ), т. е. если определить F = A − Pr Λ1/r	2QrT и G = A −W и просумми-

ровать квадраты их элементов, то можно легко показать, что первая сумма равна tr (FF′)= trΛs , где Λs – диагональная матрица собственных значений, не включен-

ных в Λr (в нашем случае Λr – наибольшее собственное значение матрицы AT A и

218

trΛs – сумма остальных собственных значений). Можно показать, что tr (A −W )T (A −W ) ≥ tr (FF′), как и должно быть на самом деле. Однако задача за-

ключается в получении вектора шкалы из аппроксимированной методом наименьших квадратов матрицы Pr Λ1/r 2QrT . Если предположить, что эта матрица почти согла-

сованна, то можно использовать любой из ее столбцов (нормализованных) как приближение к основной шкале. Но теперь возникает вопрос, насколько хорош этот вектор по сравнению с максимальным собственным вектором. В нашем примере использовалось среднеквадратичное отклонение от известных основных шкал в задачах, где желательно было провести сравнение. Как будет показано в приведенном ниже примере, максимальный собственный вектор явно превосходит вектор, полученный методом наименьших квадратов (как мы его интерпретировали), если его рассматривать как приближение к реальности.

Если образовать Λr , полагая, что все диагональные элементы, кроме первого, наибольшего из них, равны нулю в Λ, то будем иметь

			0,90		3,52	5,94	7, 29
P	Λ1/ 2QT	=			0, 76	2,97	3, 64
			0, 45
r	r r			0,19	0, 76	1, 28	1,57	.
				0,10	0,39	0, 66	0,81
Если сформировать F = A − P Λ1/ 2QT и просуммировать квадраты ее элементов,
	r	r		r r

получается 1,6, но сумма остальных собственных значений trΛs также равна 1,6. Полагая сформированную выше матрицу согласованной, для получения вектора шкалы нормализуем первый столбец и получаем s = (0,548; 0, 274; 0,118; 0, 061). Ин-

тересно отметить, что все другие столбцы дают один и тот же результат, так как матрица единичного ранга.

Хотя этот вектор не является таким хорошим приближением, как собственный вектор, находим, что его среднеквадратичное отклонение от фактического вектора

(0, 61; 0, 22; 0,11; 0, 06)	равно 0,00155, по сравнению с 0,00005 для	максимального
собственного вектора	ω = (0, 62; 0, 22; 0,10; 0, 06), соответствующего	λmax = 4,1. Это

показывает, что для данного примера решение, полученное с помощью собственного вектора, лучше решения методом наименьших квадратов.

Теперь используем элементы ω и s для формирования матрицы отношений W = (ωi ωj ) и S = (si sj ). Затем вычислим A −W и, просуммировав квадраты ее

элементов, получим 13,42. Проделав то же самое для A −S , получим 11,45, что близко к первому результату, однако несколько лучше. Это означает, что аппроксимация методом наименьших квадратов лучше для минимизации суммы квадратов разностей. Для этого примера можно сделать вывод: так как нас интересует шкала, а не матрица отношений, ответ, полученный с помощью собственного вектора – лучше; и это несмотря на то, что он не удовлетворяет критерию минимума квадратов.

219

9.7. МНОГОКРИТЕРИАЛЬНЫЕ МЕТОДЫ

Существуют разнообразные методы для анализа решений при многих целях. Некоторые из них разработаны для прогнозирования действий и выборов в ситуациях принятия решений. Другие разработаны для помощи лицу, принимающему решения, в виде практической техники, которая может быть использована для усовершенствования процедуры принятия решений.

Методы взвешивания

В [152] рассмотрены ранние обзоры по следующим методам оценки весов, приведенным в [151, 13];

1.Взвешивание частных критериев на основе их предсказуемости (с использованием канонической корреляции).

2.Взвешивание частных критериев пропорционально их средней корреляции с другими частными критериями.

3.Взвешивание частных критериев с целью максимизации разности стимулов в величине общего критерия.

4.Взвешивание частных критериев с целью максимизации объясненной дисперсии (с помощью факторного анализа).

5.Взвешивание частных критериев пропорционально их надежности.

6.Равновесное взвешивание частных критериев.

7.Взвешивание частных критериев с целью уравновешивания «эффективных весов» (т. е. долей дисперсии общего критерия).

8.Взвешивание на основе денежного критерия.

9.Взвешивание частных критериев по суждениям экспертов.

10.Взвешивание частных критериев посредством множественной регрессии по построенному в шкале интервалов глобальному критерию.

Эти методы исследуются или критикуются с точки зрения трех основных критериев: релевантности, многомерности и измеримости. Методы 1–7 имеют недостаточную релевантность. Она игнорируется, используются произвольные статистические цели, или релевантность учитывается непрямым и несовершенным образом через другие частные критерии, а не через глобальный критерий. Методы 5–9 содержат смешенную оценку, так как выносится суждение относительно одного частного критерия, а затем независимо относительно другого. Поэтому результирующий многомерный вектор имеет смешение между компонентами, выражающееся подчас в двойном подсчете важности частного критерия. Методы 8–10 страдают сложностью получения мер, которые имеют смысл при взвешивании относительно глобального критерия. Ниже представлены примеры методов взвешивания.

Сопоставление исходов с целями. Допустим, имеются исходы O1, O2 , …, Om .

Этапы процедуры следующие [1, 54]:

1 Ранжировать цели по порядку значений.

2. Присвоить значение 1,00 первой цели и присвоить приемлемые значения другим целям:

цель O1 O2 …Om значение υ1 =1, 00 υ2 …υm .

3. Сравнить наиболее важную цель с совокупностью остальных целей. Короче, сравнить O1 с O2 +…+Om . Если 1 ≥υ2 +…+υm , то сравнить O2 с O3 +…+Om . Если υ2 ≥υ3 +…+υm , то сравнить O3 с O4 +…+Om . и т. д., пока не завершится сравнение

Om−2 с Om−1 +Om .

220