1.Предикаты. Кванторы.

ПРЕДИКАТЫ

ОПРЕДЕЛЕНИЕ

Высказывательной формой или предикатом называется всякое предложение, содержащее наименования неопределенных объектов или неизвестных, которое превращается в высказывание после подстановки в него конкретных объектов вместо имен неопределенных объектов.

Для обозначения неопределенных или произвольных объектов удобно использовать символы переменных. Для каждой такой переменной уточняется множество, элементы которого могут подставляться в высказывательную форму вместо переменной.

Например, к высказывательным формам относится предложение “x учится в школе с номером y“. Здесь x обозначает элементы множества всех людей, а y  элемент множества всех натуральных чисел.

Для удобства будем использовать сокращенную запись высказывательных форм: сначала записывается имя свойства неопределенных объектов, входящих в форму, а затем, в скобках, в определенном порядке перечисляются имена входящих в нее переменных.

Для приведенных примеров высказывательных форм сокращенные записи имеют вид:

Учится(x, y), дружит(x, y), рост-вес(x, y, z), живет (x, y).

Пусть P  это символическое обозначение высказывательной формы (свойства), связывающей компоненты n-элементных наборов объектов, обозначаемых символами переменных x₁, ... , x_n, которые могут принимать значения из множеств A₁, ... , A_n. Тогда предикату P можно поставить в соответствие функцию, отображающую всякий набор из A₁  ...  A_п в одно из двух истинностных значений. Множество A₁  ...  A_п является областью определения соответствующего отображения.

Кроме того множество наборов значений переменных предиката, при подстановке которых вместо неопределенных объектов формы P получается истинное высказывание, образует отношение на множестве всех таких наборов.

Свойство P называется предикатом, а число входящих в него переменных  арностью или размерностью этого предиката.

В частности, высказывания представляют собой нульарные предикаты, поскольку они являются утверждениями, не содержащими переменных.

Общеупотребительные арифметические сравнения могут рассматриваться как бинарные предикаты, которые соответственно можно представлять в виде: Больше(x, у), Больше-или-равно(x, y); Меньше(x, y), Меньше-или-равно(x, y); Равно(x, y), Не-равно(x, y).

Примерами неарифметических предикатов являются предикаты, представляющие родственные связи между людьми. Например, Родитель(x, y), Отец(x, y), Брат(x, y), Родственник(x, y) и другие предикаты.

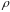
Пусть  некоторое множество наборов вида (a₁, ... , a_n), где a₁, ... , a_n  это элементы множеств A₁, ... , A_n соответственно. Поставим ему в соответствие предикат P(x₁, ... , x_n), принимающий истинностное значение “t“ только на таких наборах значений своих переменных, которые входят в .

Из нескольких разных предикатов можно строить новые предикаты с помощью специальных операций, называемых логическими связками и кванторами.

Основные логические связки  это:

КОНЪЮНКЦИЯ  обозначается как &

(эта связка называется также связкой “И”);

ДИЗЪЮНКЦИЯ  обозначается как

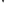
(называется связкой “ИЛИ”);

ИМПЛИКАЦИЯ  обозначается как

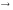
(называется связкой “СЛЕДУЕТ”);

ОТРИЦАНИЕ  обозначается как

(называется связкой “НЕ”).

Если P₁ и P₂  два произвольных предиката, то P₁ & P₂ задает новый предикат, переменными которого являются все различные переменные предикатов P₁ и P₂, а истинностные значения определяются по правилу: P₁ & P₂ принимает значение “t” на тех и только тех наборах значений своих переменных, на которых предикаты P₁ и P₂ являются истинными.

С помощью дизъюнкции образуется предикат, обозначаемый P ₁ P ₂, принимающий значение “t” на тех и только тех наборах значений переменных, на которых хотя бы один из предикатов P₁ и P₂ принимает значение “t”. Соответственно предикат P₁ 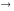P₂ принимает значение “t“ всегда за исключением случая, когда P₁ истинен, а P₂ ложен.

Наконец, отрицание  это операция, применяемая к произвольному предикату P, которая имеет результатом новый предикат P, истинный только тогда, когда P ложен.

Кроме логических связок к предикатам применяются еще две специальные операции, называемые кванторами существования и всеобщности, которые обозначаются символами 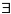и .

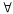Квантор существования

Пусть P(x₁, ... , x_n)  некоторый предикат. Тогда применение квантора существования по переменной x_i этого предиката к P(x₁, ... , x_n) записывается как  x_i P(x₁, ... , x_n). Эта запись представляет новый предикат B(x₁ ,.., x_i-1, x_i+1, _... , x_n), переменными которого являются все переменные P за исключением x_i. Логическое значение предиката B для любого конкретного набора значений переменных этого предиката определяется по следующему правилу. Если существует такое значение переменной x_i, для которого логическое значение P равно "t", то B на наборе является истинным.

Если такого значения переменной x _i не существует, то значение B на наборе является ложным.

Квантор всеобщности

Применение квантора всеобщности переменной x_i к предикату P(x₁, ... , x_n) записывается как:x_i P(x₁, ... , x_n). Эта запись представляет новый предикат B(x₁, ... , x_i-1, x_i+1, …, x_n). Истинностное значение B для каждого конкретного набора  значений переменных этого предиката определяется по следующему правилу.

Если для каждого значения переменной x_i логическое значение предиката P равно "t", то предикат B на наборе является истинным. В противном случае предикат B на наборе принимает значение "f".

Применение к произвольному предикату любого квантора по некоторой переменной этого предиката приводит к образованию нового предиката, арность которого оказывается на единицу меньше, чем у исходного предиката.

P(x) принимает значение "t" только тогда, когда P(x) принимает значение "t" хотя бы для одного значения переменной x.

Аналогично, предикат  x P(x) принимает значение "t" только тогда, когда предикат P(x) является истинным.

Переменная предиката, к которой применяется квантор, называется связанной переменной. Остальные переменные предиката называются свободными.

2. Комбинаторные правила. Правило птичьих гнезд. Правило сложения.

Комбинаторика занимается изучением свойств конечных конструкций или объектов, составленных по определенным правилам из элементов счетных множеств. Такие объекты будем называть комбинаторными объектами. ОСНОВНЫЕ ПРАВИЛА КОМБИНАТОРИКИ.Существуют три правила, называемые основными комбинаторными правилами, на основе которых могут быть выведены другие специальные комбинаторные соотношения. Они связаны с подсчетом числа комбинаторных объектов, допускающих структурное представление в виде последовательностей или множеств, обладающих простыми свойствами.

Правило птичьих гнезд

Если имеются n + 1 птицы, которых необходимо разместить в n гнездах, то при любом способе размещения хотя бы в одном гнезде окажется не менее двух птиц.

Для обоснования справедливости приведенного правила воспользуемся методом рассуждений от противного. Предположим, что данное правило неверно. Пусть после распределения птиц в каждом гнезде оказалось не более чем по одной птице. Перенумеруем гнёзда, в которые попало по птице натуральными числами 1, . . . , k. Поскольку в гнёзда попало всего k птиц и k  n, то в гнёздах оказались размещены не все птицы. Из получаемого противоречия следует, что предположение о противном неверно, а, значит, верно правило птичьих гнёзд.

Правило сложения

Пусть заданы непересекающиеся конечные множества A₁, ... , A_k. Тогда мощность объединения этих множеств может быть определена по формуле:

| | = .

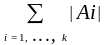Для обоснования справедливости правила сложения заметим, что в значении левой части записи правила каждый элемент объединения непересекающихся множеств A₁, . . . , A_k учтен ровно один раз. Значение в правой части правила учитывает все элементы каждого из множеств A₁, . . . , A_k. Поскольку последние множества непересекающиеся, то всякий элемент их объединения учитывается в правом значении также ровно один раз. Это означает справедливость правила сложения.

3. Правило умножения.

Пусть необходимо строить все возможные nэлементные последовательности a₁, ... , a_n, для которых выполнены условия:

a) первый элемент таких последовательностей может быть выбран m₁ способами;

b) если i < n, то для каждого способа выбора значений первых i элементов последовательности значение i+1-го элемента таких последовательностей может быть выбрано m_i+1 способами.

Тогда число различных последовательностей a₁, . . . , a_n равно:

m₁ m₂ . . . m _n.

Обосновать справедливость правила умножения можно, например, математической индукцией по значению n.

Базис индукции

n=1

Количество одноэлементных последовательностей a₁ принимает m₁ разных значений.

Индуктивное предположение

n = k

Пусть количество различных последовательностей, удовлетворяющих условиям правила умножения, равно m₁ m₂ ... m_k.

Индуктивный переход

n = k + 1.

Последовательность (a₁,a₂,…a_k,a_k+1) для которой выполняется условие правила умножения, тогда эти же условия выполняются и для начала выполняемой последовательности длины л (а₁, а₂,…,a_k)=> существуют ровно m₁,m₂…m_k разных начал последовательности (a₁,a₂,…a_k).

Каждое такое начало длины k при дописывании еще одного элемента a_k+1 порождает m_k+1 разных последовательностей длины k+1.

Поэтому число последовательностей длины k+1 в m_k+1 больше раз начала таких последовательностей длины k => количество таких последовательностей равно m₁ m₂ … m_k m_k+1.

4.Размещения с повторениями и без.

Пусть D  конечное множество, содержащее n элементов.

ОПРЕДЕЛЕНИЕ

Размещениями из n элементов по m элементов множества D называются m-элементные последовательности, каждый член которых является элементом D.

Здесь предполагается, что m  0. При этом, если m = 0, то соответствующее размещение не содержит ни одного элемента и является пустым.

Если множество D неизвестно или не уточняется, то говорят о размещениях из n по m.

Например, слово FALKON может рассматриваться как размещение из 26 элементов символов английского алфавита по 6.

Размещение называется размещением без повторений, если все входящие в него элементы являются разными.

Заметим, что для размещений с повторениями должно выполняться условие m n, так как в противном случае по правилу птичьих гнезд в размещении, длина которого больше числа элементов множества, из которого выбираются элементы размещения, будет повторяться хотя бы один символ.

Размещение, в котором могут встречаться одинаковые элементы, называется размещением с повторениями. Из приведенных определений следует, что всякое размещение без повторений одновременно является и размещением с повторениями.

Размещения используются для представления таких комбинаторных объектов, каждому элементу которых должно быть сопоставлено свойство, отличающее его любого из остальных элементов в составе объекта.

Определим число различных размещений из n по m без повторений. В таких размещениях первый элемент может быть выбран n способами, при всяком способе выбора первого элемента выбор второго элемента может быть осуществлен n1 разными способами и т.д. При всяком способе выбора значений первых m 1 элементов последний mй элемент может быть выбран n  m + 1 способом.

По правилу умножения число таких размещений не зависит от множества A и равно значению произведения:

n  (n  1)  ...  (n  m + 1).

Для обозначения число размещений без повторений из n по m применяется специальное выражение . Поэтому: = .

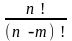В размещениях из n по m с повторениями каждый элемент такого размещения может быть выбран n способами. Поэтому по правилу умножения число размещений с повторениями из n по m равно .

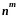Число размещений с повторениями обозначается как 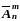. Следовательно, справедливо соотношение: = .

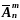Частным случаем размещений без повторений являются размещения всех элементов множества или перестановки элементов множества. Как следует из приведенных формул число P_n перестановок элементов произвольного n элементного множества равно n

5.Сочетания без повторений.

ОПРЕДЕЛЕНИЕ

Сочетанием из n элементов по m элементов n-элементного множества D называется всякая совокупность, состоящая из m элементов D.

Если множество D неизвестно или не уточняется, то говорят о размещениях из n по m.

Так же, как и для размещений, предполагается, что m  0. Если m = 0, то такое сочетание не содержит элементов, т.е. является пустым множеством.

Как следует из приведенного определения в сочетаниях, в отличие от размещений, важен только состав входящих в них элементов, которые в составе сочетания не различаются между собой.

Сочетания могут быть с повторениями и без них.

В сочетании без повторений все элементы совокупности являются разными. Для существования таких сочетаний необходимо выполнение дополнительного условия n  m. Всякое такое сочетание может рассматриваться как подмножество того множества, из которого выбираются элементы сочетания. Поэтому множества всех сочетаний без повторений некоторого конечного множества и множество подмножеств этого множества равны.

Из приведенных определений следует, что в сочетании с повторениями могут содержаться одинаковые элементы. Поэтому сочетания без повторений одновременно являются и сочетаниями с повторениями.

1.Число сочетаний без повторений из n по m.

Пусть D это некоторое множество, состоящее из n элементов. Рассмотрим все размещения без повторений из n по m, составленные из элементов этого множества. Число таких размещений равно .

Компоненты каждого такого размещения определяют некоторое сочетание без повторений из n по m, составленное из элементов этого размещения. При этом размещения, отличающиеся лишь порядком вхождения значений, образуют одно и то же сочетание.

Поскольку размещения, соответствующие одному и тому же сочетанию являются перестановками элементов этого сочетания, то всякое сочетание порождается m! различными размещениями. Обозначим число сочетаний из n по m без повторений как .

Поэтому имеет место равенство m! = .

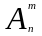Следовательно, справедлива следующая формула для числа сочетаний без повторений: = .

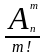Пусть D  это произвольное множество, содержащее n элементов. Тогда число mэлементных подмножеств этого множества равно . Значит число всех различных подмножеств данного множества равно + + ... + .

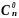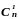С другой стороны, поскольку число подмножеств nэлементного множества равно 2ⁿ, то для сочетаний без повторений справедливо равенство:

+ + ... + = 2ⁿ.

6.Сочетания с повторениями. Разбиение множеств на части.

Число сочетаний с повторениями из n по m .

Пусть D = {a₁, ... , a_n}  некоторое множество. Сочетания с повторениями, содержащие по m элементов этого множества, будем представлять двоичными последовательностями длины n + m  1, составленными из m нулей и n  1 единиц.

Двоичная последовательность, сопоставляемая отдельному сочетанию, состоит из n групп последовательно идущих нулей разделенных, n  1 единицами.

В i-й группе нулей, отсчитываемой слева направо, столько нулей, сколько экземпляров элемента a_i входит в выбранное сочетание. Если некоторый элемент не входит в сочетание без повторений ни одного раза, то соответствующая ему группа нулей окажется пустой.

Например, если A = {a₁, a₂, a₃, a₄}, то сочетание с повторениями, содержащее 2 элемента a₁, 3 элемента a₂ и 2 элемента a₄ представляется двоичным набором:

(0 0 1 0 0 0 1 1 0 0).

Покажем, что определенное ранее соотношение между сочетаниями с повторениями из n по m и двоичными последовательностями длины n + m  1, содержащими по m нулей, является биективным.

Всякая двоичная последовательность длины n + m  1, содержащая m нулей, разбивается входящими в неё единицами на n последовательно идущих групп нулей, определяющих количества вхождений элементов a₁, ... , a_n в m элементное сочетание с повторениями. Следовательно, соотношение сочетаний с повторениями и двоичных последовательностей является сюрьективным.

Покажем, что если  = ₁, . . . , _m+n1 и  = ₁, . . . , _m+n1  две разные двоичные последовательности, то они представляют разные сочетания с повторениями. Пусть V₁, . . . , V_n и W₁, . . . , W_n  последовательности групп нулей разделенных единицами в последовательностях  и . Тогда найдется такое i, что V_i  W_i. В противном случае  и  оказываются равными. Следовательно, соотношение сочетаний с повторениями и двоичных последовательностей является инъективным.

Поэтому, число сочетаний с повторениями из n по m равно числу рассматриваемых двоичных последовательностей.

Легко проверить, что последних ровно столько, сколько имеется различных способов выбора из n + m  1 позиций в двоичных последовательностях, таких n  1 позиций, в которые записываются единицы. В каждом случае остальные позиции последовательности заполняются нулями.

Число способов выбора различных n  1 позиций, если имеется n + m 1 разных позиций, равно: .

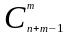Для обозначения числа сочетаний с повторениями из n по m применяется запись 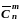. Поэтому справедлива формула:

= _.

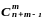РАЗБИЕНИЯ МНОЖЕСТВ НА ЧАСТИ

Пусть задано множество S = {a₁, ... , a_n}. Требуется распределить элементы S по k именованным множествам S₁, ... , S_k так чтобы в S₁ попало n₁ элементов, в S₂  n₂ элементов, . . . , в S_k  n_k элементов множества S. При этом всякий элемент множества S попадает лишь в одно из множеств S₁, ... , S_k.

Поэтому справедливы соотношения:

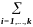S = S_i и n = |S_i |.

Такое распределение элементов S среди множеств S₁, ... , S_k называется разбиением S на части, имеющие заданные мощности. При этом множества, на которые разбивается S, являются именованными, то есть различаются не только по составу, но и по именам. Поэтому в задаче разбиения S на части важно не только выделение систем подмножеств с заданными мощностями, на которые распадается исходное множество, но и то какие множества образуют какие части.

Рассмотрим несколько примеров задач, приводящих к разбиениям множеств на части.

1. Имеется 15 разных картин, которые требуется разместить в трех залах музея так, чтобы в первом зале было выставлено 6 картин, во втором  5 картин, в третьем  4 картины.

Всякое распределение картин по залам, с выполнением сформулированных условий, является разбиением множества из 15 картин на три части, мощности которых равны соответственно 6, 5, 4.

2. Требуется распределить 20 заданий поровну между пятью служащими.

Любое распределение заданий представляет собой разбиение множества всех заданий на 5 подмножеств, каждое из которых содержит четыре элемента.

Выведем формулу для нахождения числа различных разбиений конечного множества на части.

Пусть задано множество S = {a₁, ... , a_n}, которое требуется разбить на k подмножеств S₁, ... , S_k, содержащих соответственно по n₁, . . . , n_k элементов.

Возьмем произвольную перестановку a_i1, . . . , a_in элементов S. Для этой перестановки определим разбиение S на части, полагая, что первые n₁ элементов в ней образуют множество S₁, следующие за ними n₂ элементов перестановки образуют S₂ и т.д. Последние n_k элементов перестановки образуют множество S_k. Приведённое правило определяет отображение множества перестановок элементов S во множество разбиений S на части.

Определим свойства этого отображения.

Пусть множества S₁, ... , S_k образуют разбиение S на части с заданными количествами элементов в них. Тогда всякое размещение без повторений всех элементов S, получаемое выписыванием без повторений сначала всех элементов S₁, затем всех элементов S₂ и т.д., пока не будут выписаны без повторений все элементы множества S_k, образует перестановку элементов S. Такая перестановка отображается в исходное разбиение S₁, ... , S_k. Поэтому отображение перестановок множества S в разбиения S является сюрьективным.

Число перестановок, порождающих одно и то же разбиение множества S на части равно количеству последовательностей, составленных из перестановок элементов множеств S₁, ... , S_k, то есть определяется выражением: n₁! ... n_k!.

Поскольку всего существует n! перестановок элементов A, и каждому разбиению S соответствует n₁! ... n_k! таких перестановок то число различных разбиений S на части S₁, . . . , S_k равно

.

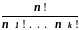Применение последней формулы к приведенному ранее примеру задачи на распределение картин по трем залам музея позволяет утверждать, что существует ровно 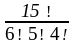вариантов такого распределения.

7. Отношения. Представление и свойства отношений.

ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ ОТНОШЕНИЙ

Пусть заданы множества А и B. Бинарным отношением на этих множествах (или отношением) называется всякое подмножество множества А  B. Тo есть отношение на А и B  это произвольное множество пар элементов, первая компонента которых принадлежит А, а вторая - множеству B.

Содержательно всякое отношение состоит из таких пар элементов, между которыми существует определенная смысловая связь. Для обозначения отношений в дальнейшем будут использоваться строчные символы греческого алфавита:

Если (a, b) , то в этом случае говорят, что элементы a и b находятся между собой в отношении .

Для записи факта, что элементы a и b находятся между собой в отношении , используется также запись a  b.

Одним из свойств бинарных отношений на произвольных множествах А и B является возможность взаимно однозначного соответствия между такими отношениями и бинарными предикатами, переменные которых принимают значения из множеств А и B соответственно.

Такое соответствие предикатов и отношений определяется следующими соотношениями.

1. Пусть   А B. Ему соответствует такой предикат P(x, y), для которого переменные x и y принимают значения на множествах A и B, что P(x, y) является истинным для тех и только тех наборов значений переменных x и y, которые входят в отношение .

2. Пусть P(x, y)  некоторый предикат, переменные которого принимают значения из множеств A и B соответственно. Этому предикату можно сопоставить отношение   А  B, состоящее из тех и только тех элементов множества А B, на которых предикат P является истинным.

Понятие отношения обобщает понятие отображения.

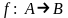
Если  некоторое отображение, то ему можно поставить в соответствие отношение . Такое отношение  принято называть графиком отображения f.

Если отношение  образует график некоторого отображения, то для него справедливо следующее свойство. Для каждого элемента x A в отношении  содержится ровно одна пара, первая компонента которой равна x.

ПРЕДСТАВЛЕНИЕ ОТНОШЕНИЙ

Возможны несколько специальных способов задания отношений.

Представление отношений диаграммами

Пусть   А B. Это отношение между элементами множеств А и B. Если множества A и B счетные, то их можно представить на плоскости множествами точек из двух непересекающихся областей, обозначаемых как A и B. Если (a, b) , то точки, соответствующие a и b, соединяются ориентированной дугой. Такое представление аналогично диаграммам для отображений. При этом для диаграмм отношений допускается как многозначность связи элементов A с элементами B, так и отсутствие связей.

Табличное задание отношений

Если множества A и B являются конечными и A = {a₁,..., a_m}, B= {b₁, ... , b_n}, то всякое отношение   А B можно представить таблицей, состоящей из m строк и n столбцов, имеющей следующий вид:

	b1 bj bn
a1 ai am	. . . . . . . . i,j . . . . . . . . .

В этой таблице значение всякого элемента _i,_j определяется соотношением:

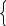1, если (a_i, b_j)

_i,_j =

0, если (a_i, b_j).

Всякая заполненная нулями и единицами таблица, состоящая из m строк и n столбцов, представляет некоторое отношение на множествах A и B, составленное из всех таких пар (a_i, b_j), для которых _i,_j = 1.

Определенное соотношение таблиц и отношений на множествах является биективным. Табличное представление отношений удобно для программной реализации алгоритмов решения задач, связанных с отношениями.

БИНАРНЫЕ ОТНОШЕНИЯ НА МНОЖЕСТВЕ

Отношение А А называется отношением на A. Такие отношения называются также бинарными отношениями на множестве A. То есть отношение на A  это отношение между элементами одного и того же множества A.

Для таких отношений можно выделить несколько специальных свойств.

1. Рефлексивность

Отношение А А является рефлексивным, если .

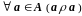Простейшее рефлексивное отношение на A  это множество, состоящее из всех пар вида (a, a), где a A. Такое отношение называется единичным отношением или диагональю и обозначается как .

2. Симметричность

Отношение А А  является симметричным, если  a, b  A (a  b  b  a).

То есть отношение А А симметрично, если для любых a и b из того что (a, b) следует, что пара (b, a) .

Поэтому отношение  несимметрично, если хотя бы для одной пары (a, b) не выполняется указанное свойство. Нетрудно видеть, условие симметричности равносильно условию:

 a, b  A (a  b  b  a).

3. Антисимметричность

Отношение А А антисимметричное, если

 a ,b  A(a  b  b  a  a = b).

То есть отношение А А является антисимметричным, если из (a, b) и (b, a) следует, что a = b.

Заметим, что антисимметричность представляет свойство несимметричности в сильной форме. Отношение антисимметрично, если оно несимметрично всюду за исключением пар из единичного отношения . При этом не требуется, чтобы в антисимметричном отношении содержались все пары, компоненты которых совпадают. Поэтому существуют отношения, которые являются симметричными и антисимметричными одновременно. Такие отношения составлены парами, имеющими равные первую и вторую компоненты.

4. Транзитивность

Отношение А А транзитивное, если

 a, b, c  A(a  b  b  c  a  c).

Отношение А А является транзитивным если из (a, b)  и (b, c)  следует, что (a, c) . Содержательно транзитивность состоит в том, что если осуществляется последовательный многократный переход между элементами множества A, по связям отношения , то между первым и последним элементами такого перехода также выполняется отношение .

8. Отношения эквивалентности. Связь отношений эквивалентности и разбиений на множества.

ОТНОШЕНИЯ ЭКВИВАЛЕНТНОСТИ

ОПРЕДЕЛЕНИЕ

Всякое рефлексивное, симметричное и транзитивное отношение А А, называется отношением эквивалентности.

Если   отношение эквивалентности и a  b, то элементы a и b называются эквивалентными в этом отношении или просто эквивалентными.

Рассмотренное ранее отношение "быть родственником" является отношением эквивалентности. Аналогично, отношением эквивалентности на множестве всех людей является отношение "быть однофамильцем". Это отношение связывает между собой людей с одинаковыми фамилиями, распределяя их по классам людей, каждый из которых состоит из всех людей, имеющих одну и ту же фамилию.

Для представления фундаментального свойства отношений эквивалентности введем понятие разбиения множества.

ОПРЕДЕЛЕНИЕ

Разбиением множества A называется конечное или бесконечное семейство множеств A_i, i  I таких, что:

1) iI(A_i  );

2) i,jI(i 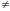j  A_i  A_j = );

3) 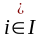A_i = A .

Здесь I это множество значений нижнего индекса множеств разбиения. В разбиениях счетных множеств в качестве множества индексов I обычно применяется все или часть множества натуральных чисел.

Пусть A₁, ... , A_k, . . .  разбиение множества A. Нетрудно проверить, что отношение  на множестве A, определяемое соотношением: a b , является отношением эквивалентности.

Следующая теорема показывает, что справедливо и обратное свойство.

ТЕОРЕМА Всякое отношение эквивалентности на множестве A разбивает это множество на классы эквивалентных элементов.

Доказательство

Разобьем доказательство теоремы на несколько этапов.