14. Монотонные функции

На множестве двоичных наборов длины n определим отношение предшествования наборов.

Пусть и 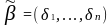. Тогда набор предшествует набору 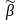, если .

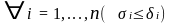Отношение предшествования наборов обозначается как 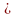, т.е. значение каждой компоненты предшествующего набора не превосходит значения соответствующей компоненты следующего набора.

Например, наборы (0, 1, 0, 0, 1, 0) и (0, 1, 1, 0, 1, 1) находятся в отношении предшествования, а наборы (1, 1, 0, 0, 1, 0) и (1, 0, 1, 0, 1, 1) оказываются несравнимыми в отношении .

Упражнение. Проверить, что отношение предшествования наборов является отношением частичного порядка.

Рассмотрим представление отношения на множестве 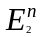с помощью диаграммы для этого отношения, представленной на рис 4.6. Пусть n = 3.

1 1 1

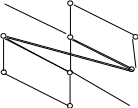
0 1 1 1 0 1 1 1 0

1 0 0 0 1 0 0 0 1

0 0 0

Рис. 4.6

ОПРЕДЕЛЕНИЕ

Булевская функция f(x₁, . . . , x_n) называется монотонной, если для любых наборов и , для которых 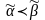, справедливо неравенство .

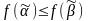Множество всех монотонных булевских функций обозначается как M.

Примеры.

1. Функция f (x₁, x₂)= x₁  x₂ немонотонна, так как

(0, 0) (1, 0), но f(0, 0) > f (1, 0).

2. Функции & и являются монотонными.

Множество всех монотонных функций является замкнутым классом.

Замечание. Доказанное свойство монотонных функций позволяет просто устанавливать монотонность функций, представленных формулами составленными из монотонных функций. Например, монотонной является функция, представляемая формулой

.

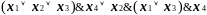Простейшей немонотонной функцией можно считать функцию 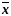, поскольку три остальные функции одной переменной являются монотонными. Покажем, что отрицание (или простейшая немонотонная функция) может быть получено из всякой немонотонной функции. Последнее свойство можно сформулировать иначе: всякая немонотонная функция содержит отрицание, которое может быть выражено из этой функции.

15. Графы. Представление графов. Пути в графах.

ОСНОВНЫЕ ПОНЯТИЯ

Графы – это математическая модель, с помощью которой можно представлять и исследовать формальное описание систем и процессов, состоящих из конечного числа фрагментов или компонент, связанных между собой определенными зависимостями.

Приведем примеры систем, изучение и практическое использование которых связано с представлением в форме конечного числа компонент и связей между ними.

1.Транспортные сети. 2. Молекулы химических соединений. 3. Электронные схемы. 4. Административный аппарат учреждения.

Дополнительно требуется, чтобы выбранные области, представляющие части графа, не имели общих точек, а дуги, отражающие связи, не пересекались и не содержали внутри точек областей, соответствующих частям системы.

Изображение системы, для которой выполнены перечисленные условия, называется геометрической реализацией этой системы.

ОПРЕДЕЛЕНИЕ И СПОСОБЫ ЗАДАНИЯ ГРАФОВ

Графом называется всякая пара G = (V, U), в которой V  это конечное множество, называемое множеством вершин графа, а U  конечное множество ребер графа.

Всякое ребро графа представляется либо одной парой вершин (а,b), либо двумя противоположными парами (a,b) и (b,a). Если ребро из U представляется только одной парой (a, b), то оно называется ориентированным ребром, ведущим из a в b. При этом a называется началом, а b концом такого ребра.

Если ребро u представляется двумя парами (a, b) и (b, a), то u называется неориентированным ребром. Всякое неориентированное ребро между вершинами a и b ведет как из a в b, так и обратно. При этом вершины a и b являются как началами, так и концами этого ребра. Говорят, что ребро ведет как из a в b, так и из b в a.

Всякие две вершины, которые соединяются ребром, называются смежными.

Будем рассматривать только такие графы, у которых все ребра разные и не допускается одновременная связь одной и той же пары вершин ориентированным и неориентированным ребром или парой противоположно ориентированных ребер. Графы, которые допускают возможность нескольких ребер, соединяющих пары вершин, называются мультиграфами.

(В последнем случае соответствующая пара ребер будет рассматриваться как одно неориентированное ребро.)

Тогда ребра графов можно представлять просто парами вершин вида (a, b), для которых дополнительно указывается; является ли ребро ориентированным или нет. В этом случае число ребер графа совпадает с числом пар вершин, которые представляют собой ребра графа.

Поэтому в дальнейшем будем считать, что U  это множество пар вершин. При этом каждое ребро представляется одной парой вершин или двумя парами. То есть, если G = (V, U) и пара (a, b) представляет ребро графа G, то допустима запись (a, b)  U.

Ребро, у которого вершины начала и конца совпадают, называется петлей.

Число ребер, выходящих из некоторой вершины a и отличных от петель, называется степенью этой вершины и обозначается как d(a). Вершина a для которой выполнено равенство d(a) = 0, называется изолированной.

Граф, все ребра которого неориентированные, называется неориентированным графом.

Как уже отмечалось, простейшим способом представления графов является их геометрическая реализация. При этом вершины графов обычно представляются точками пространства, которые помечены обозначениями вершин.

Графы можно изображать так, чтобы дуги, соответствующие ребрам, пересекались. Такое представление графов не является геометрической реализацией, но в некоторых случаях может оказаться полезным или предпочтительным.

Кроме наглядного геометрического изображения и представления графов используются и другие способы задания. Они позволяют представлять графы в виде структур, которые можно хранить и обрабатывать с помощью специальных алгоритмов и программ.

Рассмотрим основные способы заданий графов с помощью специальных структур.