Определение: Элемент a называется наибольшим (наименьшим) в отношении , если  b  a(a  b) ( a  a(b  a)).

Понятно, что всякое упорядоченное множество имеет не более одного наибольшего (наименьшего) элемента. В общем случае упорядоченное множество может не иметь наибольшего или наименьшего элементов. Например, это так для отношения порядка, диаграмма которого приведена на рис 3.2.

a b

c d

e f g Рис. 3.2.

Здесь элементы a и b не являются наибольшими, обладают свойством максимальности для всех тех элементов A, с которыми они находятся в отношении .

ОПРЕДЕЛЕНИЕ: Элемент a называется максимальным (минимальным) в упорядоченном множестве (A, ), если

 b  A(ba  (b, a)) ( bA(ba  (a, b))).

Упорядоченное множество может иметь несколько или не иметь вообще максимальных и минимальных элементов. Например, для упорядоченного множества, представленного диаграммой на рис. 3.2., максимальными являются элементы a и b, а минимальными  e, f и g.

Если A  конечное множество, то любое упорядоченное множество (A, ) всегда имеет максимальные и минимальные элементы. Для бесконечных множеств такое свойство может оказаться неверным.

10.Отношения линейного порядка.

Частным случаем частичного порядка является линейный порядок. Порядок  называется линейным, если:

 a,b A((ba)  (ab)).

То есть, в линейном порядке любые два элемента множества, на котором определено отношение порядка, являются сравнимыми.

Следующая теорема характеризует общий вид диаграмм для отношений линейного порядка.

Теорема 3.3. Если  является отношением линейного порядка на конечном множестве A, то диаграмма для этого отношения имеет вид последовательности, составленной из всех элементов A, в которой всякий предыдущий элемент связан ориентированной дугой со следующим элементом.

Доказательство. Пусть  является отношением линейного порядка на множестве A = {a₁, . . . , a_n}. Проведем доказательство индукцией по мощности множества A.

1. Базис индукции. Пусть A = {a₁}. Тогда диаграмма отношения  на A имеет вид одноэлементной последовательности a₁.

2. Индуктивное предположение. Пусть для каждого множества A содержащего не более чем n элементов выполнено утверждение теоремы.

3. Индуктивный переход. Пусть A = {a₁, . . . , a_n, a_n+1 }.

3.1. Покажем, что  имеет минимальный элемент. Предположим противное. Тогда для отношения  справедливо условие (1):

a  A b A (b  a)   a  A  b A ((a, b)   (b, a) ). (1)

В этом условии левая часть дизъюнкции неверна, поскольку означает существование бесконечной последовательности элементов A, в которой для любых двух соседних элементов a и b выполняется условие b  a, что противоречит условию конечности множества A.

Неверной является и правая часть условия (1). Поскольку в этом случае для отношения линейного порядка найдутся два несравнимых элемента.

Следовательно,  имеет минимальный элемент.

3.2. Покажем что для отношения  выполнено утверждение теоремы. Пусть a  A является минимальным элементом в отношении . Тогда часть этого отношения для множестве A \ { a } является линейным порядком. Если бы это было не так, то несравнимые элементы для части  на множестве A \ { a } оказываются несравнимыми и для отношения  на A.

По индуктивному предположению для A \ { a } выполнено утверждаемое в теореме свойство. Пусть b минимальный элемент для части  на A \ { a }. Тогда диаграмма для части  на множестве A получается из диаграммы для части  на множестве A \ { a }, добавлением ориентированной дуги, соединяющей вершину a с вершиной b.

Доказательство окончено.

Доказанная теорема справедлива для бесконечных множеств, всякое подмножество которого имеет минимальный элемент. При этом отношению  соответствует бесконечная последовательность, имеющая начальный элемент.

11. Логические функции. Задание и элементарные функции.

БУЛЕВСКИЕ ФУНКЦИИ. НАЧАЛЬНЫЕ ПОНЯТИЯ

Пусть E₂ ={0,1}.

Будем рассматривать функции, значения аргумента которых представляют собой двоичные наборы заданной длины, а значения таких функций  элементы множества E ₂.

ОПРЕДЕЛЕНИЕ

Всякое отображение 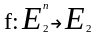, где n  N, называется булевской функцией.

Булевские функции допускают интерпретацию в качестве истинностных функции для предикатов (логических форм) или рассуждений, оперирующих с несколькими факторами, каждый из которых может оказываться как истинным, так и ложным. При этом логическая форма для каждого набора истинных значений таких факторов сама принимает определенное истинное значение.

Если логическая форма U учитывает факторы F₁ ,..., F_n, то функция истинности для значений U в зависимости от значений F₁ ,..., F_n  это некоторая булевская функция .

Множество всех булевских функций обозначается как P₂.

Пусть . Будем использовать символы переменных x₁, . . . , x_n для обозначения первой, второй, . . . , n-й компонент двоичных наборов, являющихся элементами области определения f.

Если задан произвольный двоичный набор (₁,..., _n), то значение _i будет называться значением переменной x_i.

ТАБЛИЧНОЕ ЗАДАНИЕ БУЛЕВСКИХ ФУНКЦИЙ

Естественный способ представления произвольной булевской функции f состоит в явном задании с помощью специальной таблицы, в которой указаны значения f на всех возможных двоичных наборах.

Если , то соответствующая таблица имеет вид:

x1 x2 . . . x n	f(x1 ,. . . , xn)
0 0 . . . 0	f(0 , . . . , 0)
. . .	. . .
1 2 . . . n	f(1, 2, . . , n)
. . .	. . .
1 1 . . . 1	f(1 , . . . , 1)

Приведенная таблица имеет 2ⁿ строк и n +1 столбец. В первых n элементах строк таблицы задаются все возможные наборы значений переменных x₁, . . . , x_n. Поэтому таблица имеет 2ⁿ строк. Последний элемент всякой строки содержит значение функции на наборе значений переменных этой функции, выписанном левее этого элемента в той же строке.

При этом двоичные наборы значений переменных x₁ , . . . , x_n в строках выписываются в порядке возрастания значений двоичных чисел, представляемых этими наборами. Это означает, что для задания произвольной функции f достаточно указать последний столбец табличного задания этой функции. Такой столбец является двоичным набором, содержащим 2ⁿ элементов. Следовательно, многообразие всех возможных функций алгебры логики определяется множеством всех двоичных наборов длины 2ⁿ. Поэтому существует ровно 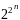различных булевских функций . Множество всех таких б.ф. обозначается как .

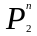ЭЛЕМЕНТАРНЫЕ БУЛЕВСКИЕ ФУНКЦИИ

Табличное задание булевских функций не всегда удобно, поскольку уже для небольшого числа переменных размер таблицы произвольной функции таких переменных оказывается слишком большим.

Рассмотрим способ представления б.ф., в котором одни функции выражаются через другие. При этом некоторые б.ф., называемые элементарными функциями, выбираются в качестве базовых. Они получают собственные обозначения, а остальные функции выражаются через элементарные функции с помощью специальных операций.

Элементарными являются следующие булевские функции.

Функции одной переменной:

1. Тождественный ноль (эта функция обозначается как O(x) или 0).

2. Тождественная единица (обозначается как 1(x) или 1).

3. Отрицание, записываемое как .

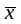4. Тождественная функция (обозначается как I(x) или x).

Табличные задания данных функций имеют следующий вид:

x	0(x)	1(x)		I(x)
0	0	1	1	0
1	0	1	0	1

Функции двух переменных:

1.  (x₁, x₂) - дизъюнкция;

2. & ( x₁, x₂) - конъюнкция;

3.  (x₁, x₂) - импликация;

4. + (x₁, x₂) - сумма по модулю два;

5. ~ (x₁, x₂) - эквивалентность;

6.  (x₁, x₂) - функция Шеффера.

На практике для представления этих функций используется инфиксная запись, в которой символическое имя функции записывается между левой и правой компонентой аргумента, т.е. например, вместо & (x₁, x₂) используется запись: (x₁ & x₂).

Табличные задания этих функций приведены в следующей таблице:

x1 x2	x1 x2	x1& x2	x1 x2	x1+x2	x1~x2	x1 | x2
0 0	0	0	1	0	1	1
0 1	1	0	1	1	0	1
1 0	1	0	0	1	0	1
1 1	1	1	1	0	1	0

Заметим, что отнесение приведенных функций к элементарным достаточно условно. Например, нетрудно проверить, что 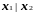совпадает с отрицанием конъюнкции, т.е. одни элементарные функции могут быть выражены через другие такие функции.