13.Минимизация днф.

МИНИМАЛЬНЫЕ ДНФ

Представление б.ф. виде СДНФ в общем случае оказывается не компактнее, чем представление в виде табличного задания, поскольку для каждого набора значений переменных, на котором б.ф. f(x₁, . . . , x_n) равна 1, в СДНФ включается элементарная конъюнкция ранга n. То есть если f принимает значение 1 на значительной части всех наборов, то СДНФ этой функции по размерам сравнима с табличным заданием f.

ОПРЕДЕЛЕНИЕ

Дизъюнктивной нормальной формой (ДНФ) называется всякая формула вида D = K₁ . . . K_r , где K₁, . . . , K_r  это произвольные элементарные конъюнкции.

ОПРЕДЕЛЕНИЕ

Сложностью ДНФ D называется число вхождений в D функций & и . Для обозначения сложности ДНФ используется выражение L(D).

Например, следующая формула является ДНФ:

.

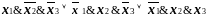Сложность этой ДНФ равна 8.

Одна и та же булевская функция может представляться различными ДНФ.

Например, две ДНФ:

U = 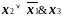и

W = 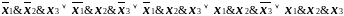представляют одну и ту же б.ф.

Для построения простых схем, получаемых на основе ДНФ, естественно искать такую ДНФ, которая имеет наименьшую сложность среди всех ДНФ, представляющих одну и ту же б.ф.

ОПРЕДЕЛЕНИЕ

ДНФ D, представляющая функцию f, называется минимальной ДНФ для этой функции, если L(D) = min (L(D*)), где минимум берется по всем ДНФ D* , представляющим функцию f.

То есть сложность минимальной ДНФ для f является наименьшей среди сложностей всех ДНФ, представляющих функцию f.

ТЕОРЕМА 4.2. Для каждой б.ф. f, отличной от тождественного нуля, существует минимальная ДНФ.

Доказательство

1. Заметим, что всякая f, отличная от тождественного нуля, представляется хотя бы одной ДНФ (например, это может быть СДНФ).

2. Если задана б.ф. f(x₁, . . . , x_n), то нетрудно проверить, что существует ровно 3ⁿ - 1 конъюнкций разных рангов, составленных только на основе переменных функции f.

Действительно, каждая из переменных f может либо не входить в элементарную конъюнкцию, либо входить в неё без отрицания, либо входить в такую конъюнкцию с отрицанием. Всего таких вариантов для n переменных ровно 3ⁿ. Их них невозможен случай, когда ни одна переменная не входит в элементарную конъюнкцию.

Из 3ⁿ  1 различных конъюнкций с точностью до порядка вхождения элементарных конъюнкций можно составить ровно  1 разных ДНФ.

Действительно, каждая ДНФ задается некоторым непустым подмножеством множества всех конъюнкций.

3. Последовательно просматривая все - 1 ДНФ, составленные из переменных функции f, можно найти такую из них, которая представляет f и имеет минимальную сложность среди всех ДНФ, представляющих f.

Доказательство окончено.

Замечание. Метод нахождения минимальной ДНФ, предложенный в доказательстве теоремы, неприменим на практике, поскольку количество ДНФ, которое требуется проверить для нахождения минимальной ДНФ функции с n переменными, слишком велико. Например, для n = 2 число ДНФ равно 255, а n = 3 число вариантов принимает значение свыше 10⁶. То есть функция числа вариантов, проверяемых ДНФ, слишком быстро растет и для булевских функций, используемых в таких приложениях, как электроника и информатика, оказывается необозримой.

Применяемые на практике методы нахождения минимальных ДНФ или ДНФ, близких по сложности к минимальным, основаны на проведении эквивалентных преобразований ДНФ, представляющих заданную б.ф., в минимальную или близкую к ней с помощью специальных соотношений эквивалентности. При этом в качестве начальной ДНФ можно выбрать СДНФ рассматриваемой функции.

Рассмотрим следующее семейство соотношений эквивалентности.

1. Правила поглощения:

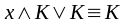и .

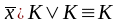2. Правило склеивания: .

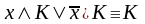3. Правило обобщенного склеивания:

.

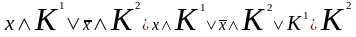Здесь K, K¹, K²  произвольные конъюнкции, или тождественная единица.

Справедливость приведенных эквивалентностей проверяется непосредственно построением таблиц значений формул слева и справа в тождествах 1  3 для различных значений x, K, K¹, K².

В качестве примера применения приведенных правил рассмотрим процесс построения минимальной ДНФ для функции: f = x₁  (x₂  x₃).

Выпишем СДНФ для f:

Применяя правило склеивания к первым трем парам конъюнкций в СДНФ, последнюю формулу можно переписать в виде:

.

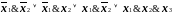Продолжая склеивание подходящих пар конъюнкций пока это возможно, получим формулу: .

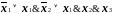Теперь воспользуемся правилом обобщенного склеивания к первой и второй конъюнкциям последней формулы. При этом в качестве K¹ используется пустая конъюнкция  1, а в качестве K²  .

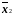В результате получается формула: .

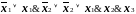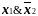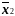К конъюнкциям и применяем правило поглощения. В результате получим формулу: .

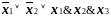Еще два раза последовательно применим правила обобщенного склеивания и поглощения. Сначала для первой и третьей конъюнкций, а затем к тому, что получится, для второй и третьей.

Окончательная формула имеет вид: .

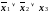Последняя ДНФ минимальна для функции f, поскольку все переменные этой функции являются существенными и каждая переменная должна хотя бы один раз входить в любую ДНФ, представляющую f.