2.5. Магистральная теория.

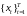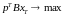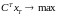Пусть для всех выполняются неравенства , вектор задает начальный запас товаров, – вектор цен на товары. Требуется найти траекторию интенсивностей , такую что , или , где .

Задача

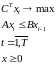. 19019\* MERGEFORMAT (.)

является стандартной задачей ЛП. Однако размерность этой задачи обычно достаточно большая, поэтому решать её сложно с вычислительной точки зрения. Поэтому желательно уметь находить качественные характеристики оптимальной траектории.

Пусть 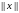– некоторая из норм в 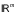. Обозначим

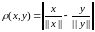, для всех 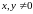, 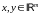. 20020\* MERGEFORMAT (.)

Указанная функция обладает следующими свойствами:

1.  .

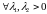
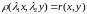2. 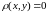 равносильно 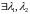: 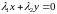– векторы коллинеарны.

3. Если 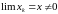, , 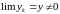то .

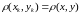Замечание 2.2. Если для всех выполняется 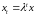, то для всех 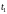и и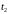меет место 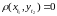, т.е. все состояния стационарной траектории рассматриваются (относительно введенной метрики) как одна точка (именно поэтому название траектории присутствует слово “стационарная”). С точки зрения метрики 020 последовательности векторов и 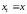неразличимы.

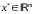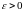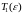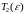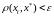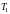Определение 2.4. Говорят, что луч является магистралью для задачи 019, если для каждого найдутся , , такие что для всякой оптимальной траектории выполняется условие для всех , удовлетворяющих условию , причем и 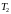не зависят от .

Другими словами, вектор называется магистралью, если любая из оптимальных траекторий идет в направлении этого вектора, исключая, возможно, начальный и конечный периоды (периоды выхода на магистраль и ухода с нее).

Утверждение, устанавливающее наличие магистрали для оптимизационной задачи вида 019 называется теоремой о магистрали.

Определение 2.5. Конической -окрестностью вектора называется множество .

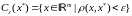Таким образом, вектор является магистралью для задачи 019, если для каждого найдутся , , такие что при всякая оптимальная траектория проходит через окрестность .

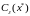Если плановый горизонт достаточно велик (при фиксированном ), то почти всё время оптимальная траектория идет вдоль луча 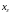, сохраняя почти постоянными пропорции в интенсивности использования различных производственных процессов.

Типичным при этом оказывается такое положение дел, когда луч продолжает оставаться магистралью при широких вариациях вектора С, задающем целевую функцию.

Магистральная теория может быть эффективно использована в тех случаях, когда нет возможности непосредственно вычислить оптимальную траекторию вследствие большой размерности задачи, а также, если нет уверенности в точности выбора целевого функционала. При принятии плановых решений при каждом шаге можно ориентироваться на луч , стараясь заставить все отрасли работать с интенсивностями, пропорции которых близки к пропорциям вектора .

К настоящему моменту существует обширная литература, посвященная изучению магистрального эффекта для различных моделей экономической динамики.

2.6. Теорема о магистрали Моришимы.

Рассмотрим экономику из отраслей, задающуюся матрицей межотраслевого баланса . Для осуществления валового выпуска необходимо произвести производственные затраты 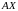. Предлагается, что валовый выпуск 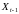предыдущего периода может быть использован как запас сырья в периоде . Получаем задачу:

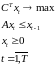, 21021\* MERGEFORMAT (.)

– известный начальный запас.

Обозначим

, , , .

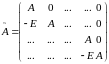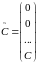где , 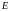, – матрицы . Тогда задача 021 сводится к задаче линейного программирования

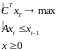. 22022\* MERGEFORMAT (.)

Размерность задачи (матрицы ): .

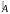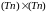Задачу, двойственную к 022, можно записать в виде:

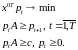23023\* MERGEFORMAT (.)

Определение 2.6. Неотрицательную матрицу A назовем примитивной, если ее векторы Фробениуса образуют одномерное подпространство.

Покажем, что в случае примитивности матрицы вектор Фробениуса является магистралью для задачи 021.

Замечание 2.3. В данном случае векторы Фробениуса матрицы различаются только длиной, все они задают одну и ту же магистраль.

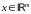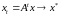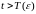Лемма 2.3. Пусть – устойчивая матрица, – ненулевой неотрицательный вектор. Если , то – правый вектор Фробениуса матрицы , причем для каждого найдется , такое что при выполняется условие .

Для доказательства достаточно применить свойство функции 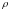, состоящее в том, что из условия 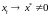следует .

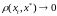Покажем, что для примитивной матрицы функцию в условиях леммы 2.3 можно выбрать не зависящей от выбора .

Лемма 2.4. Пусть – правый вектор Фробениуса устойчивой примитивной матрицы . Тогда для каждого найдется , такое, что для всех ненулевых неотрицательных векторов , таких что , условие выполняется для всех .

Доказательство. Отметим, что в силу примитивности матрицы для всех последовательности относительно функции имеют "одинаковый предел" т.е. .

По лемме 2.3 для и векторов 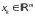найдутся 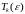, такие что при 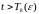справедливо 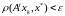. Обозначим .

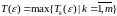Любой вектор представим в ви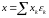де , где 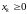. Мы уже показали, что при выполняется 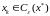, следовательно (по свойству функции ), и 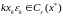. Используя выпуклость нормы, получаем, что .

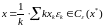Лемма 2.5. Если вектор Фробениуса устойчивой неотрицательной матрицы не содержит нулевых элементов, то найдется число 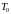, такое что для всех ненулевых неотрицательных векторов для всех 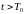выполняется условие .

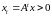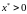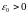Доказательство. Если вектор , то найдется , такое что коническая окрестность состоит только из положительных векторов. Следовательно, по лемме 2.4 для всех выполняется условие 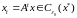, вследствие чего .

Лемма 2.6. Если в задаче 021 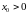и выполняются условия леммы 2.5, то найдется число , такое что для всякой оптимальной траектории 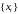этой задачи при 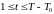выполняется условие .

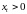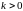Доказательство. Рассмотрим последовательность при некотором . Число 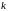можно подобрать так, чтобы последовательность 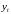была допустимой для задачи 021. Действительно, при подстановке этой последовательности в условие 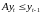при 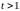получим равенства, а при 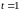имеем 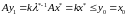. Поскольку , выполнение условия 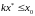можно добиться выбором некоторого . При этом значение целевой функции .

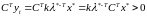Для оптимальной траектории значение целевой функции не может быть меньшим, чем для траект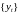ории , поэтому получаем, что в оптимальной траектории .

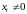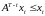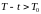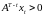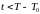Из ограничений задачи и неотрицательности матрицы получаем, что . По лемме 2.5 из неотрицательности вектора получаем, что при вектор , следовательно, при справедливо неравенство .

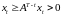Теорема 2.5. Если в задаче 021 вектор Фробениуса матрицы положителен, матрица является примитивной и устойчивой, то вектор является магистралью для задачи 021.

Доказательство. По теореме двойственности в линейном программировании с учетом леммы 2.6 получаем, что для любой оптимальной траектории 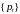двойственной к 021 задачи все ее ограничения с номерами обращаются в равенства

.

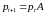Таким образом, при имеет место равенство .

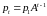По теореме двойственности оптимальные значения целевых функций равны, поэтому 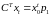, откуда получаем, что .

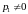Применим к последовательности лемму 2.5. Получаем, что найдется , для которого при 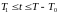справедливо условие .

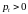Снова применим теорему двойственности, согласно которой при для оптимальной траектории задачи 021 в ограничениях должны выполняться равенства 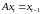. При данных значениях получаем, что .

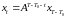Согласно лемме 2.4 получаем, что для каждого найдется , такое, что для при 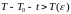выполняется условие .

Таким образом, при 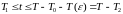для любой оптимальной траектории задачи 021 выполняется условие . Следовательно, вектор является магистралью.