
- •Предмет теории вероятности
- •4.Осн. Правила и формулы комбинаторики
- •6. ГеометрическиОе определение вероятности
- •7. Теоремы сложения вероятностей
- •Свойства функции распределения
- •Свойства математического ожидания
- •20. Нормальное распределение
- •Свойства математического ожидания
- •23. Вероятность попадания нормальной случайной величины в заданный интервал
- •Свойства эмпирической функции распределения
- •33. Точечное оценивание параметров распределения.
- •35. Доверительный интервал и доверительная веротность.
- •36. Доверительные интервалы математического ожидания и для дисперсии нормально распределенной случайной величины.
Свойства функции распределения
Функция распределения принимает значения из промежутка
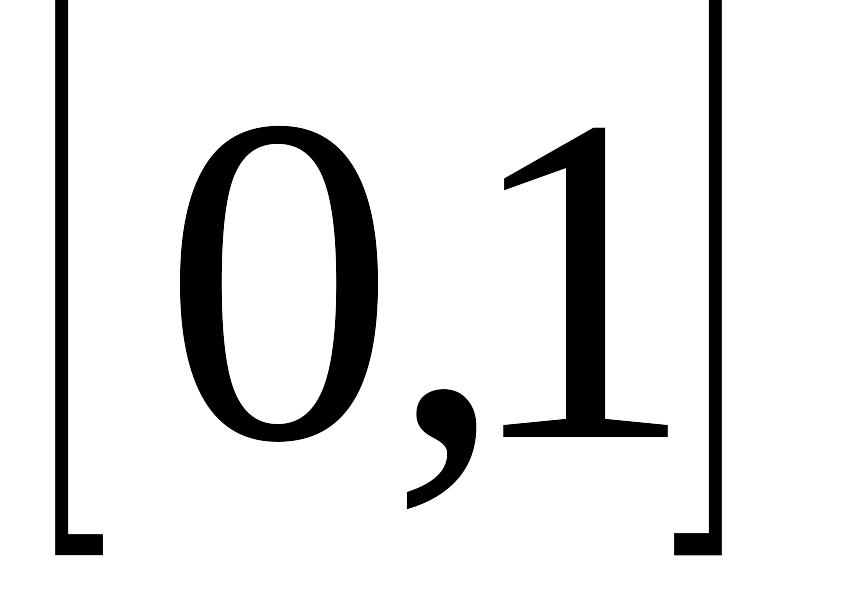 :
:
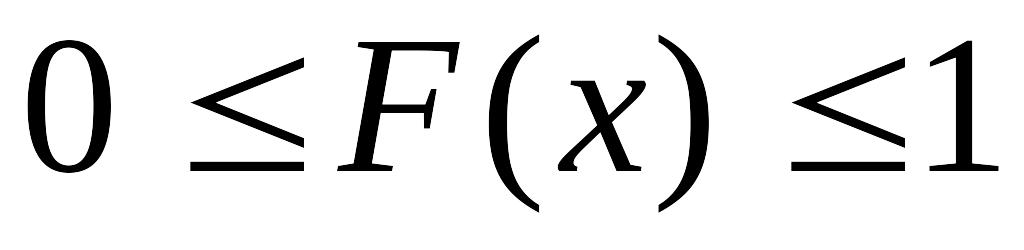 .
.Вероятность того, что случайная величина примет значение из полуинтервала
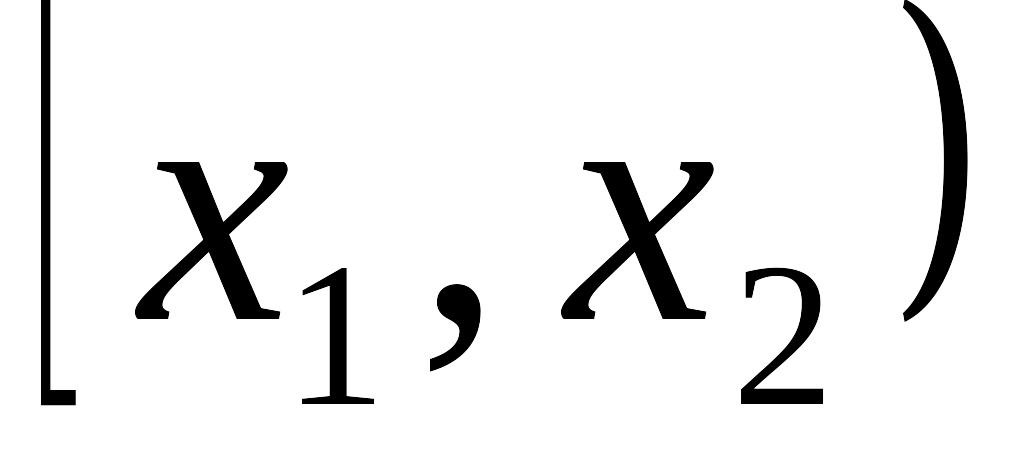 ,
равна разности
,
равна разности
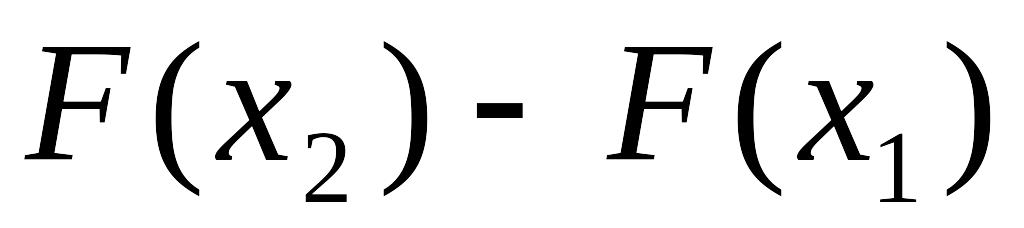 :
:
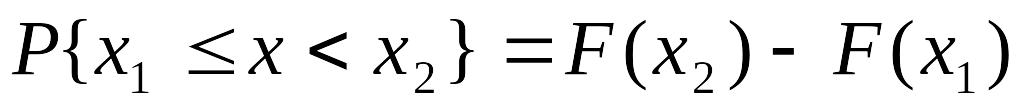 .
.Функция распределения – неубывающая функция, т.е.
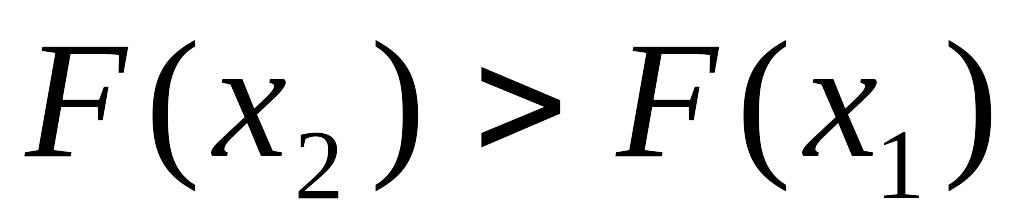 при
при
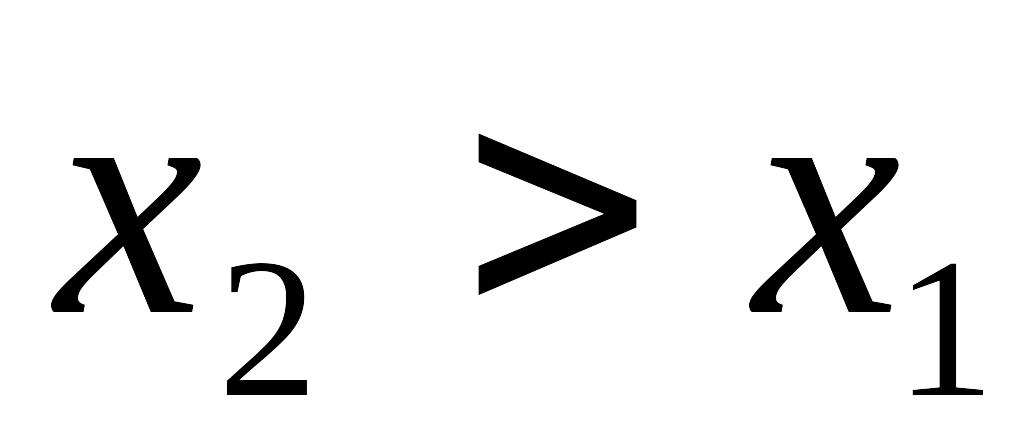 .
.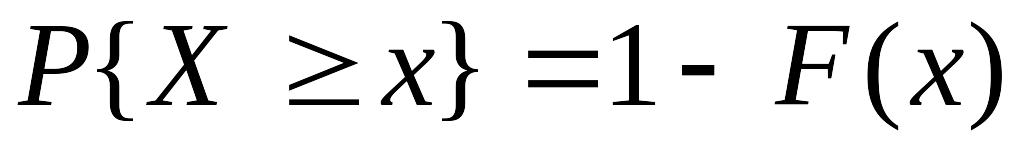 .
.Если
 ,
то
,
то
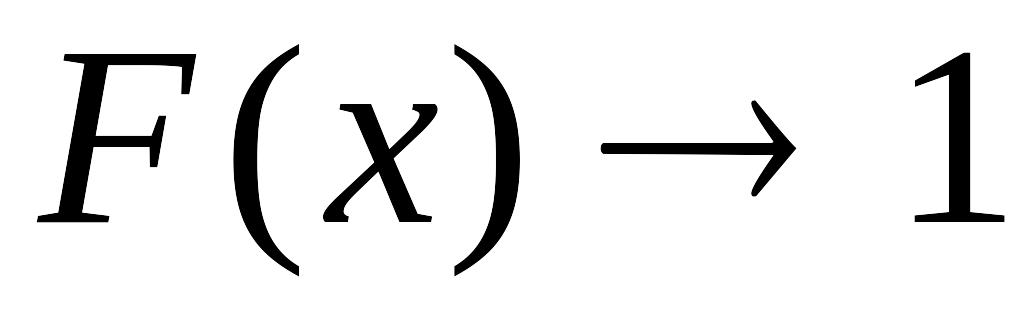 .
.Если
 ,
то
,
то
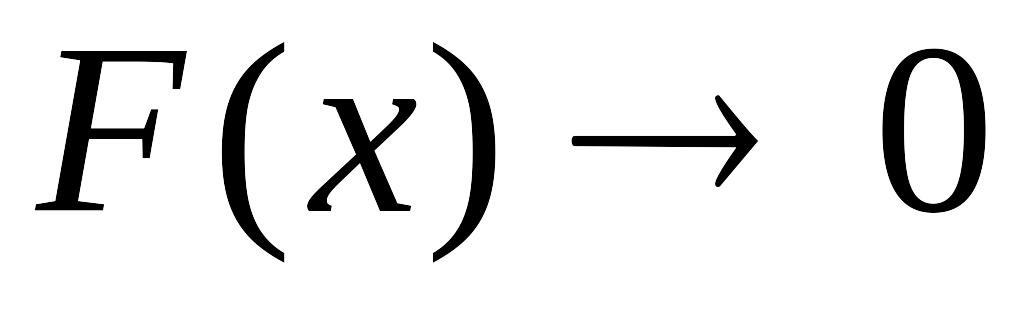 .
.
ОПР: функция распред-я любой дискрет-й случ величины есть разрывчатая ступенчатая функция, скачки которой происходят в точках соотв. возм-х значениям случ величины и равны вероят-м этих значений.
16. Дискретно распределенная случайная величина
ОПР: Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:
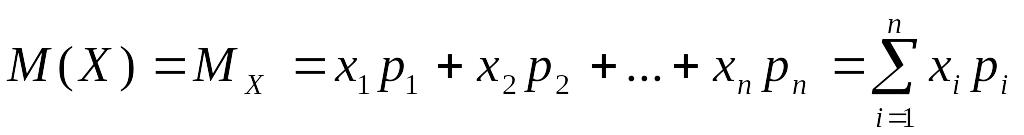 ,
,
где
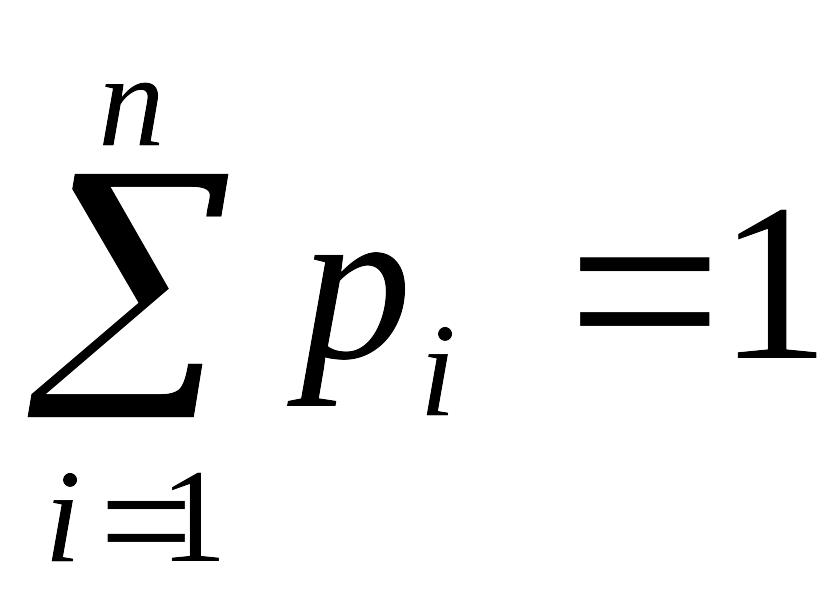 .
.
Свойства математического ожидания
1. Математическое
ожидание постоянной величины
![]() равно этой величине.
равно этой величине.
![]()
2. M(CX)= C·M(X)
3. M(X+Y)=M(X)+M(Y)
4.![]()
5.
![]()
ОПР: Дисперсией
случайной величины
![]() называют математическое ожидание
квадрата отклонения этой величины от
ее математического ожидания:
называют математическое ожидание
квадрата отклонения этой величины от
ее математического ожидания:
![]() .
.
свойства дисперсии
Дисперсия постоянной величины равна нулю.
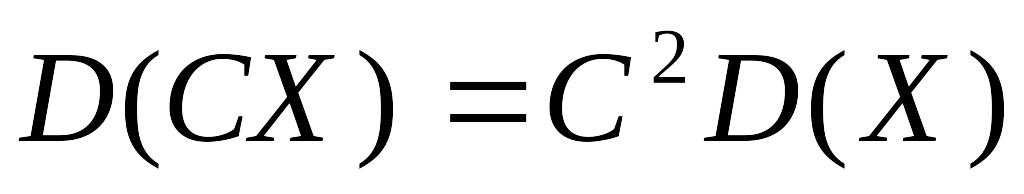
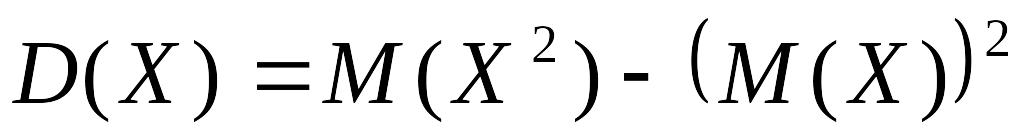
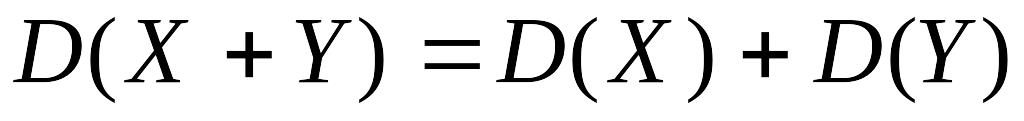
D(X-Y)= D(X)-D(Y)
ОПР: Средним
квадратичным отклонением
![]() (или стандартом)
случайной величины
называется корень квадратный из дисперсии
(или стандартом)
случайной величины
называется корень квадратный из дисперсии
![]() этой величины:
этой величины:
![]() .
.
17. НЕПРЕРЫВНО РАСПРЕДЕЛЕННАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА.
Математическим ожиданием непрерывной случайной величины называется значение интеграла:
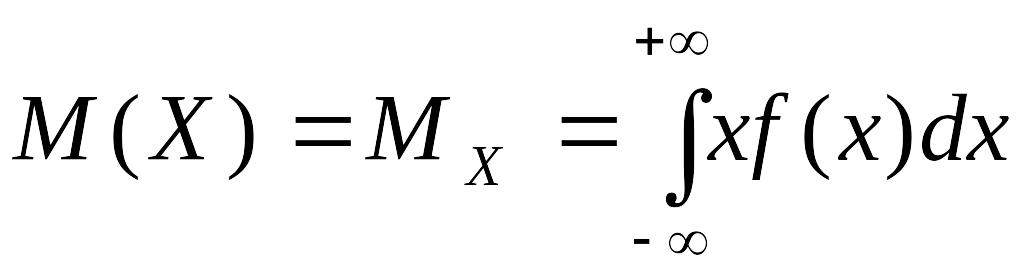
Дисперсией непрерывной случайной величины называется значение интеграла:
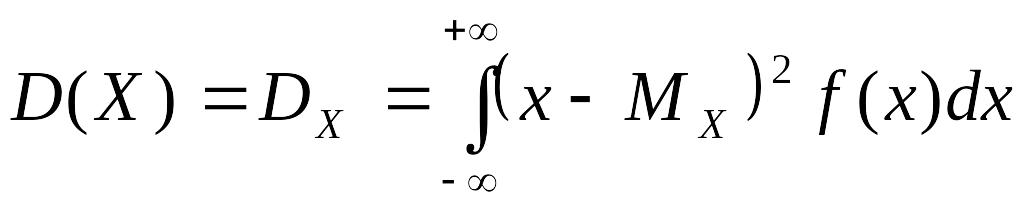 .
.
Среднее квадратичное отклонение непрерывной случайной величины вычисляется как корень квадратный из дисперсии:
![]() .
.
18. БИННОМИНАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
ОПР: законом распределения случайной величины наз соот-ие между значениями случ-й величины и их верот-ми.
Теорема. Математическое ожидание числа появлений события в независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
Теорема.
Дисперсия
числа появлений события
в
независимых испытаниях равна произведению
числа испытаний на вероятности появления
и непоявления события
в одном испытании:
![]() .
.
Биномиальный закон распределения часть приходится применять в условиях, когда число независимых испытаний велико. Вычисление вероятностей по формуле Бернулли при этом усложняется, поэтому представляет интерес асимптотическое приближение для биномиального закона, справедливое при больших . Возможны два случая:
Когда при увеличении числа испытаний математическое ожидание рассматриваемой случайной величины
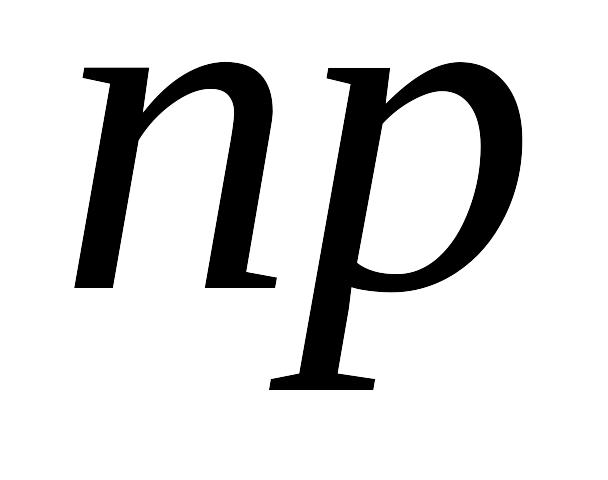 тоже неограниченно возрастает (случай
постоянного
);
при этом биномиальное распределение
сходится к нормальному закону, который
будет рассмотрен позже.
тоже неограниченно возрастает (случай
постоянного
);
при этом биномиальное распределение
сходится к нормальному закону, который
будет рассмотрен позже.Когда при увеличении числа испытаний остается постоянным произведение
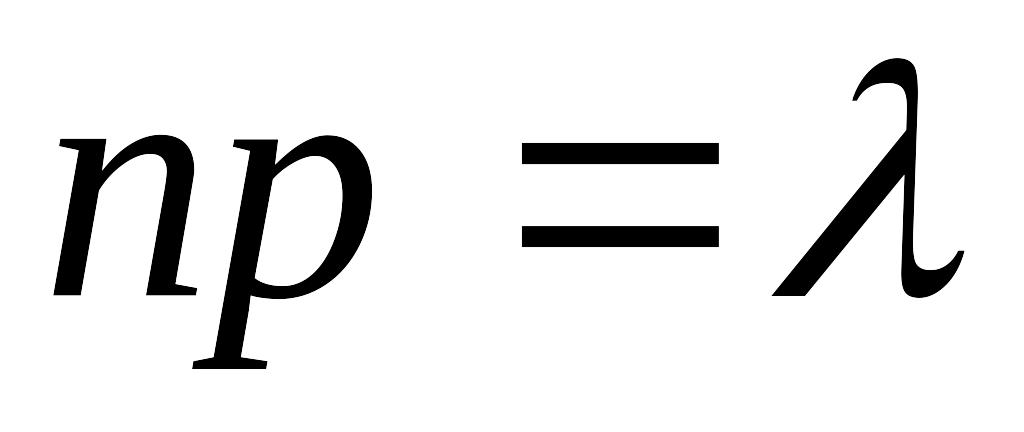 ,
то есть математическое ожидание
рассматриваемой случайной величины
остается конечным. Это означает, что
вероятность события
,
то есть математическое ожидание
рассматриваемой случайной величины
остается конечным. Это означает, что
вероятность события
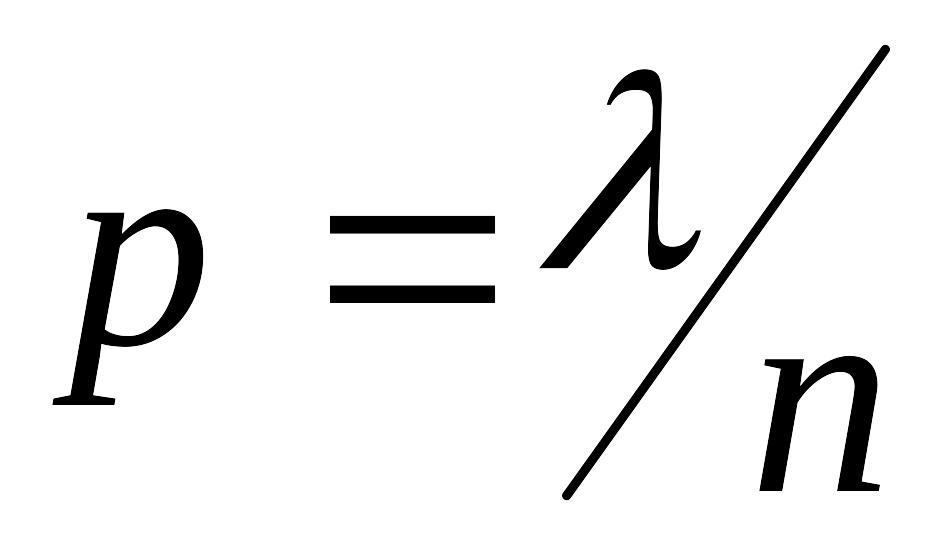 стремится к нулю. В этом случае
биномиальное распределение сходится
к распределению Пуассона.
стремится к нулю. В этом случае
биномиальное распределение сходится
к распределению Пуассона.
19. РАСПРЕДЕЛЕНИЕ ПУАСОНА СЛУЧАЙНОЙ ВЕЛИЧИНЫ
ОПР:Случайная
величина
называется распределенной
по закону Пуассона
с параметром
![]() ,
если эта случайная величина может
принимать значения
,
если эта случайная величина может
принимать значения
![]() ,
соответствующая вероятность которых
определяется по формуле Пуассона, когда
,
соответствующая вероятность которых
определяется по формуле Пуассона, когда
![]() :
:
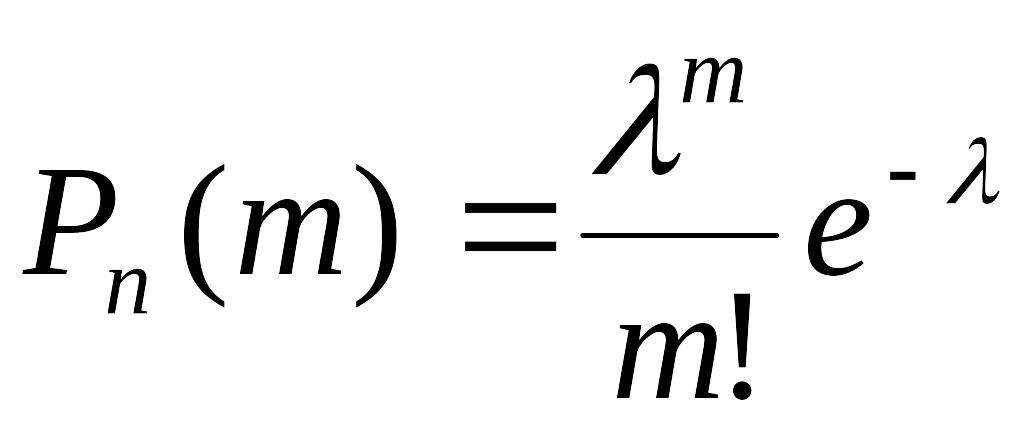
ТЕОРЕМА:
М случ величины распред-ой по закону
Пуассона =λ Д=λ, ϭ(х)=![]()
