3) Поток вектора напряженности. Теорема Гаусса для электростатического поля в вакууме

Вычисление напряженности поля системы электростатических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К. Гауссом теорему, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность.

Поток вектора напряженности через замкнутую поверхность равен интегралу от скалярного произведения:

Поток вектора напряженности электростатического поля системы точечных зарядов в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности, деленной на электрическую постоянную.

Если внутри замкнутой поверхности отсутствуют заряды, то число входящих силовых линий равно числу выходящих, следовательно, число пересечений и сам поток равен нулю.

4) Применение теоремы Гаусса к расчету поля бесконечной плоскости, обладающей равномерно распределенным зарядом, поля двух параллельных бесконечных разноименно заряженных плоскостей

1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость заряжена с постоянной поверхностной плотностью +

( = dQ/dS — заряд, приходящийся на единицу поверхности).

Линии напряженности такого поля перпендикулярны к плоскости и направлены от плоскости в противоположные стороны.

В качестве замкнутой поверхности построим цилиндр, основания которого параллельны этой плоскости, а ось цилиндра перпендикулярная плоскости.

Вся замкнутая поверхность состоит из боковой поверхности цилиндра и площади двух оснований. Поток вектора напряженности будет складываться из боковой поверхности и двух оснований.

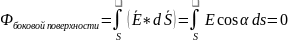
Так как угол между нормали и напряженности 90.

По теореме Гаусса:

Тогда:

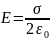(1)

Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.

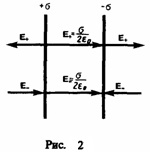
2. Поле двух бесконечных параллельных разноименно зараженных плоскостей

Пусть плоскости заряжены равномерно разными по знаку зарядами с поверхностными плотностями +σ и –σ. Поле таких плоскостей будем искать как суперпозицию полей, которые создаваются каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательно заряженной плоскости. Слева и справа от плоскостей поля вычитаются (поскольку линии напряженности направлены навстречу друг другу), значит здесь напряженность поля E=0. В области между плоскостями E = E₊ + E_- (E₊ и E_- находятся по формуле из выше написанного(1) ), поэтому результирующая напряженность (2) Результирующая напряженность поля в области между плоскостями описывается зависимостью (2), а вне объема, который ограничен плоскостями, равна нулю.