5.2. Уравнение бернулли для элементарной струйки вязкой жидкости при установившемся движении

В этом частном случае удается получить решение уравнений Навье-Стокса. Представим дифференциальные уравнения движения вязкой жидкости в форме Громеки. Для установившегося движения несжимаемой жидкости уравнения имеют вид

(5.5)

где  оператор Лапласа.

Умножим уравнения (5.5) на соответствующие проекции элементарного перемещения dx, dy, dz вдоль струйки и просуммируем:

(5.6)

В этом выражении вычитаемое можно рассматривать как работу сил вязкости на элементарном перемещении вдоль линии тока, отнесенную к единице массы жидкости.

Введя обозначение , получим

,

Т.К. Определитель равен нулю из-за пропорциональности первой и третьей строк (см. Уравнение (4.15)). После интегрирования будем иметь

. (5.7)

Если из массовых сил действует только сила тяжести, получим

. (5.8)

Для двух точек одной и той же линии тока можно записать

.

Имея в виду, что на практике в большинстве случаев удельная ра­бота сил вязкости А₂ > А₁, введем обозначение

.

Тогда окончательно запись уравнения Бернулли для установившегося движения элементарной струйки вязкой несжимаемой жидкости имеет вид

. (5.9)

Для элементарной струйки сжимаемого вязкого газа по аналогии с изложенным (с учетом (4.20)), получим уравнение Бернулли в виде

. (5.10)

Принятые здесь обозначения соответствуют обозначениям п.4.3.

Та часть энергии, которая затрачена на работу сил вязкости, превращается из механической в тепловую. Этот процесс необратим, т.е. обратное превращение невозможно из-за рассеивания тепла в окружающее пространство. Такой процесс называется диссипацией энергии.

5.3. Уравнение бернулли для потока при установившемся движении вязкой жидкости

Полученное в предыдущем параграфе уравнение Бернулли для струйки вязкой несжимаемой жидкости при установившемся движении является основой для вывода уравнения Бернулли для потока. Основной сложностью при решении этого вопроса является определение закона изменения скорости через живое сечение.

В этой связи ниже установим возможность использования для расчетов средней скорости по живому сечению потока.

5.3.1. Удельная энергия потока

Удельная энергия потока (отнесенная к единице веса) складывается из удельной потенциальной и кинетической энергий.

А. Удельная потенциальная энергия потока . В плавно изменяющемся установившемся потоке , а уравнения движения (5.4) имеют вид

(5.11)

где V_i  местная скорость частиц жидкости в i-й точке живого сечения потока.

Два последних уравнения аналогичны уравнениям Эйлера для покоящейся жидкости (2.5). Отсюда можно сделать вывод, что при установившемся плавно изменяющемся движении вязкой жидкости давление по живому сечению распределяется по гидростатическому закону, т.е.

.

Исходя из этого теперь можем определить в уравнении Бернулли для потока удельную потенциальную энергию применительно к любой выбранной в данном живом сечении точке также, как и для элементарной струйки.

Однако надо иметь в виду, что для больших масс движущейся жид­кости (канал, река) это утверждение может и не выполняться. Если поле скоростей потока имеет искривление линии тока, то частицы жидкости движутся по криволинейным траекториям, и гидростатический закон распределения давления в живом сечении нарушается.

Б. Удельная кинетическая энергия потока. Удельная кинетическая энергия массы жидкости, протекающей через живое сечение в единицу времени, вычисленная по местным скоростям потока и отнесенная к единице веса, равна

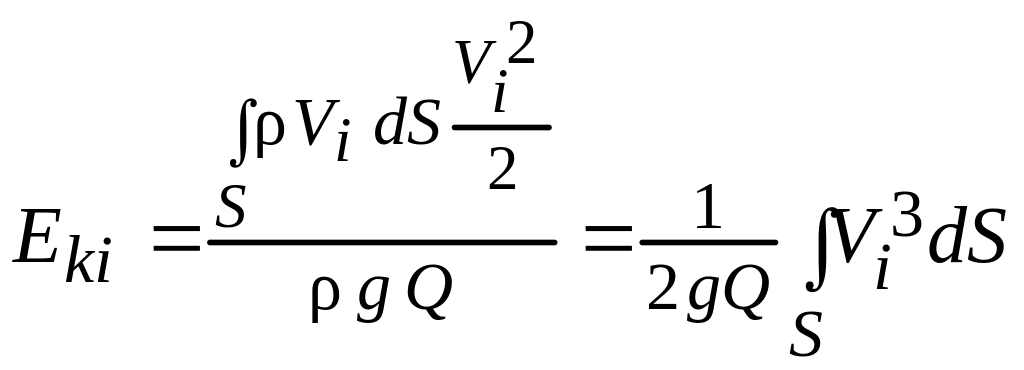, (5.12)

где  кинетическая энергия массы жидкости, протекающей в единицу времени через живое сечение, найденную по элементарным массам (m_i = V_idS), проходящим через площадки dS со скоростью V_j.

Как уже отмечалось выше вычисление E_ki по местным скоростям потока весьма затруднительно, т.к. функция V_i = f (x,y,z) зачастую неиз­вестна. Гораздо проще вычислить удельную кинетическую энергию по средней скорости в живом сечении V_cp = Q/S. В этом случае удельная кинетическая энергия при расходе Q и средней скорости V_cp будет равна

. (5.13)

Возьмем отношение E_ki к E_cp , обозначив его через 

, (5.14)

т.е. есть отношение действительной кинетической энергии массы жид­кости, протекающей через живое сечение потока, к кинетической энер­гии, вычисленной в предположении, что во всех точках живого сечения местные скорости V_i равны средней скорости V_cp.

 называется коэффициентом кинетической энергии или коэффициентом Кориолиса.

При равномерном распределении скоростей по живому сечению потока (рис.5.2, а) коэффициент  равен единице, а при реальном распределении скоростей (рис.5.2, б).  всегда больше единицы.

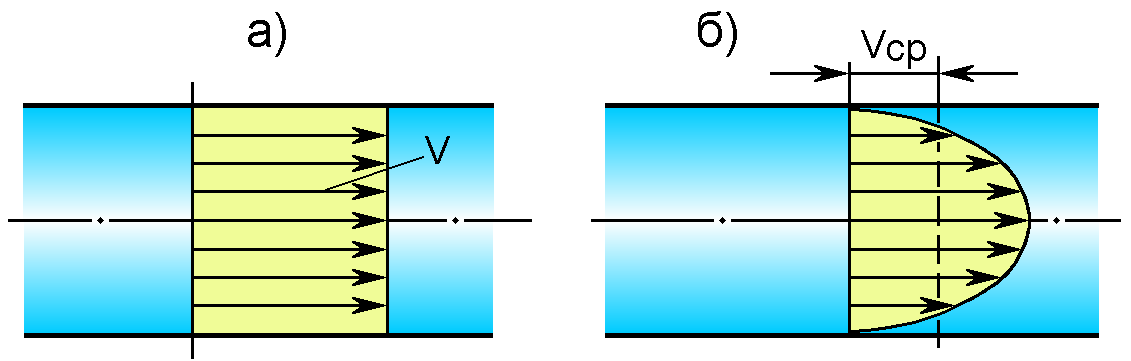
Рис.5.2. Распределение скоростей по живому сечению потока

невязкой (а) и реальной жидкости (б)

Последнее можно доказать, если в формуле (5.14) местную скорость V_i выразить в виде суммы

,

где V - знакопеременная добавка.

Тогда имеем

. (5.14)