Вопрос17. Стандартная форма представления передаточной функции разомкнутой системы.

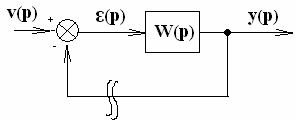
ПФ разомкнутой системы W(p)=y(p)/ε(p) вычисляется в результате алгебраических операций над передаточными функциями звеньев W_i(p)=K_i(p)/D_i(p), , каждая из которых представляет собой отношение многочленов от р.

Следовательно, ПФ разомкнутой системы также можно представить в виде отношения двух многочленов W(p)=K(p)/D(p).

В теории управления принято записывать эту ПФ в стандартной форме, т.е. как

,

где - нормированная ПФ разомкнутой системы, удовлетворяющая условию W₀(0)=1; ν – число интегрирующих звеньев, входящих в ПФ, от числа интегрирующих звеньев зависит точность системы; k – коэффициент усиления разомкнутой системы (контура), определяемый выражением

.

Выясним физический смысл коэффициента усиления. Для этого, используя выражение

найдем уравнение разомкнутой системы в изображениях.

.

Здесь представляет собой преобразование Лапласа от ν-той производной управляемой величины предварительно невозбужденной системы.

Пусть ошибка является постоянным сигналом ε(t)=ε₀=const, так что ее изображение ε(р)= ε₀/р. При этом установившееся значение ν-ой производной находим по теореме о конечном значении:

= .

Отсюда, коэффициент усиления разомкнутой системы представляет собой отношение установившегося значения ν-ой производной ее реакции и постоянного входного сигнала:

Размерность k=[c^-ν]

Пример. Преобразуем ПФ к стандартному виду. Т.к. ν=1, то k=20с^-1 и

.

18 Корневые методы оценки качества переходного процесса

Переходную характеристику h(t), представляющую собой переходный процесс при единичном ступенчатом воздействии, можно рассматривать как сумму установившейся h_ycm и переходной h_nep(t) составляющих. Выражение для переходной составляющей зависит от нулей z_j и полюсов p_i замкнутой системы и определяется соотношением

(87)где .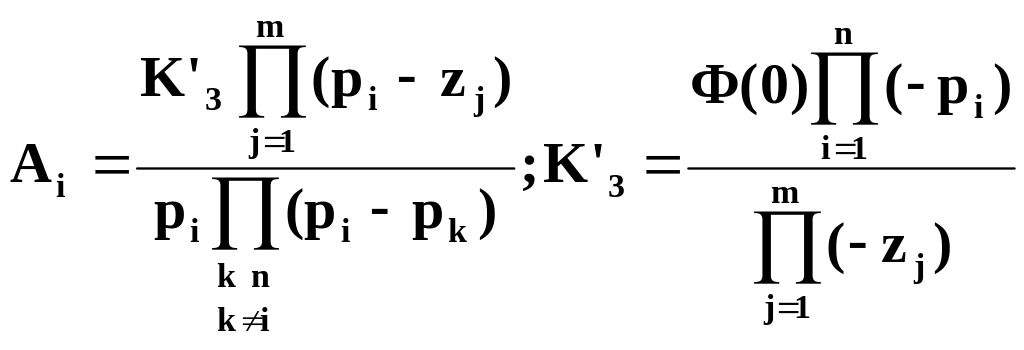

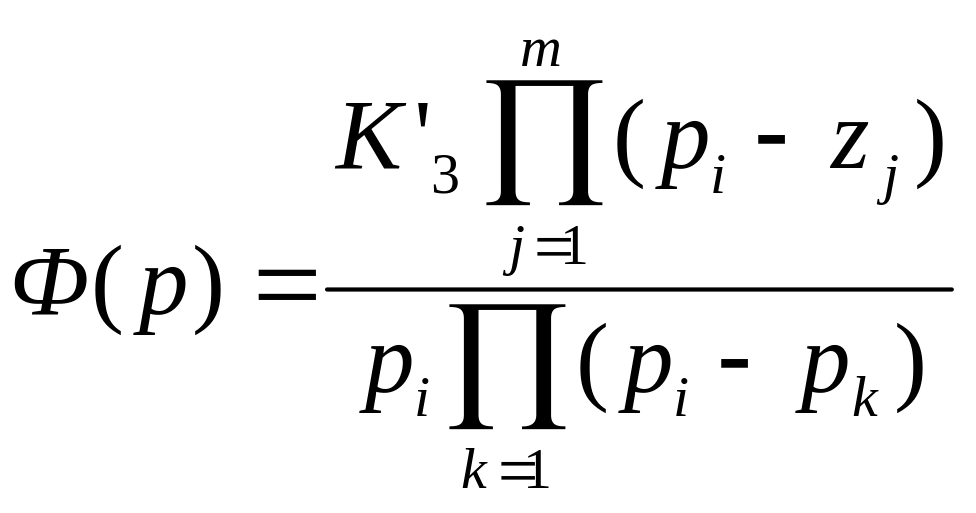При выводе выражения (87) использовалось представление передаточной функции замкнутой системы в виде

По расположению ее нулей и полюсов можно судить о качестве системы.

Оценка перерегулирования.

Перерегулирование системы зависит от поведения колебательных составляющих

,

так как колебательные процессы в системе будут наблюдаться только в том случае, когда характеристическое уравнение содержит комплексно-сопряженные корни . Склонность системы к колебаниям характеризует оценка , которую называют колебательностью.

Таким образом, чем больше величина , тем более колебательный характер будут иметь переходные процессы и наоборот. В пределе при =∞ полюса системы будут «чисто» мнимыми, и в ней будут наблюдаться переходные процессы в виде незатухающих колебаний. В случае, когда =0, все корни характеристического уравнения будут вещественными и в системе будут возникать апериодические процессы. Эмпирическим путем установлена взаимосвязь между колебательностью и перерегулированием в виде соотношения

.

Отметим, что при значение перерегулирования в системе составит .

Связь колебательности и относительного коэффициента затухания определяется формулой

.

Рассмотренные корневые методы оценки не учитывают влияние на постоянные коэффициенты А_i других нулей и полюсов замкнутой системы, наличие которых, как это видно из выражения (87), может существенно изменить качество переходного процесса.

Анализируя выражение (87), можно сделать следующие выводы относительно влияния расположения нулей и полюсов на вид и характер переходной характеристики.

1) Основное влияние на качество переходного процесса оказывает группа ближайших к мнимой оси нулей и полюсов (так называемых доминирующих нулей и полюсов).

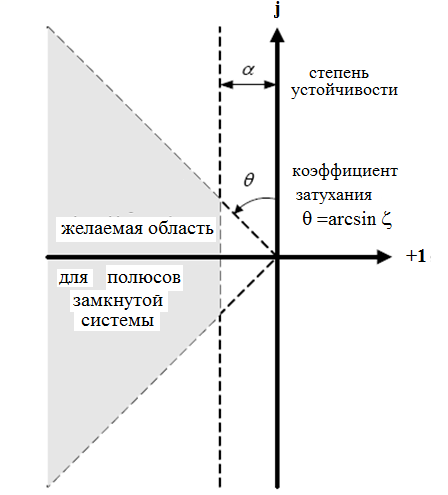
2) Длительность переходного процесса в основном определяется степенью устойчивости системы, равной абсолютному значению вещественной части ближайших к мнимой оси комплексных полюсов замкнутой системы или вещественного полюса, если он является ближайшим к мнимой оси. При этом длительность переходного процесса может быть определена по формуле

3) Величина перерегулирования зависит от степени колебательности доминирующих комплексных полюсов и от степени близости к мнимой оси остальных нулей и полюсов замкнутой системы.

4) Близкие к мнимой оси нули увеличивают перерегулирование, а близкие (но не доминирующие) полюсы его уменьшают.

Не останавливаясь на доказательстве всех этих пунктов, приведем лишь соображения, подтверждающие вывод об увеличении перерегулирования при введении в систему нулей.

Пусть САУ описывается в отсутствии нулей передаточной функцией Ф₀(р). Введем в эту систему нуль z=- , так чтобы при этом не изменился коэффициент усиления замкнутой системы k_з=Ф₀(р). Тогда передаточная функция примет вид

По изображению

найдем переходную характеристику полученной системы

,

как сумму переходной характеристики исходной и взвешенной производной этой характеристики.

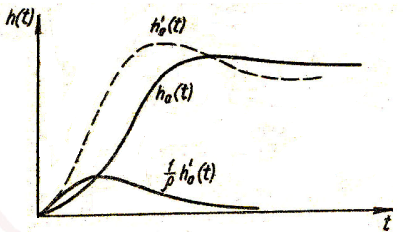В начале переходного процесса характеристика h(t) возрастает с большой скоростью и поэтому ее производная h’₀(t) положительна и имеет большую величину. В результате сложения кривых h₀(t) и получается кривая h(t), имеющая увеличенное перерегулирование, причем перерегулирование увеличивается тем значительнее, чем меньше абсолютное значение нуля передаточной функции Ф(р).

Введение большего числа нулей приводит к тому же эффекту.

Рис. 24

Для системы второго порядка с комплексно-сопряженными полюсами введение нуля увеличивает перерегулирование при а<4.

19.Определение устойчивости линейных САУ по виду корней характеристического уравнения. Геометрическая интерпретация условий устойчивости. Теоремы А.М. Ляпунова.

Определение устойчивости линейной системы по виду корней характеристического уравнения

Поведение линейных систем описывается линейным дифференциальным уравнением. Поэтому исследование устойчивости таких систем сводится к исследованию линейного ДУ. Используя выражение для ПФ замкнутой системы 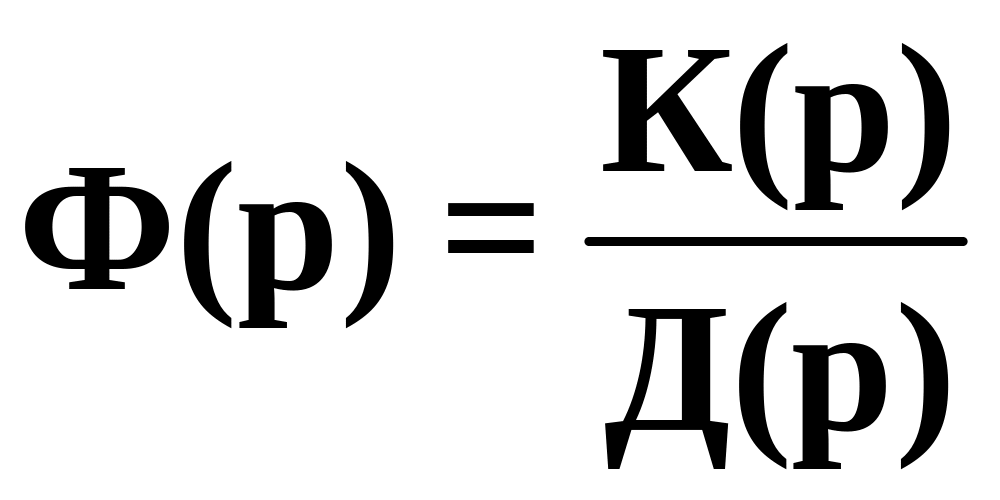,уравнение движения системы в изображениях представим в виде Д(р)y(р)=К(р)v(р) (1). Так как анализ устойчивости производится после прекращения внешнего воздействия, т.е. при v=0, то ДУ свободного движения системы в изображениях будет иметь вид

Д(р)y(р)=0(2)или .

Данное уравнение, записанное в обычной форме (3)

представляет собой однородное уравнение с постоянными коэффициентами, а его общее решение y_cв(t) характеризует свободное движение системы, т.е. движение системы в отсутствие внешнего воздействия. Внешнее воздействие, которое действует на систему до начального момента t=0, влияет на ненулевые начальные условия (или их) порождает и от них (начальных условий) зависит свободное движение.

Если с течением времени свободное движение затухает, т.е. если ,то система будет устойчивая. Если с течением времени свободное движение неограниченно возрастает, т.е. если

,то такая система будет неустойчивая.

Наконец, в промежуточном случае, когда с течением времени y_cв(t) не возрастает неограниченно и не стремится к нулю, говорят, что система является находится на границе устойчивости. Таким образом, устойчивость системы зависит от характера изменения y_cв(t) с ростом времени.

Решение однородного ДУ (3) можно представить (за исключением случая кратных корней) в виде

,(4) где р₁, р₂,…, р_n – корни характеристического уравнения замкнутой системы Д(р)=0, а А₁, А₂,…,А_n – произвольные постоянные, зависящие от значения y_cв(t) и ее производных в начальный момент времени. Величина y_cв(t) будет с течением времени стремиться к нулю только в том случае, если каждое слагаемое выражения (4) также будет стремиться к нулю.

1) Линейная замкнутая система автоматического управления устойчивая, если все корни ее характеристического уравнения Д(р)=0 отрицательны или имеют отрицательную вещественную часть (рис. 2а, в), т.е. .

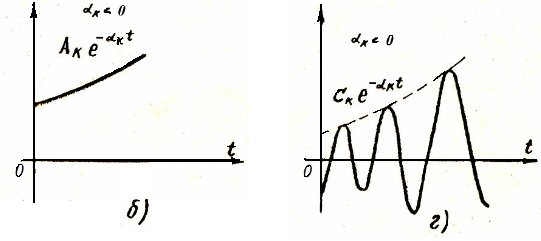
2) Линейная замкнутая система автоматического управления неустойчивая, если хотя бы один из корней ее характеристического уравнения Д(р)=0 имеет положительную вещественную часть или имеются кратные корни с нулевой вещественной частью (рис. 2б, г).

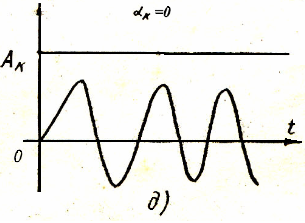
3) Линейная замкнутая система автоматического управления предельно (критически, маргинально) устойчивая, если вещественная часть комплексно-сопряженных корней ее характеристического уравнения Д(р)=0 равна нулю или один вещественный корень равен нулю, а все остальные корни имеют отрицательные вещественные части и нет кратных корней с нулевой вещественной частью (рис. 2д).

Геометрическая интерпретация условий устойчивости.

Корни характеристического уравнения удобно изображать в виде точек на комплексной плоскости, по осям которой откладываются действительные и мнимые части этих корней (рис. 3). Такая плоскость называется плоскостью корней. Если вещественная часть какого-либо корня отрицательная, то точка, изображающая этот корень, будет лежать слева от мнимой оси. Следовательно, для того, чтобы линейнаясистема автоматического управления была устойчивой, необходимо и достаточно, чтобы все корни ее характеристического уравнения Д(р)=0 располагались в плоскости корней

слева от мнимой оси, т.е. были левыми.

П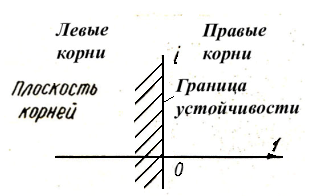 ри изменении параметров системы корни, перемещаясь в комплексной плоскости, могут перейти из левой половины плоскости в правую, т.е. стать правыми, что будет свидетельствовать о превращении устойчивой системы в неустойчивую. Следовательно, линейная система будет неустойчивой, если хотя бы один корень ее характеристического уравнения является правым или, по крайней мере, один кратный нулевой корень или кратные комплексно-сопряженные корни расположены на мнимой оси.

Таким образом, мнимая ось является как бы границей, разделяющей плоскость корней на две области, одна из которых соответствует устойчивости системы, другая – неустойчивости.

Говорят, что линейная система находится на границе устойчивости или критически устойчивая, если пара комплексно-сопряженных корней (колебательная граница устойчивости) или один действительный корень (апериодическая граница устойчивости) лежат на мнимой оси, а все остальные корни располагаются слева от этой оси и нет кратных корней, расположенных на мнимой оси.

На рисунке ниже показано, каким образом можно оценить устойчивость линейной замкнутой системы по расположению корней ее характеристического уравнения на комплексной плокостиp_k (плоскости корней характеристического уравнения).

З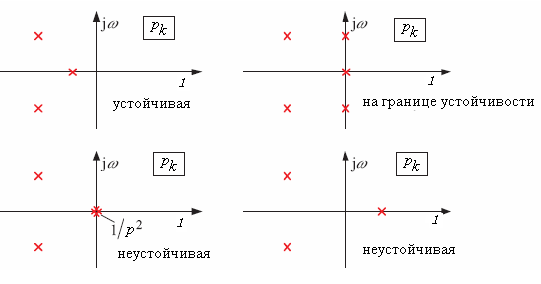 аметим, что корни характеристического уравнения имеют другое название, а именно полюсы системы или полюсы передаточной функции системы. Поэтому все вышеприведенные выводы, касающиеся устойчивости системы, остаются в силе, если мы заменим в них слова «корни характеристического уравнения» на слова «полюсы системы».

Теоремы Ляпунова об устойчивости по линейному приближению.

Теорема 1. Если все корни характеристического уравнения линеаризованной системы имеют отрицательные вещественные части, то исходная система, описываемая нелинейными уравнениями, будет устойчивой.

Теорема 2. Если среди корней характеристического уравнения линеаризованной системы имеется хотя бы один корень с положительной вещественной частью, то исходная нелинейная система будет неустойчивой.

Теорема 3. При наличии нулевых и чисто мнимых корней поведение исходной нелинейной системы не может быть определено по линеаризованным уравнениям и, необходимо проводить дополнительное исследование для решения вопроса об ее устойчивости.