75. Понятия дифференциального уравнения и его решения. Порядок дифференциального уравнения. Общее, особое, частное решения.

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Простейшим дифференциальным уравнением является уравнение вида

Чтобы его решить, нужно представить производную как домножить обе части уравнения на dx и проинтегрировать обе части получившегося уравнения:

Как видно, это уравнение имеет бесконечное количество решений, отличающихся друг от друга на постоянную C . Выбрать конкретное решение уравнения можно, если знать начальные условия, например, точку, через которую проходит график функции y  =  y  ( x ). Так, если известно, что y  ( x ₀ ) =  y ₀, то подставляя это значение в общее решение получаем  откуда и . Это решение можно записать в виде .

Общим решением дифференциального уравнения называется функция y  =  y  ( x ,  C ₁,  C ₂,…,  C _n ), зависящая от n констант, если она является решением дифференциального уравнения при любых значениях постоянных C ₁, C ₂,…, C _n .

Частным решением дифференциального уравнения называется решение, получаемое из общего решения путем придания определенного значения постоянным C _i .

Наряду с частными существуют особые решения , которые нельзя получить из общего решения никакой подстановкой постоянных.

76. Задача Коши для уравнения первого порядка. Теорема существования и единственности. (Формулировка).

Рассмотрим систему обыкновенных дифференциальных уравнений n–го порядка

или

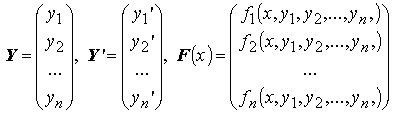
Задачей Коши для для этой системы называется следующая задача: найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x₀)=Y₀, где Y₀ — некоторый постоянный вектор.

Справедлива следующая теорема о существовании и единственности решения задачи Коши.

Теорема Коши. Пусть в области D из Rⁿ⁺¹ непрерывны все компоненты вектора правой части F(x,Y) и их частные производные по Y:

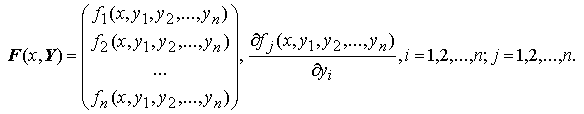
Тогда, какова бы ни была начальная точка (x₀,Y₀) ≡ (x₀,y_{1, 0} ,y_{2, 0}, … ,y_{n, 0} ) ∈ D , существует такой отрезок [x₀ − h; x₀ + h] , что задача Коши   Y' = F(x,Y), что Y(x₀)=Y₀ имеет единственное решение.

Важно понимать, что теорема Коши имеет локальный характер: существование решения Y = Y(x) гарантируется лишь в достаточно малой окрестности точки x₀ , ( h > 0 может оказаться достаточно малым).

Важно также понимать, что теорема содержит только достаточные условия существования и единственности решения — при нарушении условий теоремы задача Коши может иметь или не иметь решений, может иметь несколько решений.

77. Поле направлений. Изоклины. Семейство интегральных кривых уравнения первого порядка.

Для дифференциального уравнения y' = f (x, y), правая часть которого f(x, y), и ее частная производная f_y(x, y) непрерывны в некоторой области D,имеет место геометрическая интерпретация, называемая полем направлений. Если через каждую точку (x, y) области D провести некоторый отрезок l(x, y) с угловым коэффициентом f(x, y), то получится геометрическая картина, называемая полем направлений: любая интегральная кривая y = y(x) уравнения y' = f(x, y) в каждой своей точке (x, y(x)) касается отрезка l(x, y).

Изокли́на дифференциального уравнения первого порядка — линия, на всём протяжении которой наклон, определяемый уравнением, сохраняет постоянное значение.

Изоклина дифференциального уравнения y' = f(x, y), отвечающая наклону p, определяется уравнением f(x, y) = p. Придавая параметру p различные значения, получим сеть изоклин, с помощью которых строятся приближённые линии данного уравнения в виде ломанных с вершинами на изоклинах сети и наклонах звеньев, определяемых параметром. Все точки локальных экстремумов линий данного уравнения лежат на нулевой изоклине. С помощью изоклин определяются и другие геометрические характеристики линий уравнения.

График любого частного решения дифференциального уравнения называется интегральной кривой. Общему решению соответствует семейство интегральных кривых. Задание начального условия 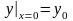означает задание точки 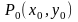, через которую должна проходить интегральная кривая, соответствующая искомому частному решению. Таким образом, отыскивание частного решению. Таким образом, отыскивание частного решения по начальному условию геометрически означает, что из семейства интегральных кривых мы выбираем ту, которая проходит через точку . Согласно теореме существования и единственности решения через каждую точку, в которой функции 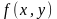и непрерывны, проходит одна единственная интегральная кривая. Если в данной точке эти условия нарушены, то это означает, что через эту точу либо вообще не проходит ни одна интегральная кривая, либо проходит несколько.