88. Системы линейных дифференциальных уравнений с постоянными коэффициентами. Задача Коши. Теорема существования и единственности решения.
Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.
Нормальной системой линейных ДУ с действительными коэффициентами, называется система вида:
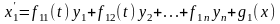
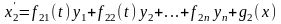
………………………………………. (1)
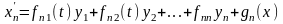
или более коротко
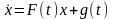(2)
где
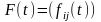- действительная матрица, а
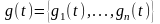- действительный вектор, определенный
при
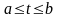
Однородной системой линейных уравнений, соответствующей системе (2), называется система уравнений
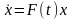(3)
Система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид
,
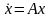(1.1)
где
-
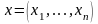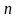-мерный
вектор,
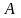- постоянная квадратная матрица размера
.
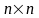89. Подстановка и матричный методы построения общего решения однородной системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.
Общим решением линейной системы уравнений (2) называется множество всех решений этой системы.
Теорема.
Пусть
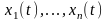- фундаментальная система решений
однородной системы уравнений (3), тогда
формула
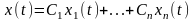(15)
где
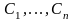- произвольные постоянные, дает общее
решение этой системы. Множество всех
решений однородной системы уравнений
(3) образует
-мерное
векторное пространство, базисом которого
может служить любая фундаментальная
система решений.
Построение фундаментальной системы решения однородной системы с постоянными коэффициентами методом Эйлера
Система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид
, (1.1)
где - -мерный вектор, - постоянная квадратная матрица размера .
Метод Эйлера заключается в следующем. Решение системы (1.1) ищем в виде
,
.
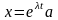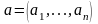(2.1)
Функция
(2.1) является решением системы (1.1), если
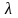- собственное значение матрицы
,
а
- собственный вектор этой матрицы,
соответствующий числу
.
Если собственные значения
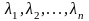матрицы
попарно различны и
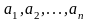- соответствующие собственные векторы
этой матрицы, то общее решение системы
уравнений (1.1) определяется формулой
,
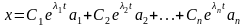где
- произвольные числа. Если для кратного
собственного значения
матрицы
имеется столько линейно независимых
собственных векторов
,
какова его кратность, то ему соответствуют
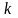линейно независимых решений исходной
системы:
.
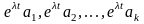Если
для собственного значения
кратности
имеется только
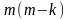линейно независимых собственных
векторов, то решения, соответствующие
,
можно искать в виде произведения
векторного многочлена степени
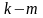на
,
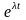т. е. в виде
.
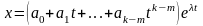Чтобы
найти векторы
,
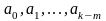надо подставить выражение (2.1) в систему
(1). Приравняв коэффициенты в левой и
правой частях системы, получим уравнения
для нахождения векторов
.
Если
среди собственных чисел матрицы
имеются комплексные числа, то указанным
выше методом строится соответствующее
такому собственному числу решение
системы (1.1) через комплексные функции.
Чтобы выразить решение через действительные
функции (в случае действительной матрицы
),
надо воспользоваться тем, что вещественная
и мнимая части комплексного решения,
соответствующего собственному числу
(
),
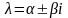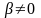являются линейно независимыми решениями.