Свойства

• Всякая последовательность является своей подпоследовательностью.

• Для всякой подпоследовательности 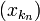верно, что .

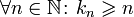• Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.

• Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.

• Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.

• Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.

• Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.

• Частичный предел некоторой последовательности — это предел одной из её подпоследовательностей, если только он существует. Для сходящихся числовых последовательностей частичный предел совпадает с обычным пределом в силу единственности последнего, однако в самом общем случае у произвольной последовательности может быть от нуля до бесконечного числа различных частичных пределов. При этом, если обычный предел характеризует точку, к которой элементы последовательности приближаются с ростом номера, то частичные пределы характеризуют точки, вблизи которых лежит бесконечно много элементов последовательности.

• Два важных частных случая частичного предела — верхний и нижний пределы.

• Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов. В некоторой литературе в случаях, если из последовательности удаётся выделить бесконечно большую подпоследовательность, все элементы которой одновременно положительны или отрицательны, её частичным пределом называют соответственно 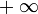или .

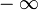• Нижний предел последовательности — это наименьший элемент множества частичных пределов последовательности.

• Верхний предел последовательности — это наибольший элемент множества частичных пределов последовательности.

• Иногда нижним пределом последовательности называют наименьшую из её предельных точек, а верхним — наибольшую. Очевидно, что эти определения эквивалентны.

• Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.  Доказательство. Пусть последовательность ограничена, то есть существует такой отрезок [а, b], что х_n [а, b] n = 1, 2, 3, … Разделим отрезок [а, b] пополам, и по крайней мере один из получившихся отрезков содержит бесконечно много элементов данной последовательности. Пусть это будет отрезок [а₁, b₁], и так далее. Получим систему вложенных отрезков [a, b] 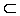[a₁,b₁] [a₂,b₂] … [a_n,b_n] … Выберем по одному элементу последовательности из каждого отрезка

• Последовательность {x_nk} является подпоследовательностью последовательности {x_n}. Так как

• то существует такая точка ξ [а, b], что

• Так как a_n ≤ x_n ≤ b_n, то

14. ВЕРХНИЙ И НИЖНИЙ ПРЕДЕЛЫ

- 1) В. и н. п. последовательности - наибольший, и соответственно, наименьший, предел среди всех частичных пределов (конечных и бесконечных) данной последовательности действительных чисел. Для любой последовательности действительных чисел множество всех ее частичных пределов (конечных и бесконечных) на расширенной числовой прямой (т. е. в множестве действительных чисел, пополненном символами ) не пусто и имеет как наибольший, так и наименьший элементы (конечный пли бесконечный). Наибольший элемент множества частичных пределов наз. верхним пределом (в. п.) последовательности и обозначается

наименьший элемент - нижним пределом (н. п.) н обозначается

Напр., если

то

если

то

если

то

У всякой последовательности существует в. п. (н. п.), при этом, если последовательность ограничена cверху (снизу), то ее в. п. (н. п.) конечен. Для того чтобы число а было в. п. (соответственно н. п.) последовательности необходимо н достаточно, чтобы для любого выполнялись условия: а) существует такой номер , что для всех номеров справедливо неравенство ; б) для любого номера пД существует такой номер , что Условие а) означает существование при любом фиксированном в последовательности лишь конечного числа таких членов , что . Условие б) означает существование бесконечного множества таких членов , что . Понятие н. п. сводится к понятию в. п. с помощью изменения знака у членов последовательности:

Для того чтобы последовательность имела предел (конечный или бесконечный, равный одному из символов ), необходимо и достаточно, чтобы

КОМПАКТНОСТИ ПРИНЦИП

в теории функций комплексного переменного - условие компактности семейств аналитических функций. Бесконечное семейство Ф={f(z)} голоморфных функций в области Dкомплексной плоскости, z называется компактным, если из любой последовательности можно выделить подпоследовательность, сходящуюся к аналитической функции в Dили, что то же самое, равномерно сходящуюся внутри D, т. е. равномерно сходящуюся на любом компакте для того чтобы семейство Ф было компактным, необходимо и достаточно, чтобы оно было равномерно ограниченным внутри D, т. е. равномерно ограниченным на любом компакте

Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши — последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии не более чем заданное.

Последовательность точек метрического пространства (X,ρ) называется фундаментальной, если она удовлетворяет критерию Коши:

для любого существует такое натуральное N_ε, что для всех n,m > N_ε.

Теорема ( Критерий Коши ). Для того, чтобы последовательность {x_n} сходилась, необходимо и достаточно чтобы она была фундаментальной.

Доказательство:

Необходимость. Пусть {xn} сходится.

Достаточность. Пусть {x_n} - фундаментальная последовательность. Докажем, что она ограничена и .

Так как последовательность фундаментальна, то , в -окресности которой существуют все элементы x₁,x₂,x₃,...,x_{N − 1}.

Предположим, A = max{ | x₁ | , | x₂ | , | x₃ | ,..., | x_{N − 1} | , | x_n − ε | , | x_n + ε | }.

В отрезке [A, -A] содержатся все элементы последовательности, т.е. {x_n} - ограниченна.

В следствие теоремы Больцано-Вейерштрасса ( ) < (x_n − ε;x_n + ε).

в силу произвольности

15. Определение предела функции в точке по Коши.

Определение предела функции в точке a по Коши. Пусть f(x) определена на множестве X, и a - предельная точка X. Число b называется пределом f(x) при x  a, если для   > 0   > 0 такое, что для  x  {0 < x - a< }: f(x) - b < .

Предел (по Гейне) функции в точке: пусть  - предельная точка области определения функции. Тогда , если для любой последовательности значений аргумента, удовлетворяющей следующим условиям:  

.

.

выполняется .

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Пусть на некотором числовом множестве задана числовая функция и число — предельная точка области определения . Существуют различные определения для односторонних пределов функции в точке , но все они эквивалентны.

Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < . Запись этого факта:

Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа  < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < . Записывается это так:

16. Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.