3.2. Постановка игровых задач.

Формальное описание задачи принятия решения можно представить в виде математической модели, задав множество , элементы которого в теории игр называют альтернативами, множество , элементы которого называются исходами и множество , элементы которого называются показателями среды, характеризующие условия коммерческой деятельности.

При анализе ситуаций, возникающих в коммерческой практике, множество X описывает набор принимаемых решений одной стороны, множество Y — возможные варианты поведения противоположной стороны, а множество A — тот выигрыш (или проигрыш), который получит игрок.

Если каждая альтернатива может привести к одному из исходов, каждый из которых имеет определенную вероятность появления, то считается, что принятие решения происходит в условиях риска.

Если каждая альтернатива может привести к одному из нескольких исходов, причем отсутствует даже стохастическая зависимость исходов от альтернатив, то считается, что принятие решения происходит в условиях неопределенности.

Каждый исход a  A является функцией двух аргументов: , где x  X, y  Y. Функция F называется функцией реализации и она сопоставляется исход по каждой паре - «альтернатива - состояние среды».

Функцию реализации удобно представить в виде так называемой платежной таблицы.

y₁ ... y_j ... y_m

x₁ F(x₁, y₁) ... F(x₁, y_j) ... F(x₁, y_m)

... ... ... ... ... ...

x_i F(x_i, y₁) ... F(x_i, y_j) ... F(x_i, y_m)

... ... ... ... ... ...

x_n F(x_n, y₁) ... F(x_n, y_j) ... F(x_n, y_m)

3.3. Методы и модели решения игровых задач. Принцип минимакса.

Рассмотрим методы и модели решения игровых задач.

Рассмотрим конечную парную игру с нулевой суммой. Игрок I имеет m стратегий (А₁, А₂, ..., А_m), а игрок II — n стратегий (В₁, В₂, ..., В_n). Такая игра называется игрой размерностью m  n. Пусть каждая сторона определилась с выбором стратегии: игрок I — A_i (i = 1, 2, ..., m), игрок II — B_j (j = 1, 2, ..., n). Выигрыши игрока I — (A_i, B_j) и игрока II — (A_i, B_j) удовлетворяют соотношению (A_i, B_j) + (A_i, B_j) = 0.

Если игра состоит только из личных ходов, то выбор стратегии (A_i, B_j) однозначно определяет исход игры , т.е. выигрыш игрока I. Если игра содержит также случайные ходы, то выигрыш при паре стратегий (A_i, B_j) есть величина случайная, зависящая от исходов всех случайных ходов. В этом случае ожидаемый выигрыш — это среднее значение (математическое ожидание). Предположим, что значения a_ij известны для каждой пары стратегий (A_i, B_j). Построим таблицу, строки которой соответствуют стратегиям игрока I, а столбцы — стратегиям игрока II, т.е. платежную матрицу. Каждый элемент (a_ij > 0) матрицы определяет величину выигрыша игрока I и проигрыш игрока II. Цель игрока I — максимизировать свой выигрыш, а игрока II — минимизировать свой проигрыш. Платежная матрица имеет следующий вид:

I \ II B₁ B₂ ... B_j ... B_n

A₁ a₁₁ a₁₂ ... a_1j ... a_1n ₁

A₂ a₂₁ a₂₂ ... a_2j ... a_2n ₂

... ... ... ... ... ... ... ...

A_i a_i1 a_i2 ... a_ij ... a_in _i

... ... ... ... ... ... ... ...

A_m a_m1 a_m2 ... a_mj ... a_mn _m

Β_j ₁ ₂ ... _j ... _n

Задача состоит в определении:

1. наилучшей (оптимальной) стратегии игрока I из стратегий A₁, A₂, ..., A_m;

2. наилучшей (оптимальной) стратегии игрока II из стратегий B₁, B₂, ..., B_m.

Для решения задачи применяется принцип, согласно которому участники игры одинаково разумны и каждый из них делает все для того, чтобы добиться своей цели.

Проанализируем последовательно каждую стратегию игрока I. Если игрок I выбирает стратегию А₁, то игрок II может выбрать такую стратегию B_j, при которой выигрыш игрока I будет равен наименьшему из чисел a_1j:

.

Выбирая стратегию A_i, игрок I должен рассчитывать на то, что в результате разумных действий игрока II он не выиграет больше, чем _i. Поэтому игрок I должен выбрать ту стратегию, для которой _i максимально:

.

Величина  — гарантированный выигрыш, который может обеспечить себе игрок I при любом поведении игрока II. Величина  называется нижней ценой игры или максимином, а стратегия А_i игрока I, обеспечивающая получение нижней цены игры, называется максиминной чистой стратегией. При этом игрок I при любом поведении игрока II обеспечивает себе выигрыш, не меньше : _i   (i = 1, 2, ..., m).

Игрок II заинтересован в том, чтобы уменьшить свой проигрыш, т.е. обратить выигрыш игрока I в минимум. Для выбора оптимальной стратегии он должен найти максимальное значение выигрыша в каждом столбце:

.

и среди этих значений выбрать наименьшее: .

Величина  называется верхней ценой игры или минимаксом. Стратегия игрока II, обеспечивающая получение верхней цены игры, называется минимаксной чистой стратегией. Применяя ее, игрок II проиграет не больше  при любых действиях игрока I:

_j   (j = 1, 2, ..., n), причем всегда справедливо неравенство   .

Таким образом, придерживаясь максиминной стратегии A_i, игрок I желает получить выигрыш не менее  не зависимо от действий игрока II, а игрок II, придерживаясь минимаксной стратегии B_j, гарантирует себе проигрыш не больше .

Принцип, диктующий игрокам соответствующих стратегий (максиминной и минимаксной), в теории игр называется принципом минимакса. Этот принцип был впервые сформулирован Дж. фон Нейманом в 1928 году.

Пример 1. Дана платежная матрица. Найти решение игры: определить нижнюю и верхнюю цены игры и минимаксные стратегии:

I \ II B₁ B₂ B₃ B₄ 

A₁ 5 3 8 2 2

A ₂ 1 6 4 3 1

A ₃ 9 5 4 7 4

Β_j 9 6 8 7

Таким образом, нижней цене игры ( = 4) соответствует стратегия A₃ игрока I. Выбирая эту стратегию, игрок I достигнет выигрыша не меньше 4 при любом поведении игрока II. Верхней цене игры ( = 6) соответствует стратегия игрока II — В₂. Эти стратегии являются минимаксными. Если обе стороны будут придерживаться этих стратегий, выигрыш будет равен а₃₃ = 4.

Существуют матричные игры, для которых нижняя цена игры равна верхней, т.е.  = . Такие игры называются играми с седловой точкой.

В этом случае  =  =  называется чистой ценой игры, а стратегии игроков и , позволяющие получить это значение — оптимальными. Пара называется седловой точкой матрицы, так как элемент одновременно является минимальным в i-й строке и максимальным в j-м столбце. Оптимальные стратегии и и чистая цена являются решением игры в чистых стратегиях, т.е. без привлечения механизма случайного выбора.

Пример 2. пусть задана платежная матрица. Найти нижнюю и верхнюю цены игры.

I II B₁ B₂ B₃ 

A₁ 5 1 2 1

A₂ 2 6 2 2

A₃ 3 4 3 3

 5 6 3

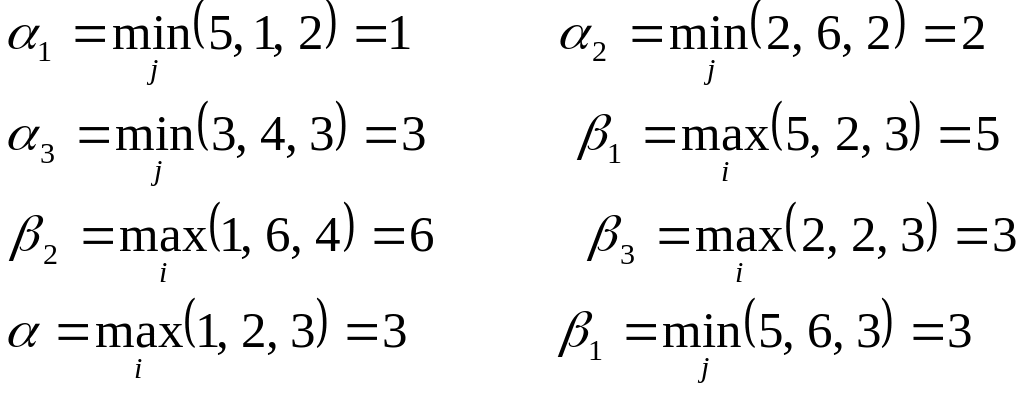
Следовательно  =  =  = 3.

Седловой точкой является пара альтернатив (А₃, В₃).