3.5. Геометрический метод.

Решение игры в смешанных стратегиях допускает наглядную геометрическую интерпретацию. Геометрический метод решения игры включает следующие этапы.

1. В декартовой системе координат по оси абсцисс откладывается отрезок А₁А₂, длина которого равна 1 (рис. 2.1.). Левый конец отрезка точка x = 0 соответствует стратегии A₁, правый, где х = 1,0 — стратегии А₂. Все промежуточные точки этого отрезка соответствуют смешанным стратегиям S₁ = (p₁, p₂).

2. По оси ординат от точки O откладываются выигрыши при стратегии А₁.

3. На линии, параллельной оси ординат, от точки 1 откладываются выигрыши при стратегии А₂ .

Пусть имеется игра с платежной матрицей:

.

Если игрок II применяет стратегию В₁, то выигрыш игрока I при использовании чистых стратегий А₁ и А₂ составляет соответственно a₁₁ = 0,4 и a₂₁ = 0,6. Соединим эти точки прямой В₁В₁ .

Если игрок I при стратегии В₁ применяет смешанную стратегию , то средний выигрыш, определяемый по формуле математического ожидания ₁ = a₁₁p₁ + a₂₁p₂, изображается ординатой точки N на прямой B₁B₁. Прямая B₁B₁ называется стратегией В₁. Ордината любой точки отрезка B₁B₁ равна величине выигрыша игрока I при применении им стратегии A₁ и А₂ с соответствующими вероятностями p₁ и p₂.

Аналогично строим отрезок В₂В₂ , сооветствующий применению игороком II с тратегии В₂ .

Ординаты точек отрезка определяют средний стратегий А₁ и А₂ с соответствующими вероятностями p₁ и p₂ и равных ₂ = a₁₂p₁ + a₂₂p₂.

Пример № 1. Найти оптимальную смешанную стратегию руководителя коммерческого предприятия и гарантированный средний выигрыш при выборе из двух новых технологий продажи товаров и , если известны выигрыши каждого вида продажи по сравнению со старой технологией, которые представлены в виде матрицы игры.

Игрок II Игрок I
	0,4	0,9	0,4
	0,6	0,5	0,5
	0,6	0,9

Решение: находим гарантированный выигрыш определяемый нижней ценой игры которая указывает на максиминную чистую стратегию . Верхняя цена игры что свидетельствует об отсутствии седловой точки, т.к. , тогда цена игры находиться в пределах находим решение игры в смешанных стратегиях геометрическим методам рис. 2.1.

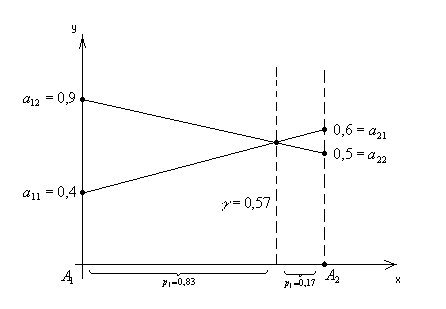
Рис. 2.1. Геометрический метод решения игры

Оптимальная смешанная стратегия и цена игры ровны.

Гарантированный средний выигрыш составляет 0,57.

3.6. Метод линейного программирования.

Антагонистическую игру m  n (где m > 3, n > 3) с конечными значениями m и n можно свести к паре двойственных задач линейного программирования.

Рассмотрим игру m  n, заданную платежной матрицей:

.

При постановке задач, необходимо иметь в виду некоторые преобразования, которые помогают упростить сложную задачу путем изменения – уменьшения размерности платежной матрицы посредством выделения и исключения доминирующих и дублирующих стратегий. Стратегия игрока А_i доминирует над стратегией А_к, если при любом поведении противника даст не меньший выигрыш, а если такой же, то дублирует А_к. В таком случае все элементы i строки больше (доминируют) или равны (дублируют) всех элементов строки k.

Пример. С учетом вариантов конъюнктуры В₁, В₂, В₃, В₄, В₅ сложившейся на рынке и поведения покупателей в микрорайоне города коммерческое предприятие разработало шесть технологий продажи товаров А_1, А_2, А₃, А₄, А₅, А₆. Найти оптимальное решение. Возможные варианты среднедневного товарооборота в млн.руб. приведены в таблице:

	В1	В2	В3	В4	В5
А1	0,4	0,9	0,5	0,5	0,6
А2	0,6	0,5	0,7	0,8	0,9
А3	0,6	0,3	0,8	0,6	0,7
А4	0,3	0,8	0,5	0,4	0,3
А5	0,1	0,3	0,5	0,4	0,3
А6	0,4	0,8	0,5	0,4	0,5

Стратегия А₁ доминирует над стратегией А₆, а стратегия А₄ доминирует над стратегией А₅, следовательно исключаем 5 и 6 строки матрицы

	В1	В2	В3	В4	В5
А1	0,4	0,9	0,5	0,5	0,6
А2	0,6	0,5	0,7	0,8	0,9
А3	0,6	0,3	0,8	0,6	0,7
А4	0,3	0,8	0,5	0,4	0,3

С позиций проигрышей строки В стратегии В_3, В₄ и В₅ доминируют над стратегией В_1, поэтому эти столбцы исключаем из таблицы:

	В1	В2
А1	0,4	0,9
А2	0,6	0,5
А3	0,6	0,3
А4	0,3	0,8

С позиций игрока А стратегия А₁ доминирует над стратегией А₄, а стратегия А₂ доминирует над стратегией А₃, следовательно исключаем 3 и 4 строки матрицы:

	В1	В2
А1	0,4	0,9
А2	0,6	0,5

Допустим, что все элементы (выигрыши) платежной матрицы положительны (a_ij  0) (если это не так, то можно ко всем элементам прибавлять достаточно большое число M, сделав их положительными. При этом цена игры увеличится на M, а решение задачи и не изменится). Если все a_ij  0, то  > 0. Пусть платежная матрица не содержит седловой точки, т.е. игра решается в смешанных стратегиях:

.

Применение игроком I оптимальной смешанной стратегии гарантирует ему средний выигрыш, не меньше цены игры , независимо от поведения игрока II. Игрок II, применяя оптимальную смешанную стратегию гарантирует для себя минимальный проигрыш (не больше ).

Если игрок II применяет свою чистую стратегию B_j, а игрок I — свою оптимальную стратегию , то средний выигрыш игрока I равен:

Если игрок I применяет чистую стратегию А_i, а игрок II – свою оптимальную смешанную стратегии , то средний выигрыш игрока II составит

Учитывая, что _j не может быть меньше  для игрока I, а и не может быть больше  для игрока II, двойственную задачу линейного программирования можно записать следующим образом:

1) для игрока I:

2) для игрока II:

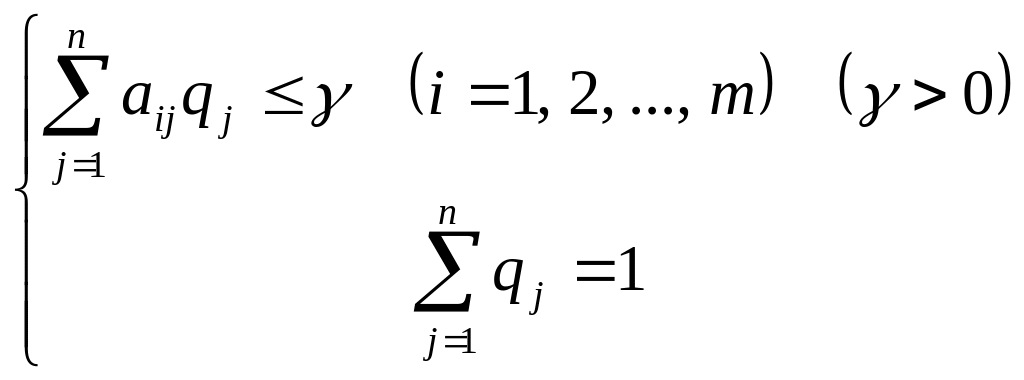
Смысл этих систем уравнений заключается в следующем: игрок I стремится увеличить цену игры (  max), он действует так, чтобы его средний выигрыш при использовании его стратегий с вероятностями p_i для любой j-й стратегии игрока II был не меньше величины , которую он стремится увеличить. Игрок II стремится уменьшить свой проигрыш (  min), т.е. он действует так, чтобы его средний проигрыш при использовании его стратегий с вероятностями q_j при любой i-й стратегии игрока I не превышал величину , которую он стремится уменьшить.

Задача состоит в нахождении двух оптимальных смешанных стратегий и , которые дают для игрока I максимально возможный для него средний выигрыш, а для игрока II минимально возможный для него средний проигрыш.

Разделив левую и правую части неравенств на цену игры  > 0, получим:

Введем обозначения:

Тогда выражения примут следующий вид:

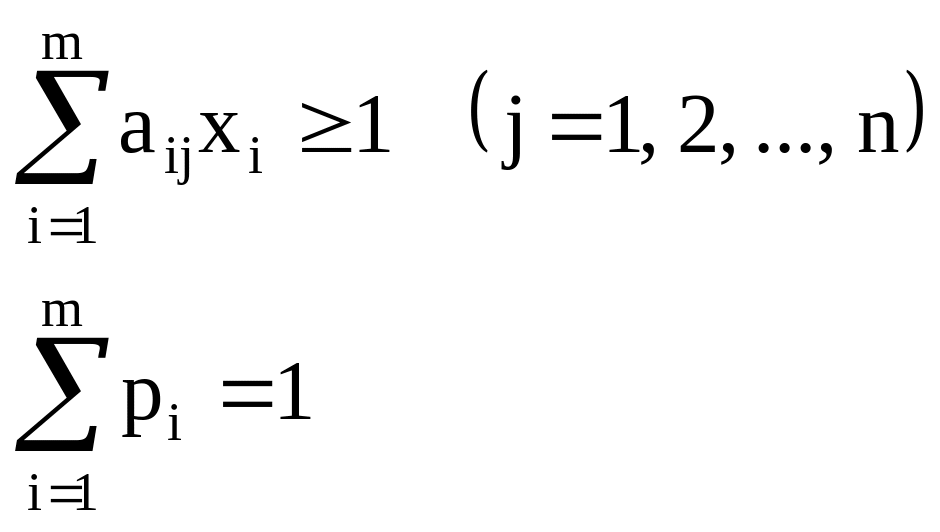
Из равенств и следует, что переменные x_i и y_j должны удовлетворяют условиям:

Учитывая, что игрок I стремится максимизировать , а игрок II стремится минимизировать , переменные x_i и y_j должны быть выбраны так, чтобы целевая функция достигала минимума, а целевая функция достигала максимума.

Таким образом, задача решения игры сводится к задаче линейного программирования. Оптимальные стратегии и игры с платежной матрицей А могут быть найдены путем решения симметричной пары двойственных задач линейного программирования:

Решая их, находим x_i, y_j, цену игры  и оптимальные стратегии и .

или

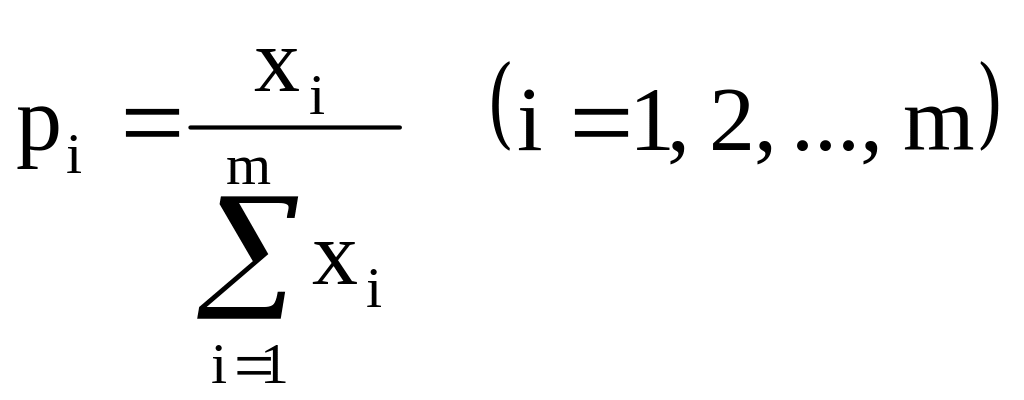
Задача. Найти решение игры конфликтной ситуации с платежной матрицей:

Решение. Математические модели пары двойственных задач линейного программирования можно записать так:

Найти минимум функции F(Х) = x₁ + x₂ + x₃ при ограничениях:

Найти максимум функции Ф(Y) = y₁ + y₂ + y₃ при ограничениях:

Симплексный метод позволяет найти решение этой системы неравенств таблица 2.4.

Тогда цена игры а вероятность применения стратегий игрока II будет:

Таким образом оптимальная система стратегии игрока II.

Таблица 2.4.

Базисные переменные
	1	1	2	3	1	0	0	1
	1	3	1	1	0	1	0
	1	1	3	1	0	0	1	1
	0	-1	-1	-1	0	0	0
		0			1		0
		1			0		0	1
		0			0		1
		0			0		0
		0	0		1
		1	0		0			1
		0	1		0			1
		0	0		0
		0	0	1
		1	0	0
		0	1	0
		0	0	0

Поскольку решение этой системы неравенств симплексным методом дает также и решение табл. 2.4. двойственной задачи.

то находим также и вероятность применения стратегий игрока I:

,

таким образом, оптимальная смешанная стратегия игрока I:

.