
- •Раздел 1:Основы дифференциальной геометрии §1. Векторные функции скалярного аргумента. Предел, непрерывность, производная и интеграл Римана вектор-функции.
- •§2. Кривые в пространстве, длина дуги кривой.
- •§3. Естественный трехгранник линий. Кривизна кривой. Физический смысл кривизны.
- •§4. Формулы Френе. Кручение кривой. Физический смысл кручения.
- •§5. Вычисление кривизны и кручения
- •§6. Параметрические уравнения поверхности. Координатные линии. Касательные векторы гладкой поверхности.
- •§7. Касательная плоскость и нормаль к поверхности
- •§8. Первая квадратичная форма поверхности
- •§9. Площадь поверхности
- •§10. Поверхностный интеграл первого рода: определение, физический смысл, теорема о среднем.
- •§11.Поверхностный интеграл первого рода: теорема о существовании. §12. Поверхностные интегралы второго рода
- •§13.Вычисление поверхностных интегралов второго рода
- •§14. Формула Остроградского-Гаусса
- •§15. Криволинейный интеграл второго рода по пространственной кривой. Вычисление. Примеры. §16. Формула Стокса
- •§17. Теорема о независимости криволинейного интеграла от пути интегрирования.
- •Раздел 2: Теория поля §18. Определение скалярного поля. Примеры. Поверхность уровня, производная по направлению, градиент.
- •§19. Определение векторного поля. Примеры. Векторные линии, векторные поверхности, векторные трубки.
- •§20. Поток векторного поля. Дивергенция. Формула Остроградского-Гаусса в векторной форме.
- •§21. Циркуляция и завихренность векторного поля. Ротор. Формула Стокса в векторной форме.
- •§22. Оператор Гамильтона
- •§23. Потенциальные поля.
- •§24. Соленоидальные поля
- •§25.Ортогональные криволинейные системы координат. Координатные линии и поверхности. Параметры Ламе.
- •§26 .Сферическая и цилиндрическая системы координат: координатные линии, параметры Ламе.
- •1) Цилиндрическая система координат.
- •2) Сферическая система координат.
- •§27.Вычисление градиента и дивергенции в криволинейных координатах
- •§28. Вычисление ротора и оператора Лапласа в криволинейных координатах.
- •§Доп. Дифференциальные операции второго порядка.
- •Раздел 3: Ряды Фурье §29.Ряд Фурье по ортонормированной системе функций, минимальное свойство частичной суммы ряда Фурье, неравенство Бесселя.
- •§30.Тригонометрические ряды Фурье. Ядро Дирихле.
- •§31. Основная лемма теории тригонометрический рядов Фурье.
- •§32. Теорема о представлении кусочно-дифференцируемой функции рядом Фурье
- •§33. Разложение непериодической функции в ряд Фурье на отрезке [-р;р] и [-l; l].
- •§34. Разложение четных и нечетных функций в ряд Фурье, разложение по косинусам и синусам. Примеры.
- •§35. Равномерная сходимость тригонометрического ряда Фурье.
- •§36. Замкнутость и полнота ортогональной системы функций
- •§37. Интеграл Фурье
- •§ 38. Преобразования Фурье
§14. Формула Остроградского-Гаусса
О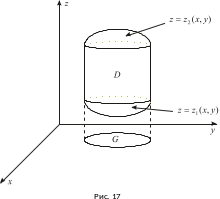 бласть
трёхмерного пространства назовём
z-цилиндрической, если
она ограничена сверху поверхностью
бласть
трёхмерного пространства назовём
z-цилиндрической, если
она ограничена сверху поверхностью
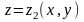 ,
снизу – поверхностью
,
снизу – поверхностью
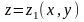 ,
где
,
где
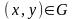 ,
а сбоку - цилиндрической поверхностью
с образующей, параллельной оси z
(см. рис. 17).
,
а сбоку - цилиндрической поверхностью
с образующей, параллельной оси z
(см. рис. 17).
Подобным образом можно определить x-цилиндрические и y-цилиндрические поверхности.
Область назовём простой, если её можно разбить на конечное множество, как x-цилиндрических, так и y-цилиндрических, так и z-цилиндрических поверхностей.
Теорема Остроградского:
Пусть в простой области
,
ограниченной поверхностью
,
определены непрерывные функции
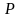 ,
,
 ,
,
 ,
имеющие непрерывные частные производные
,
имеющие непрерывные частные производные
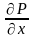 ,
,
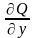 ,
,
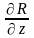 в области
.
Тогда имеет место формула Остроградского:
в области
.
Тогда имеет место формула Остроградского:
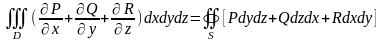 ,
(1)
,
(1)
где нормаль к поверхности внешняя, и искомая поверхность замкнута (например, шар).
Доказательство.
1-й этап.
Рассмотрим интеграл:
 ,
,
где - z-цилиндрическая область. Тогда:
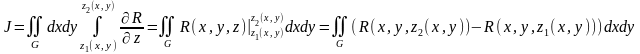 .
.
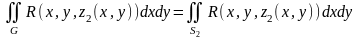 ,
(2)
,
(2)
где
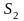 часть поверхности области
,
задаваемая функцией
.
часть поверхности области
,
задаваемая функцией
.
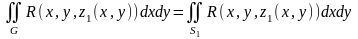 ,
(3)
,
(3)
где
 часть поверхности области
,
задаваемая функцией
.
часть поверхности области
,
задаваемая функцией
.
Обозначим боковую поверхность
через
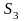 ,
тогда:
,
тогда:
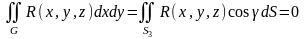 (4)
(4)
Тогда, складывая (2), (3) и (4), получим:
 .
.
Таким образом, формула Остроградского для z-цилиндрической поверхности имеет вид:
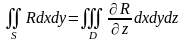 .
.
2-й этап.
Пусть область
простая. Тогда её можно разделить на
конечное множество z-цилиндрических
поверхностей
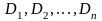 .
Имеем:
.
Имеем:
 ,
(5)
,
(5)
где
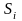 - поверхность области
.
- поверхность области
.
П оверхности
оверхности
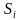 состоят из частей поверхности
и поверхностей, которыми разделена
область
на области
состоят из частей поверхности
и поверхностей, которыми разделена
область
на области
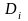 .
Поделы входят в состав двух поверхностей
,
причём с разными знаками, следовательно
при интегрировании по этим частям знаки
интегралов будут противоположными, а
модули совпадать, значит при суммировании
они взаимно уничтожатся. Следовательно,
имеем:
.
Поделы входят в состав двух поверхностей
,
причём с разными знаками, следовательно
при интегрировании по этим частям знаки
интегралов будут противоположными, а
модули совпадать, значит при суммировании
они взаимно уничтожатся. Следовательно,
имеем:
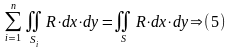
Значит формула (5) справедлива для всякой простой области, ограниченной кусочно-регулярной поверхностью.
3-й этап.
Аналогично доказываются равенства:
 (6)
(6)
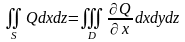 (7)
(7)
4-й этап.
Складывая (5),(6),(7), получим формулу (1), что и требовалось доказать.
Замечание.
Формула Остроградского-Гаусса может
быть использована для вычисления объёма
тела, ограниченного поверхностью
(где
- регулярная поверхность). Поскольку
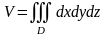 ,
то из формулы Остроградского-Гаусса
следует:
,
то из формулы Остроградского-Гаусса
следует:
 ,
,
если
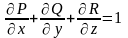 ,
,
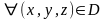 .
Чаще всего на практике используют
следующую формулу:
.
Чаще всего на практике используют
следующую формулу:
![]() .
.
§15. Криволинейный интеграл второго рода по пространственной кривой. Вычисление. Примеры. §16. Формула Стокса
Рассмотрим двухстороннюю поверхность S, заданную следующим уравнением:
,
где
![]() .
Данная поверхность ограниченна некоторой
кусочно-гладкой линией
.
Данная поверхность ограниченна некоторой
кусочно-гладкой линией![]() .
.
Обход поверхности
![]() по контуру
называется согласованным с выбранной
стороной поверхности, если наблюдатель,
двигаясь по выбранной стороне поверхности
вдоль контура
,
видит поверхность слева, и нормаль при
этом направлена вверх.
по контуру
называется согласованным с выбранной
стороной поверхности, если наблюдатель,
двигаясь по выбранной стороне поверхности
вдоль контура
,
видит поверхность слева, и нормаль при
этом направлена вверх.
Пусть в области D содержится
регулярная поверхность S
со своей границей, и пусть в области
заданы функции
![]() ,
,
![]() ,
,
![]() ,
непрерывные вместе со своими частными
производными первого порядка. Тогда
имеет место формула Стокса:
,
непрерывные вместе со своими частными
производными первого порядка. Тогда
имеет место формула Стокса:
 .
(1)
.
(1)
Причём в данной формуле обход контура согласован со стороной поверхности S.
Доказательство.
Рассмотрим интеграл по поверхности :
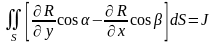 .
(2)
.
(2)
Переходя к координатам
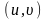 ,
имеем:
,
имеем:
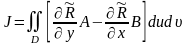 (3)
(3)
где
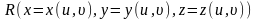 ,
коэффициенты
и
- якобианы, причём:
,
коэффициенты
и
- якобианы, причём:
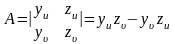 ,
(4)
,
(4)
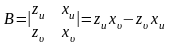 .
(5)
.
(5)
Подставляя (4) и (5) в (2), имеем:
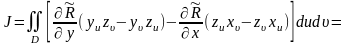
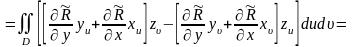
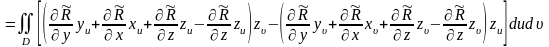 .
.
Так как,
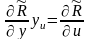 ,
,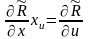 ,
,
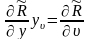 ,
,
 ,
имеем:
,
имеем:
 .
.
Согласно формуле Грина имеем:
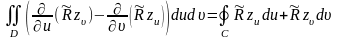 ,
,
где ограничивает область .
Учитывая, что контур
с помощью отображения
отображается в границу
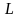 поверхности
,
то так как
поверхности
,
то так как
 ,
имеем:
,
имеем:
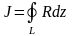 .
.
То есть, согласно (2) получили:
 .
(6)
.
(6)
Аналогично получаем выражения
 ,
(7)
,
(7)
 .
(8)
.
(8)
Складывая (2),(3),(4) получаем:
,
что и требовалось доказать.
