Билет №1

Задание 1

Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

(1)

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Определение. Решение системы уравнений — это последовательность чисел (k₁, k₂, ..., k_n), которая является решением каждого уравнения системы, т. е. При подстановке в это уравнение вместо переменных x₁, x₂, ..., x_n дает верное числовое равенство.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c₁⁽¹⁾ = c₁⁽²⁾, c₂⁽¹⁾ = c₂⁽²⁾, …, c_n⁽¹⁾ = c_n⁽²⁾.

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Метод Гаусса — точный метод решения систем линейных алгебраических уравнений.

Метод Гаусса (его еще называют методом гауссовых исключений) состоит в том, что совместную систему n линейных алгебраических уравнений относительно n неизвестных (определитель матрицы системы отличен от нуля)

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

решение которой находят по рекуррентным формулам

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными преобразованиями над строками приводят расширенную матрицу системы к ступенчатому виду:

а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась диагональная матрица

В результате получаем решение системы:

Опишем метод Гаусса последовательно.

Прямой ход

Рассмотрим расширенную матрицу системы

1-й шаг

Предположим, что a₁₁ не равен 0.

Если это не так, и a₁₁ = 0, переставим строки матрицы так, чтобы a₁₁ не был равен 0. Это всегда возможно, т.к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна.

Элемент a₁₁ (не равный 0) называется ведущим элементом.

Итак, a₁₁ не равно 0.

Умножим первую строку на число и прибавим ко второй строке, затем умножим первую строку на число и прибавим к третьей строке, и т.д., т.е. последовательно умножаем первую строку на число и прибавляем к i-й строке, для i=2, 3, …, n.

Получим на первом шаге:

.

2-й шаг

Предположим, что a⁽¹⁾₂₂ не равен 0.

Если это не так, и a⁽¹⁾₂₂ = 0, переставим строки матрицы так, чтобы a⁽¹⁾₂₂ не был равен 0.

Здесь ведущий элемент a₂₂ (е равный 0).

Умножим вторую строку на число и прибавим к третьей строке, затем умножим вторую строку на число и прибавим к четвертой строке, и т.д., т.е. последовательно умножаем вторую строку на число и прибавляем к i-й строке, для i=3, 4, …, n.

Получим на втором шаге:

k-й шаг

Предположим, что a^(k-1)_kk не равен 0.

Если это не так, и a^(k-1)_kk = 0, переставим строки матрицы так, чтобы a^(k-1)_kk не был равен 0.

Ведущий элемент a^(k-1)_kk) не равный 0).

Умножим k-ю строку на число и прибавим к i-й строке, для i=k+1, k+2, …, n.

Выполнив n-1 шаг получим:

.

Прямой ход закончен. Заметим, что все элементы на главной диагонали отличны от нуля.

Обратный ход

1-й шаг.

Умножим последнюю строку на число и прибавим к предпоследней строке, затем умножим последнюю строку на число и прибавим к (n-2)-й строке, и т.д., т.е. последовательно умножаем последнюю строку на число и прибавляем к (n-i)-й строке, для i=1, 3, …, n-1.

Получим на первом шаге:

.

k-й шаг

Умножим k-ю строку на число и прибавим к i-й строке, для i=k-1, k-2, …, n-1.

Выполнив n-1 шаг получим:

Обратный ход закончен. Решение вычисляем по формулам:

Система

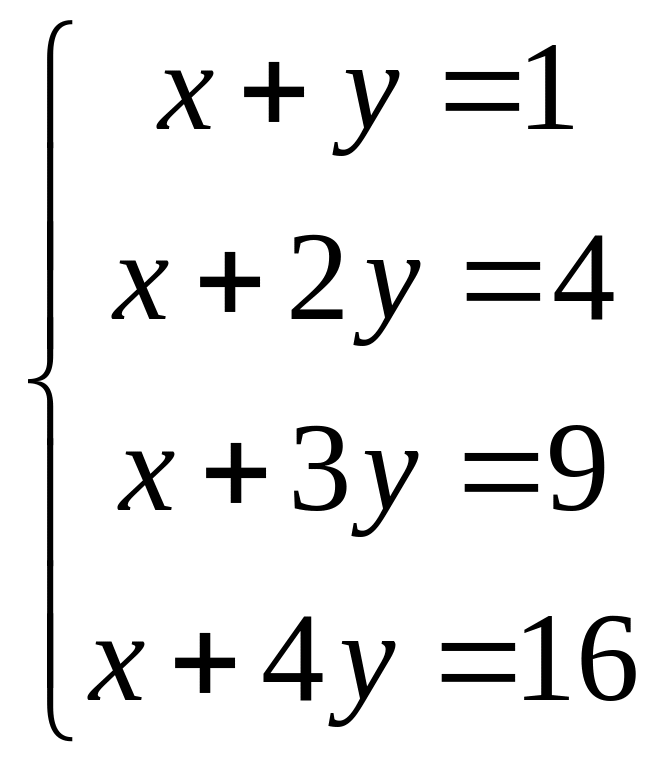
Для того, что бы узнать, совместна ли она, надо узнать, имеет ли она решения.

Самы простой способ — решить систему. Для этого выразим из первого уравнения x : x = 1 – y

и подставим в остальные уравнения, получим:

Отсюда видно, что решений нет. Значит система не совместна.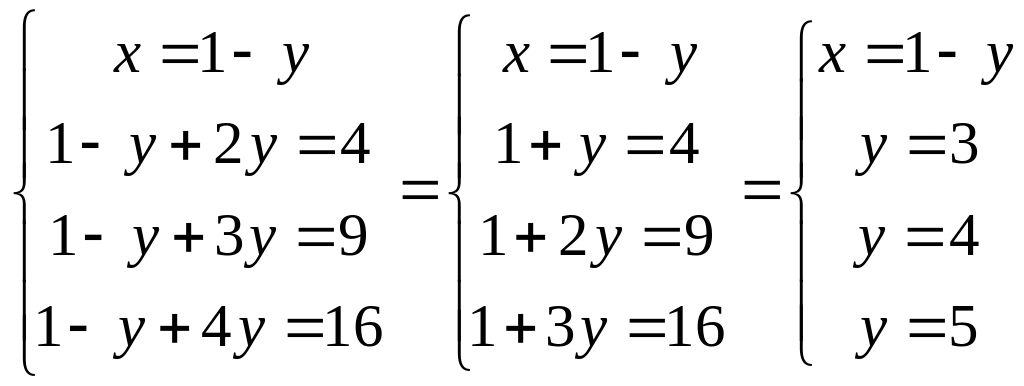

Задание 2

Гиперплоскость — подпространство коразмерности 1 в векторном, аффинном пространстве или проективном пространстве; то есть подпространство с размерностью, на единицу меньшей, чем объемлющее пространство.

Например, для двумерного пространства гиперплоскость есть прямая, для трёхмерного — плоскость и т. д.

Уравнение гиперплоскости

Пусть — нормальный вектор к гиперплоскости, тогда уравнение гиперплоскости, проходящей через точку , имеет вид

Здесь — скалярное произведение в пространстве . В частном случае уравнение принимает вид

Расстояние от точки до гиперплоскости

Пусть — нормальный вектор к гиперплоскости, тогда расстояние от точки до этой гиперплоскости даётся формулой

где — произвольная точка гиперплоскости.

Задание 3

Билет №2

Задание 1

Однородная система уравнений — это система уравнений, в которой у каждого уравнения свободный член равен нулю.

Решается по-моему так же, как и для обычных систем.

Решение системы

очевидно, что (0,0,0,0) — будет решением системы

Второе будет (0,1,2,1) (внимательно посмотрел на уравнения)

Третье будет (1,2,1,0) (внимательно посмотрел на уравнения)

Задание 2

Параметрические уравнения прямой могут быть записаны в виде:

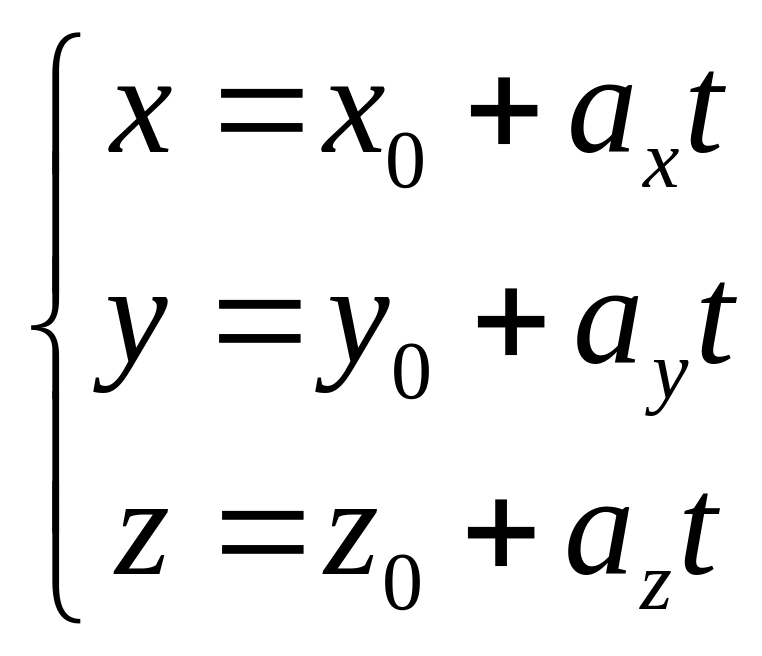
где t — производный параметр, a_x, a_y и a_z — координаты x и y направляющего вектора прямой.

Смысл параметра t аналогичен параметру в векторно-параметрическом уравнении.

Расстояние от точки до прямой

, где x,y,z — координаты точки.

Задание 3

Билет №3

Задание 1

Зададим в (действительном или комплексном) систему из векторов

                                                                                        (1)

По определению, система (1) линейно независима, если из векторного равенства

,                                                                                                                  (2)

где , , ..., - числа (соответственно действительные или комплексные), следует, что

.

Геометрический смысл

• Векторы и линейно зависимы тогда и только тогда, когда они коллинеарны (лежат на параллельных прямых).

• Векторы линейно зависимы тогда и только тогда, когда они компланарны (лежат в одной плоскости).

Задание 2

Прямоугольная (Декартова) система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.

Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: .

Окта́нт ― любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями.

Расчет их ведется в следующем порядке: I, II, III и IV – с левой стороны от профильной плоскости, а V, VI, VII, VIII – с правой.

• I (+, +, +)

• II (+, −, +)

• III (+, −, −)

• IV (+, +, −)

• V (−, +, +)

• VI (−, −, +)

• VII (−, −, −)

• VIII (−, +, −)

Задание 3

Ненулевой вектор называется собственным вектором линейного оператора , если ( для комплексного ), такое, что Число называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.

Для оператора с матрицей:

Собственное значение равно 2

собственные вектора равны

(0.866;0,5)

(-0.5;0.866)

Билет №4

Задание 1

лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции y = kx) на случай более общего множества аргументов и значений. Линейные операторы, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.

Или иначе

Лине́йным оператором векторного пространства L_K над полем K в векторное пространство M_K (лине́йным опера́тором из L_K в M_K) над тем же полем K называется отображение

,

удовлетворяющее условию линейности

f(x + y) = f(x) + f(y),

f(αx) = αf(x).

для всех и .

Для нахождения характеристических чисел и собственных векторов оператора выберем произвольно базис в . Пусть и — матрица, отвечающая оператору в базисе . Тогда, приравнивая между собой соответственные координаты векторов, стоящих в левой и правой частях равенства (53), получим систему скалярных уравнений

                       (54)

которую можно записать и так:

                 (55)

Так как искомый вектор не должен быть равен нулю, то среди его координат по крайней мере одна координата должна быть отлична от нуля.

Для того чтобы система линейных однородных уравнении (55) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю:

.                    (56)

Уравнение (56) представляет собой алгебраическое уравнение -й степени относительно . Коэффициенты этого уравнения принадлежат тому же числовому полю, что и элементы матрицы т. е. полю .

Уравнение (56) часто встречается в различных проблемах геометрии, механики, астрономии, физики и носит название характеристического уравнения или векового уравнения матрицы (левую часть этого уравнения называют характеристическим многочленом).

Таким образом, каждое характеристическое число линейного оператора является корнем характеристического уравнения (56). И наоборот, если некоторое число является корнем уравнения (56), то при этом значении система (55) и, следовательно, (54) имеет ненулевое решение т. е. этому числу отвечает собственный вектор оператора м.

Задание 2

Симплекс или n-мерный тетраэдр (от лат. Simplex — простой) — геометрическая фигура, являющаяся n-мерным обобщением треугольника. Ещё известна как простейшая фигура n-мерного пространства (0_о)

Симплекс есть выпуклая оболочка n+1 точек, не лежащих в одной гиперплоскости n-мерного Евклидова пространства. Эти точки называются вершинами симплекса.

Симплекс называется правильным, если все его рёбра имеют одинаковую длину.

Зелёный треугольник — стандартный 2-симплекс

Стандартный n-симплекс это подмножество , определяемое как:

Его вершинами являются точки:

e₀=(1, 0, … 0)

e₁=(0, 1, … 0)

…

e_n=(0, 0, … 1)

Существует каноническое взаимно-однозначное отображение стандартного n-симплекса в любой другой n-симплекс с координатами вершин :

Значения t_i для данной точки называются её барицентрическими координатами.

Задание 3

Билет №5

Задание 1

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.