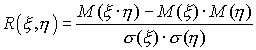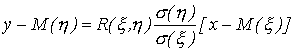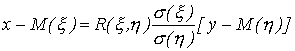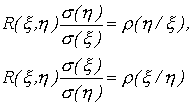§ 9. Элементы теории корреляций. 2. Коэффициент корреляции. Как мы знаем, если и - независимые случайные величины, то по свойству математического ожидания (§ 4, п. 1)

(72)

   Если же и не являются независимыми случайными величинами, то, вообще говоря,  

   Условились за меру связи (зависимости) двух случайных величин и принять безразмерную величину , определяемую соотношением.

(73)

   и называемую коэффициентом корреляции.    Рассмотрим некоторые свойства коэффициента корреляции.    Если и - независимые случайные величины, то коэффициент корреляции равен нулю.    Это свойство непосредственно вытекает из соотношений (72) и (73). Заметим, что обратное утверждение, вообще говоря, неверно, т. е. если , то отсюда еще не следует, что и независимы.    Заметим без доказательства, что . При этом если , то между случайными величинами и имеет место функциональная, а именно линейная зависимость.    Замечание. Как мы видели (§ 3, п. 6), двумерная случайная величина распределена нормально, если плотность распределения системы величин и имеет вид  

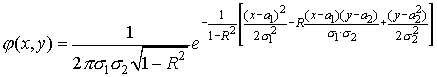
   Можно показать, что постоянная R равна коэффициенту корреляции величин и , т.е. . Следует заметить, что в случае, когда система величин и распределена нормально и коэффициент корреляции , то величины и

9. Элементы теории корреляций. 3. Функции и линии регрессии.

    Пусть и - две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значению x случайной величины соответствует вполне определенное распределение вероятностей величины . Плотность распределения величины при условии, что , называется условной плотностью распределения случайной величины .    Вычислим для данного случая так называемое условное математическое ожидание величины при условии, что . Согласно определению математического ожидания непрерывной случайной величины, имеем

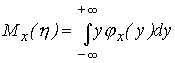
[см. формулу (40)]. Каждому возможному значению x случайной величины соответствует определенное значение условного математического ожидания . Таким образом, мы получаем функцию переменной x. Эта функция y=f(x) называется функцией регрессии величины на , а ее график - линией регрессии на .    Аналогично определяется условное математическое ожидание величины при условии, что :

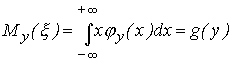
где - условная плотность вероятности случайной величины при условии, что .    Функция x=g(y) называется функцией регрессии величины на , а ее график - линией регрессии на .    Cледует иметь в виду, что функции y=f(x) и x=g(y) не являются обратными по отношению друг к другу.    Если обе функции и линейны, то линиями регрессии являются прямые. В этом случае говорят, что случайные величины и связаны линейной корреляционной зависимостью. Можно показать, что уравнение прямой регрессии на имеет следующий вид:

(74)

где - условное математическое ожидание случайной величины при . Аналогично записывается уравнение прямой регрессии на :

(75)

где - условное математическое ожидание случайной величины при .    Величины

(76)

называются коэффициентами регрессии соответственно на и на .    Из формул (76) следует, что

(77)

Равенство (77) показывает, что оба коэффициента регрессии имеют одинаковые знаки. Если они положительны (отрицательны), то с возрастанием аргумента возрастают (убывают) соответствующие условные математические ожидания.    Если , то, как следует из уравнений (74) и (75), и , т.е. в этом случае условные математические ожидания постоянны и равны соответствующим математическим ожиданиям случайных величин и .    Замечание. Можно доказать, что если система двух случайных величин имеет нормальное распределение, то эти величины находятся в линейной корреляционной зависимости.

Доверительный интервал

До сих пор мы находили различные числовые характеристики выборки, которые определяются одним числом. Такие оценки называются точечными. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. Поэтому для небольших выборок следует пользоваться интервальными оценками. Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальная оценка позволяет установить точность и надежность оценок, а сами интервалы в этом случае называются доверительными.

         Доверительным интервалом называется интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью α.

         В педагогике наиболее распространенным является оценка математического ожидания a случайной величины X, распределенной по нормальному закону, при известном среднем квадратическом отклонении σ.  В этом случае для оценки математического ожидания a служит интервал:

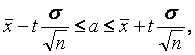
где  – точность оценки, n – объём выборки,   – выборочное среднее, t – аргумент функции Лапласа, при котором .

         Рассмотрим пример. Пусть среднее квадратическое отклонение σ нормально распределенного признака X генеральной совокупности равно 5, объём выборки n равен 100 и выборочное среднее . Найдем доверительный интервал математического ожидания a при α=0,9.

         Все величины, кроме t, известны. Найдем t по специальной таблице, исходя из соотношения  Получим, что t=1,65, следовательно:

 

или 19,175≤a≤20,825.

         Таким образом, можно сделать вывод о том, что математическое ожидание генеральной совокупности с вероятностью α=0,9 окажется внутри полученного интервала.

         Во многих педагогических задачах требуется установить и оценить зависимость одной случайной величины от другой. Две случайные величины могут быть связаны функциональной зависимостью, что случается крайне редко, либо зависимостью другого рода, называемой статистической, либо быть независимыми.

         Статистической называется зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется выборочная средняя другой. В этом случае статистическую зависимость называют корреляционной.

Если число испытаний n в схеме независимых испытаний Бернулли растет, а вероятность p уменьшается, то точная формула практически непригодна из-за громоздких вычислений и возникающих погрешностей округления. В этом случае пользуются приближенными формулами Пуассона (при npq < 9) и Муавра-Лапласа (npq > 9).

 

Теорема Пуассона

 

Если число испытаний n в схеме независимых испытаний Бернулли стремится к бесконечности и так, что , , то при любых

Это означает, что при больших n и малых p вместо громоздких вычислений по точной формуле можно воспользоваться приближенной формулой

, т.е. использовать формулу Пуассона для  = np.

На практике пуассоновским приближением пользуются при npq < 9.

 

Локальная теорема Муавра-Лапласа

Пусть 0< p <1 и величина при n  ограничена. Тогда .

На практике приближением Муавра-Лапласа пользуются при npq > 9.

Точность формулы 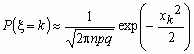растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.

 

Интегральная теорема Муавра-Лапласа

 

Пусть 0< p <1, тогда для схемы Бернулли при n  для любых a и b справедлива формула

.

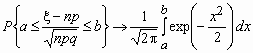Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

,

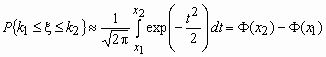где , , 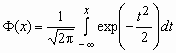- функция Лапласа.

Точность этой приближенной формулы растет с ростом n.

Если npq сравнительно невелико, то лучшее приближение дает формула

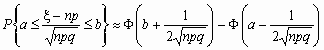
и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

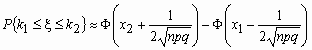, где , .

Теорема Бернулли

 

Если  - число успехов в n испытаниях Бернулли с вероятностью успеха в одном испытании p, 0 < p < 1, то для любого  > 0 справедливо: .

Утверждение теоремы Бернулли означает, что с ростом числа испытаний n относительная частота успехов  /n приближается к вероятности p успеха в одном испытании.

Достаточно часто возникает необходимость установить, сколько нужно произвести испытаний, чтобы отклонение относительной частоты успехов  /n от вероятности p с вероятностью, больше или равной было меньше . Т.е. требуется найти n, для которого справедливо неравенство . Доказано, что число n, которое обеспечивает выполнение этого неравенства, удовлетворяет соотношению 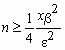, где - решение уравнения . Следует обратить особое внимание на замечательный факт: искомое значение n не зависит от p!