9.3 Векторное произведение векторов
9.3.1 Правая и левая система координат
Три некомпланарных вектора , , , взятых в указанном порядке называют тройкой векторов. Пусть векторы , и отложены из одной точки. Будем смотреть с конца вектора на плоскость, в которой лежат векторы и . Если кратчайший поворот от к совершается против часовой стрелки, то тройка векторов , , называется правой тройкой (рисунок 9.2). Если же указанный поворот совершается по часовой стрелке, то тройка векторов , , называется левой (рисунок 9.3).
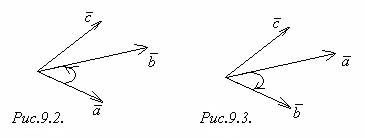
Рисунок 9.2
Рисунок 9.3
Декартовая прямоугольная система координат Охуz называется правой, если тройка её базисных векторов является правой, и левой, если тройка – левая. В основном используют правые прямоугольные системы координат.
9.3.2 Векторное произведение векторов
Определение 9.2. Векторным произведением вектора на вектор называется вектор × , который удовлетворяет следующим условиям:
1) │ × │ = │ ││ │sinφ, где φ – угол между векторами и ;
2) вектор × перпендикулярен каждому из векторов и ;
3) тройка векторов , , × – правая.
Свойства векторного произведения
1. × = 0 для любого вектора .
2. Векторы и коллинеарны тогда и только тогда, когда × = 0.
3. Площадь параллелограмма, построенного на неколлинеарных векторах и , равна │ × │.
4. Площадь
треугольника, построенного на
неколлинеарных векторах
и
,
равна
│
×
│.
5. × = – ( × ).
6. ( + )× = × + × .
7. ( α) × ( β) = ( × )(αβ).
Теорема 9.2. Если = (х1; у1; z1) и = (х2; у2; z2), то
×
=
=
−
+
.
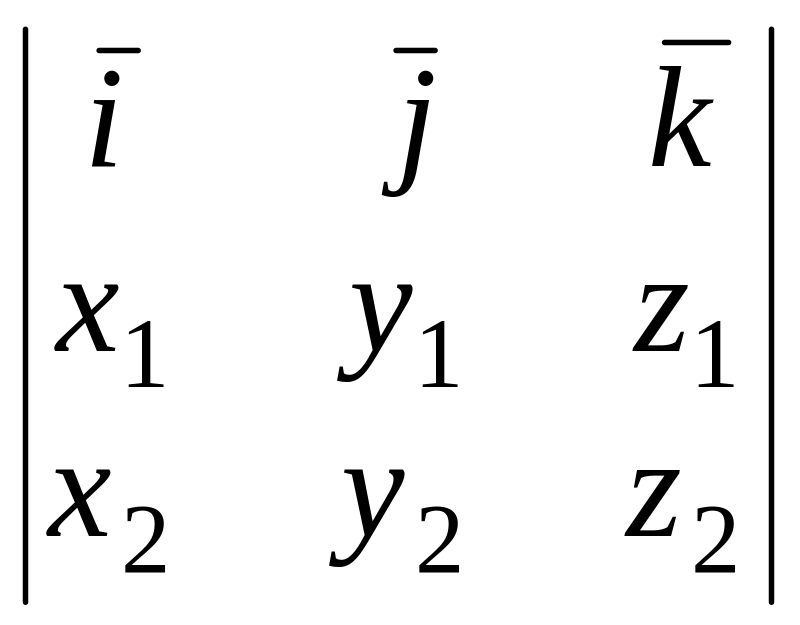Доказательство. Запишем разложение векторов и по базисным векторам:
= + + , = + + .
Составим таблицу векторных произведений базисных векторов, используя рисунок 9.4:
|
|
|
|
|
|
|
- |
|
- |
|
|
|
|
- |
|
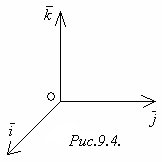
Рисунок 9.4
Теперь
×
=
(
+
+
)
× (
+
+
)
(
)×(
)
+ (
)×(
)
+ (
)×(
)
+ + (
)×(
)
+ (
)×(
)
+ (
)×(
)
+ (
)×(
)
+ (
)×(
)
+ (
)×(
)
(
×
)
+(
×
)
+(
×
)
+(
×
)
+(
×
)
+(
×
)
+ (
×
)
+
+(
×
)
+(
×
)
−
(
)+
(
)+
(
)−
(
)−
(
)+
(
)
= =
(
−
)−
(
−
)+
(
−
)
=
−
+
=
.
Следствие 9.3. Площадь параллелограмма, построенного на неколлинеарных векторах = (х1; у1; z1) и = (х2; у2; z2) равна модулю векторного произведения × , т. е.
Sпаралл.
= │
×
│=
.
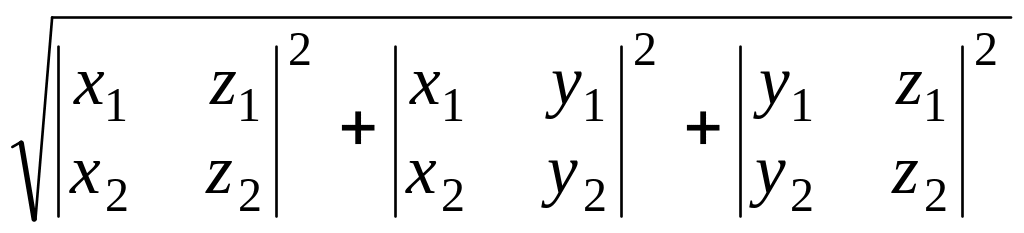Следствие 9.4. Площадь треугольника, построенного на неколлинеарных векторах = (х1; у1; z1) и = (х2; у2; z2) вычисляется по формуле
Sтреуг. = .
Пример. Найти площадь треугольника АВС, если А(–1; –1; 1), В(1; –3; 4), С(3; –1; –5).
Решение. Найдём
координаты векторов
и
:
=
(2; –2; 3),
= (4; 0; –6). Тогда
×
=
=
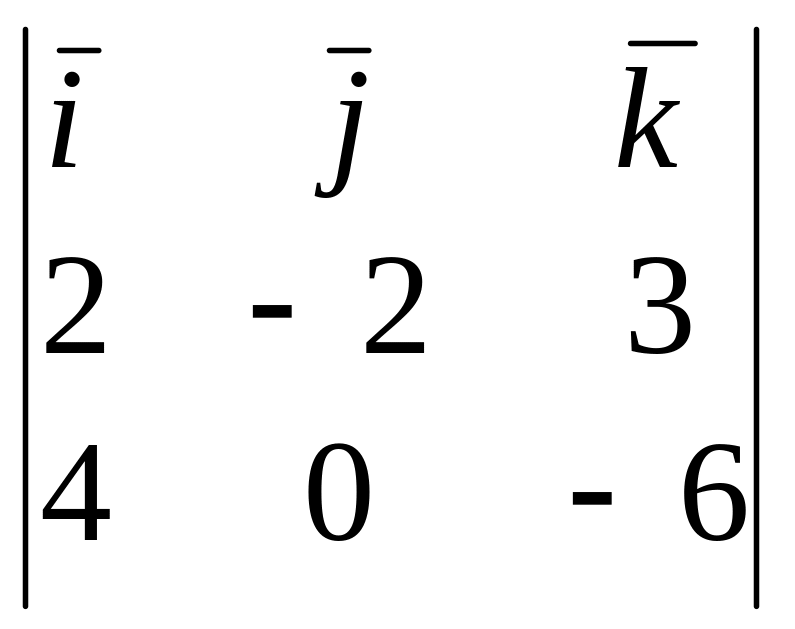12
+
24
+
8,
т. е.
×
= (12; 24; 8).
Следовательно,
SABC
=
│
×
│=
= 14. (кв. ед.).
Ответ: 14.