Распределение Пуассона

Для n > 30 производить расчеты по формуле Бернулли становится затруднительным из-за слишком больших величин факториалов, поэтому используют асимптотические формулы Пуассона и Лапласа, которые становятся все более и более точными с увеличением n (именно в тех случаях, когда расчеты по исходной формуле Бернулли практически невозможны). Формула Пуассона применяется для больших n > 30 и малых р < 0,05, таких, что nр < 5 (поэтому распределение Пуассона применяется для изучения распределения количества редких событий). Во всех остальных случаях (n > 30, nр  5, nq  5) применяется асимптотическая формула Лапласа. Например, представим себе партию электролампочек, из которых 2% выходит из строя при перевозке. Какова вероятность того, что число испорченных лапмпочек будет не больше 5? Если перевозится n = 10 лампочек, то расчеты вероятностей надо производить по формуле Бернулли; если в партии n = 100 лампочек – расчеты надо производить по формуле Пуассона (n = 100 > 30; р = 0,02 < 0,05; nр = 2 < 5); если же в партии n = 1000 лампочек – расчеты надо производить уже по формуле Лапласа (n = 1000 > 30; nр = 20 > 5; nq = 980 > 5).

Закон распределения редких событий Пуассона

имеет самостоятельное значение и свою область применения – теорию массового обслуживания. Получим вышеприведенное выражение как предельную формулу для распределения Бернулли при n  , р  0, q  1, но при этом nр = а = Const.

Преобразуем формулу Бернулли:

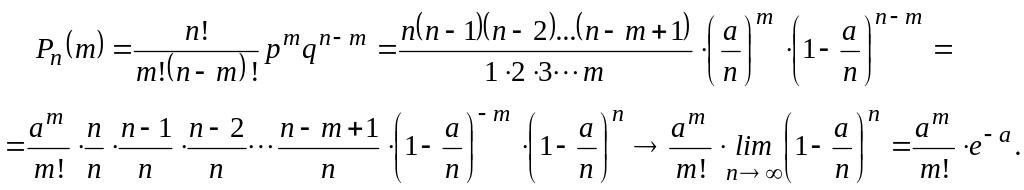
Поскольку формулу Пуассона можно рассматривать как предельный случай формулы Бернулли, то для нее сохранились все характеристики р аспределения Бернулли с заменой р  0, q  1, np = a: (a – 1)  Mo  a; M(m) = a; D(m) = a; .

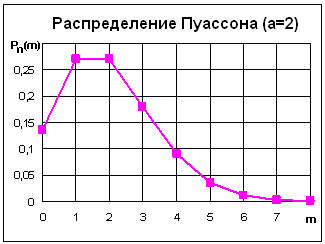
Распределение Пуассона зависит от одного параметра а. Типичный вид полигонов распределения Пуассона для разных значений параметра а показан на рис. 4.4, из которого видно, что с увеличением а вид распределения прибли­жается к стандартной симметричной форме (распределению Лапласа).

Вычисления вероятностей P(m) распределения Пуассона удобно производить по реккурентной формуле: , где Р(0) = е^–а .

Например, для а = 2: Р(0) = е^–2 = 0,135; Р(1) = Р(0)²/₁ = 0,270; Р(2) = Р(1)²/₂ = 0,270; Р(3) = Р(2)²/₃ = 0,180; Р(4) = Р(3)²/₄ = 0,090; и т.д.

Обычно в задачах на распределение Пуассона задается среднее число появления некоторого события за определенный период времени: a = t, где  – "интенсивность появления события" – среднее число событий в единицу времени.

Для примера рассмотрим следующую задачу.

В одном кубичном метре воздуха в среднем находится 1000 болезнетворных микробов. На анализ взяли 2 литра (дм³) воздуха. Найти вероятность того, что в пробе будет выявлено m = 0, 1, 2, ... болезнетворных микробов, не больше трех микробов, от двух до пяти микробов, хотя бы один микроб.

Решение. Это типичная задача на распределение Пуассона, где задана интенсивность  = 1000 для t = 1 м³; для t = 2 л = 0,002 м³ получаем а = 10000,002 = 2 – это среднее количество микробов в 2-х литрах воздуха.

Вместо использования формулы Пуассона вычисления вероятностей производим по реккурентным формулам:

.

Возможные значения m не ограничены сверху, однако, согласно правилу "трех сигм", достаточно рассчитать вероятности P(m) только для .

Для m = 0, 1, 2, ..., 10 вычисления сведены в таблицу, рядом с ней построен график полигона.

С помощью функции F(m) находим: P(m  3) = F(3) = 0,857123; P(2m5) = F(5) – F(1) = 0,983436 – 0,406006 = 0,57743; P(m1) = 1 – P(0) = = 1 – 0,135335 = 0,864665.

Определяем характеристики распределения Пуассона:

M(m) = a = 2; D(m) = a = 2; .

a – 1  Mo  a; 1  Mo  2; P(1) = P(2) = P_max.

Здесь целочисленны оба края интервала длиной единица, поэтому самыми вероятными оказались сразу два соседних значения.

m	P(m)	F(m)	Рис. 4.5. Полигон распределения Пуассона
0	0,135335	0,135335
1	0,270671	0,406006
2	0,270671	0,676676
3	0,180447	0,857123
4	0,090224	0,947347
5	0,036089	0,983436
6	0,012030	0,995466
7	0,003437	0,998903
8	0,000859	0,999763
9	0,000191	0,999954
10	0,000038	0,999992