
- •Лекция 1. Основные понятия теории вероятности
- •Вопросы для самопроверки
- •Лекция 2. Теоремы о вероятностях
- •Теорема умножения вероятностей
- •Краткая классификация событий
- •Теорема о полной вероятностей
- •Теорема (формула) Байеса
- •Теорема сложения вероятностей
- •Принцип практической невозможности редких событий
- •Вопросы для самопроверки
- •Лекция 3. Случайные величины
- •Дискретная случайная величина
- •Числовые характеристики случайных величин
- •Характеристики положения
- •Характеристики разброса
- •Характеристики формы
- •Свойства математического ожидания
- •Свойства дисперсии
- •Правило "3-х сигм"
- •Вопросы для самопроверки
- •Лекция 4. Распределение Бернулли, Пуассона, Лапласа Распределение Бернулли
- •Биномиальные коэффициенты
- •Распределение Пуассона
- •Вопросы для самопроверки
- •Лекция 5. Распределение Лапласа
- •И нтегральная теорема Лапласа
- •Три основных формы интегральной теоремы Лапласа
- •Вопросы для самопроверки
- •Лекция 6. Непрерывная случайная величина
- •Нормальный закон распределения Гаусса
- •Показательный или экспоненциальный закон распределения
- •Квантили распределения
- •Вопросы для самопроверки
- •Лекция 7. Предельные теоремы теории вероятностей
- •Закон больших чисел
- •Центральная предельная теорема
- •Композиция распределений случайных величин
- •Функции случайного аргумента
- •Вопросы для самопроверки
- •Лекция 8. Система случайных величин
- •Закон распределения дискретной двумерной случайной величины
- •Характеристики дискретной двумерной случайной величины
- •Закон распределения непрерывной двумерной случайной величины
- •Характеристики непрерывной двумерной величины
- •Двумерный нормальный закон
- •Вопросы для самопроверки
- •Лекция 9. Проблемы математической статистики
- •Способы составления выборочных подсовокупностей
- •Статистичекое оценивание
- •Вопросы для самопроверки
- •Лекция 10. Свойства статистических оценок
- •Оценка параметров распределения
- •Статистические критерии
- •Вопросы для самопроверки
- •Лекция 11. Критерии согласия Критерий согласия Пирсона
- •Критерий согласия Колмогорова – Смирнова
- •Интервальные оценки характеристик и параметров
- •Вопросы для самопроверки
- •Лекция 12. Проверка статистических гипотез Распределение Стьюдента
- •Интервальная оценка для математического ожидания
- •Проверка гипотезы о равенстве центров двух совокупностей
- •Сравнение двух дисперсий
- •Вопросы для самопроверки
- •Лекция 13. Дисперсионный анализ
- •Ранговый дисперсионный анализ Краскала–Уоллиса
- •Время появления реакции в 4-х группах
- •Ранжированнае данные
- •Дополнение к выводу формул Краскала–Уоллиса
- •Вопросы для самопроверки
- •Лекция 14. Регрессионный анализ
- •Метод наименьших квадратов (мнк)
- •Пример расчета мнк-оценок параметров
- •Оценка тесноты принятой формы связи.
- •Однофакторная линейная зависимость
- •Нелинейные двухпараметрические модели
- •Вопросы для самопроверки
- •Лекция 15. Проблема значимости и адекватности регрессионной модели Оценка значимости регрессионной модели
- •Оценка значимости корреляционной связи
- •Проверка адекватности модели
- •Коэффициент ранговой корреляции Спирмена
- •Вывод формулы для коэффициента ранговой корреляции Спирмена
- •Вопросы для самопроверки
- •Лекция 16. Линейный регрессионный анализ в стандартизованных переменных
- •Способы составления многофакторных моделей
- •Коэффициенты частной корреляции
- •Вывод формул для дисперсий коэффициентов регрессии и расчетных значений
- •Вопросы для самопроверки
Три основных формы интегральной теоремы Лапласа
Для лучшего усвоения материала введем условную классификацию утверждений интегральной теоремы Лапласа и перечислим задачи, которые решаются с помощью каждой из них.
1.
В качестве первой формы теоремы примем
общую формулу для вычисления вероятности
попадания случайной величины в заданные
интервалы:
![]() .
.
2. Вторая форма предназначена для вычисления вероятности попадания случайной величины в интервалы, симметричные относительно центра: Р(|m – a| tm) = 2Ф(t).
Действительно,
для симметричных интервалов m2 = a + tm ,
m1 = a ‑ tm ,
![]() ,
,
![]() .
Вычисляем:
.
Вычисляем:
Р(|m – a| tm) = Р(m1 m m2) = Ф(t) – Ф(–t) = Ф(t) + Ф(t) = 2Ф(t).
В качестве примера применения выведенной формулы ответим на вопросы: "Какова вероятность того, что отклонения случайной величины m от центра a = np не превысят m , 2m , 3m ?
Используя таблицы интегральной функции Лапласа, получим:
Р(|m – a| m) = 2Ф(1) = 20,3413 = 0,6826; Р(|m ‑ a| 2m) = 2Ф(2) = 20,4772 = 0,9544; Р(|m ‑ a| 3m) = 2Ф(3) = 20,4987 = 0,9974.
Только в 3-х случаях из 1000 возможны появления отклонений, превышающие три сигмы; с гарантией 95% можно утверждать, что для распределения Лапласа (и нормального закона Гаусса) случайные отклонения не превысят две сигмы (это утверждение может быть ошибочным лишь в 5-и случаях из 100).
3. Запишем
неравенство |m – a| tm
в эквивалентном виде
![]() и далее (разделив обе части неравенства
на n):
и далее (разделив обе части неравенства
на n):
![]() .
.
Получаем
следующее выражение, которое мы назовем
"Третьей формой интегральной теоремы
Лапласа":
![]() или же
или же
![]() .
В описании этой формулы два раза
встречается слово вероятность Р
и р,
что приводит к неприятным словосочетаниям
типа: "Вероятность того, что относительная
частота
.
В описании этой формулы два раза
встречается слово вероятность Р
и р,
что приводит к неприятным словосочетаниям
типа: "Вероятность того, что относительная
частота
![]() отклонится от вероятности р
появления события в одном испытании не
более чем на ,
равна удвоенному значению функции
Лапласа с аргументом
отклонится от вероятности р
появления события в одном испытании не
более чем на ,
равна удвоенному значению функции
Лапласа с аргументом
![]() ".
Громоздко и малопонятно. Желательно
избегать в одном предложении двух
одинаковых слов, да еще с разным смыслом;
для этого в любом языке есть синонимы.
Например, вероятность некоторого
утверждения
".
Громоздко и малопонятно. Желательно
избегать в одном предложении двух
одинаковых слов, да еще с разным смыслом;
для этого в любом языке есть синонимы.
Например, вероятность некоторого
утверждения
![]() можно назвать "гарантией",
"надежностью", "уровнем доверия".
Кстати, вероятность противоположного
утверждения называют "уровнем
значимости" и обычно обозначают
греческой буквой альфа: = 1 – Р.
Если потребуется, то вероятность р
появления события в одном испытании
можно назвать "долей в совокупности",
а относительную частоту – просто долей.
Выражение
можно назвать "гарантией",
"надежностью", "уровнем доверия".
Кстати, вероятность противоположного
утверждения называют "уровнем
значимости" и обычно обозначают
греческой буквой альфа: = 1 – Р.
Если потребуется, то вероятность р
появления события в одном испытании
можно назвать "долей в совокупности",
а относительную частоту – просто долей.
Выражение
![]() называется "погрешностью". Теперь
теорему можно сформулировать так: "С
уровнем доверия P = 2Ф(t)
можно утверждать, что отклонение
относительной частоты
от своей доли в совокупности р
(от своего предельного значения р)
не превысит погрешности
называется "погрешностью". Теперь
теорему можно сформулировать так: "С
уровнем доверия P = 2Ф(t)
можно утверждать, что отклонение
относительной частоты
от своей доли в совокупности р
(от своего предельного значения р)
не превысит погрешности
![]() .
.
Формула или связывает вместе четыре величины n, p, , P. Если в условиях задачи заданы любые три величины, то четвертую можно найти по вышеприведенной формуле. В связи с этим появляется 4 типа задач.
I. Дано n, p, . Требуется найти Р.
Заданы
параметры распределения n,
p.
Дополнительно задана допустимая
погрешность .
Требуется найти гарантию утверждения
![]() ,
как часто оно будет выполняться.
,
как часто оно будет выполняться.
Решение: Из выражения для погрешности находим t и вычисляем уровень доверия (гарантию) P = 2Ф(t).
Пример. В процессе статистических испытаний монета (р = 0,5) будет подброшена n = 100 раз. Можно ли утверждать, что в результате опыта отклонение относительной частоты от своего теоретического значения (погрешность ) не превысит 0,01?
Найдем
уровень доверия утверждения
![]() .
Из выражения
.
Из выражения
![]() вычисляем t = 0,2
и далее по таблицам Лапласа находим
P = 2Ф(0,2) = 20,079 = 0,158.
Уровень доверия 15,8% не достаточен, чтобы
гарантировать выполнение заданного
условия; т.к. только в 16 случаях из 100
возможны столь отклонения ( = 0,01).
вычисляем t = 0,2
и далее по таблицам Лапласа находим
P = 2Ф(0,2) = 20,079 = 0,158.
Уровень доверия 15,8% не достаточен, чтобы
гарантировать выполнение заданного
условия; т.к. только в 16 случаях из 100
возможны столь отклонения ( = 0,01).
II. Дано n, p, Р. Требуется найти .
Наши утверждения должны быть надежными со стандартным уровнем доверия 90% , 95% , или 99% . Какую предельную погрешность мы можем ожидать с таким заданным уровнем доверия?
Решение: Из соотношения P = 2Ф(t) при заданном Р по таблицам интегральной функции Лапласа находим t. Далее вычисляем предельную ожидаемую погрешность
.
Пример. Предполагается подбросить монету 100 раз. Какую погрешность следует ожидать с гарантией 95% ?
Из
выражения 0,95 = 2Ф(t)
с помощью таблиц Лапласа находим
t = 1,96 2.
Далее вычисляем
![]() .
Иными словами, относительная частота
при 100 испытаниях может варьировать в
довольно широких пределах от 0,4 до 0,6.
.
Иными словами, относительная частота
при 100 испытаниях может варьировать в
довольно широких пределах от 0,4 до 0,6.
III. Дано, p, , Р. Требуется найти n.
Погрешность уменьшается с увеличением числа испытаний. Сколько же требуется провести испытаний, чтобы получать надежные и точные прогнозы?
Решение:
Из соотношения P = 2Ф(t)
при заданном Р
находим t.
Далее записываем условие для предельной
погрешности
![]() ,
откуда при известных p,
,
t находим
n:
,
откуда при известных p,
,
t находим
n:
![]() .
.
Пример. Сколько раз надо подкинуть монету, чтобы с гарантией 90% снизить погрешность до 0,05? Иными словами, сколько требуется испытаний, чтобы с гарантией 90% относительная частота появления герба при бросании монеты не выходила за пределы интервала (0,45; 0,55)?
Из
соотношения 0,9 = 2Ф(t)
находим t = 1,64.
далее из неравенства
![]() определяем
определяем
![]() .
.
IV. Дано n, P и m/n . Найти р.
В предыдущих задачах были заданы параметры распределения и требовалось предсказать результат опыта (задача теории вероятностей). В задаче IV известен результат опыта, и надо сделать заключение о параметрах распределения (именно в этом и заключается статистический способ определения вероятности).
Решение:
Соотношение P = 2Ф(t)
при заданном Р
определяет t.
Далее записываем условие | m/n – p | ,
которое должно выполняться с заданным
уровнем доверия Р:
![]() .
Из этого неравенства находим р.
.
Из этого неравенства находим р.
Пример. В результате 400 бросков монеты относительная частота появления герба получилась равной 0,5. Какие значения параметра р согласуются с такими результатами опыта? Заключение должно иметь 90%‑й уровень доверия.
Из
соотношения 0,9 = 2Ф(t)
находим t = 1,64.
Далее выписываем неравенство
![]() ,
возводим его в квадрат и преобразуем:
(0,5 – р)2 0,0822р(1 – р);
1,0067р2 – 1,0067р + 0,25 0;
отсюда р1 р р2 ,
где р1 , р2
– корни квадратного трехчлена:
р1,2 = 0,5 0,041.
Итак, по результатам опыта можно сделать
заключение, что с гарантией 90% искомая
вероятность р
не выйдет за пределы интервала
0,46 р 0,54.
,
возводим его в квадрат и преобразуем:
(0,5 – р)2 0,0822р(1 – р);
1,0067р2 – 1,0067р + 0,25 0;
отсюда р1 р р2 ,
где р1 , р2
– корни квадратного трехчлена:
р1,2 = 0,5 0,041.
Итак, по результатам опыта можно сделать
заключение, что с гарантией 90% искомая
вероятность р
не выйдет за пределы интервала
0,46 р 0,54.
В заключение темы "Интегральная теорема
Лапласа" заметим, что основная
асимптотическая формула
дает достаточно точные значения лишь
для больших n > 100.
Причина этого – в слишком неточной
замене интегральной суммы интегралом
заключение темы "Интегральная теорема
Лапласа" заметим, что основная
асимптотическая формула
дает достаточно точные значения лишь
для больших n > 100.
Причина этого – в слишком неточной
замене интегральной суммы интегралом
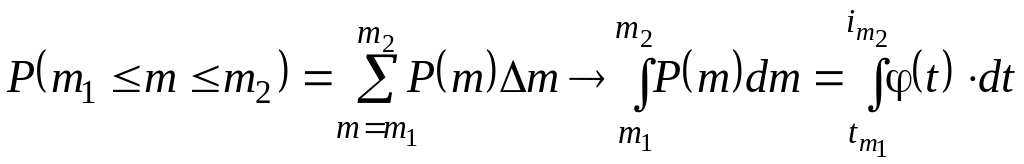 с теми же самыми пределами интегрирования.
На рис. 5.4 изображен полигон распределения
Лапласа для n = 10,
p = 0,3
(локальная формула Лапласа является
достаточно точной аппроксимацией
распределения Бернулли даже для небольших
значений n).
Пусть требуется вычислить
Р(2 m 6) =P(2) + P(3) + P(4) + P(5) +
+ P(6) = P(m).
Так как m = 1,
то Р(2 m 6) = P(m)m.
Это – площадь столбиковой фигуры
(см. рис. 5.4) с границами (m1 – 0,5)
и (m2 + 0,5),
поэтому более правильным будет замена
интегральной суммы интегралом, пределы
которого несколько шире, чем в общепринятой
формуле:
с теми же самыми пределами интегрирования.
На рис. 5.4 изображен полигон распределения
Лапласа для n = 10,
p = 0,3
(локальная формула Лапласа является
достаточно точной аппроксимацией
распределения Бернулли даже для небольших
значений n).
Пусть требуется вычислить
Р(2 m 6) =P(2) + P(3) + P(4) + P(5) +
+ P(6) = P(m).
Так как m = 1,
то Р(2 m 6) = P(m)m.
Это – площадь столбиковой фигуры
(см. рис. 5.4) с границами (m1 – 0,5)
и (m2 + 0,5),
поэтому более правильным будет замена
интегральной суммы интегралом, пределы
которого несколько шире, чем в общепринятой
формуле:
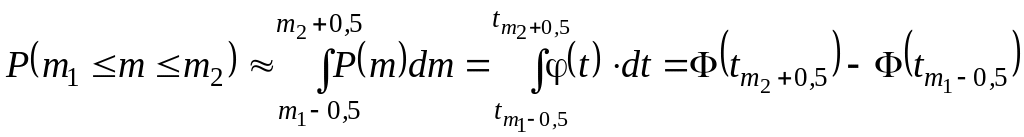 .
.
Так, для нашего примера n = 10, p = 0,3 точное значение Р(2 m 6), рассчитанное по формулам Бернулли, равно P(m) = 0,840; по стандартной формуле Лапласа – Ф(t6) – Ф(t2) = 0,736 (погрешность 12,4%); по уточненной формуле – Ф(t6,5) – Ф(t1,5) = 0,842 (погрешность всего 0,2%).
