Функции случайного аргумента

Рассмотрим закон распределения и характеристики функции Y = (X) случайного аргумента X. Распределение X считается известным.

Если X – дискретная величина, заданная своим рядом распределения, то ряд распределения функции составляется просто заменой x_i на y_i = (x_i):

X

х1

х2

х3

…

хk

Y

(х1)

(х2)

(х3)

…

(хk)

Вер.

p1

p2

p3

…

pk

Вер.

p1

p2

p3

…

pk

Осталось расположить значения y_i в порядке возрастания; вероятности повторяющихся значений y_i надо складывать.

Пример. Дан ряд распределения X. Составим ряд распределения Y = X².

X	–1	0	1	2			Y	1	0	1	4			Y	0	1	4
р	0,2	0,5	0,2	0,1			р	0,2	0,5	0,2	0,1			q	0,5	0,4	0,1

С вычислением характеристик функции нет никаких проблем, причем можно даже не составлять ряд распределения Y:

М(у) = (x_i)p_i .

Для вышеприведенного примера можно найти математическое ожидание функции, предварительно составив ее ряд распределения:

М(у) = y_j q_j = 00,5 + 10,4 + 40,1 = 0,8;

или же непосредственно по исходному ряду для аргумента X:

М(у) = (x_i)² p_i = (–1)²0,2 + 0²0,5 + 1²0,2 + 2²0,1 = 0,8.

Дисперсия функции и моменты 3-го и 4-го порядков вычисляются по обычным формулам: D(y) = M(y²) – (М(у))² , m₃(y) = M(y³), m₄(y) = M(y⁴).

Пусть теперь X – непрерывная величина, заданная функцией плотности вероятности f_x(x). Как и для дискретного случая, характеристики функции Y = (X) можно вычислять непосредственно, не составляя функций распределения для Y:

.

Однако, иногда требуется, зная распределение X, получить в явном виде функции распределения для Y. Обычно нам известна функция плотности вероятности f_x(x) аргумента X. Какой вид имеет функция плотности вероятности f_у(у) для Y = (X) ?

Здесь нам понадобится также функция обратного преобразования X = (Y), которая всегда существует для монотонной ветви преобразования Y = (X). Известно, что или .

Запишем двумя способами формулу для вероятности попадания случайной величины в дифференциально малую окрестность:

.

Отсюда получаем .

Пример. Логнормальное распределение.

Случайная величина распределена по логарифмически нормальному закону, если ее логарифм y = ln x расределен номально. Основна область применеия логнормального закону – социологические и экономические исследованиня. В частности, этим законом хорошо описывается распределение таких экономических показателей, как доход, заработная плата, потребительский спрос и т.п. Логнормальное распределение внешне очень похоже на гамма-распределение и, как гамма-распределение, используется для описания сущестенно положительных величин х > 0.

Если случайная величина y = ln x распределена нормально с характе­ристиками ₀ = М(у) и ₀² = D(x), то этот факт кратко обозначается, как у ~ N(₀; ₀). При этом величина х имеет логнормальное распределение с этими же параметрами, что кратко обозначается как x ~ (₀; ₀). Требование положительности х > 0 можно заменить на более общее условие х > ₀ и рассматривать логнормальное распределение разностей (х – ₀): y = ln (х ‑ ₀). Такое обобщенное логнормальное распределение обозначается (₀; ₀; ₀) и используется в случаях, когда известно, что случайная величина х по своему смыслу не может быть меньше некоторого граничного значения ₀ .

Функцию плотности вероятности (дифференциальную функцию) логнормального распределения получим из следующих соображений. Пусть f_у(y) – дифференциальная функция нормального закона для y = ln (х – ₀):

.

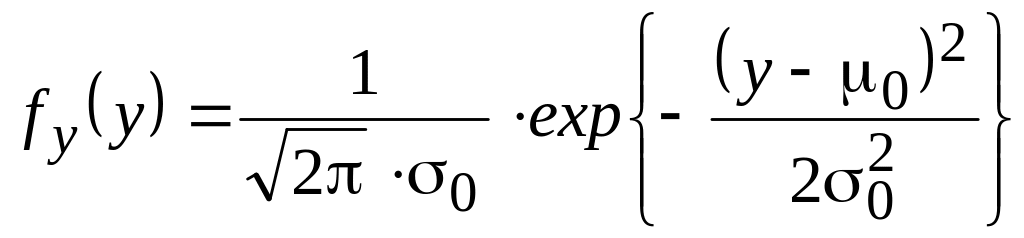Тогда есть вероятность попада­ния случайной величины у в интервал (y, y + dy), или величины х в интервал (х, х + dх). Отсюда получаем функцию плотности вероятности логнормального закона в виде:

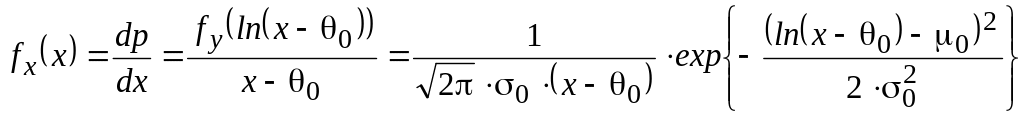
Графики этой функции для разних значений параметров ₀ , ₀ , (₀ =0) приведены на рис. 7.2.

Рис. 7.2. Графики дифференциальной функции логнормального распределения 1 – (₀ =3; ₀ =0,8), 2 – (₀ =3,5; ₀ =0,8), 3 – (₀ =4,5; ₀ =0,8), 4 – (₀ =4,5; ₀ =0,5)

Характеристики ₀ = М(у), ₀² = D(y) связаны с аналогичными характеристиками исходного показателя _х = М(х), _х² = D(х) следующими соотношениями:

, или, наоборот, .