Распределение рабочих по выработке деталей

Выработка деталей за смену одним рабочим, шт.	Число рабочих (веса)	х∙f
18	2	36
19	4	76
20	5	100
21	3	63
22	1	22
Итого:	15	297

По формуле средняя арифметическая взвешенная, шт.:

36 + 76 + 100 + 63 + 22 297

ар.вз.= 15 ⁼ 15 =19,8 ≈20.

Очень часто приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности средним, т.е. среднюю из средних. Например, средняя продолжительность жизни граждан страны представляет собой среднее из средних продолжительностей жизни по отдельным регионам данной страны.

Средние из средних рассчитываются так же, как и сред­не из первоначальных значений признака. При этом средние, которые служат для исчисления на их основе общей средней, принимаются в качестве вариантов.

Вычисление средней арифметической взвешенной из групповых средних осуществляется по формуле:

ар.= ∑ гр.∙ f

∑ f

где f – число единиц в каждой группе.

Результаты вычисления средней арифметической из групповых средних представлены в табл.

Таблица №

Распределение рабочих среднему стажу работы

Номер цеха	Средний стаж работы, лет гр.	Число рабочих, чел. F
1	5	90
2	7	60
3	10	50
Итого:	-	200

В этом примере вариантами являются не индивидуальные данные о стаже работы отдельных рабочих, а средние по каждому цеху гр. Весами f являются численности рабочих в цехах.

Отсюда средний стаж работы рабочих по всему предприятию составит, лет:

ар.= ∑ гр.∙ f = 5∙90+7∙60+10∙50 = 6,85

∑ f 200

Расчет средней арифметической в рядах распределения

Если значения осредняемого признака заданы в виде интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих ин­тервалов, в результате чего образуется дискретный ряд.

Рассмотрим следующий пример.

Группы рабочих по стажу работы (лет), х	Число рабочих, чел., f	Середина интервала, лет х′	х′∙ f
до 5	2	2,5	5
5-10	6	7,5	45
10-15	15	12,5	187,5
15 и более	7	17,5	122,5
Итого	30	-	360

От интервального ряда перейдем к дискретному путем замены интервальных значений их средними значениями (простая средняя между верхней и нижней границами каждого интервала). При этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примы­кающим к ним (второй и предпоследний).

х′₁=0+5 =2,5 х′₂= 5+10 =7,5 х′₃=10+15 = 12,5 х′₄=15+20 = 17,5

2 2 2 2

При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерно­сти распределения единиц признака внутри группы. Однако ошибка будет тем меньше, чем уже интервал и чем больше единиц в интервале.

После того как найдены середины интервалов, вычисле­ния делают также, как и в дискретном ряду, - варианты ум­ножают на частоты (веса) и сумму произведений делят на сум­му частот (весов), тыс. руб.:

ар.= ∑x′∙f

∑f

Итак, средний стаж работы составляет 12 лет.

Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчета средней можно упростить и облегчить, если воспользоваться ее свойствами. Приведем (без доказательства) некоторые основные свойства средней арифметической.

Свойство 1. Если вес индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака соответственно уменьшится или увели­чится в i раз.

Свойство 2. Если все варианты осредняемого признака уменьшить или увеличить на число А , то средняя арифметиче­ская соответственно уменьшится или увеличится на это же число А.

Свойство 3. Если веса всех осредняемых вариантов уменьшить или увеличить в k раз, то средняя арифметическая не изменится.

Средняя гармоническая.

Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной.

Необходимо подчеркнуть, при расчете средних показателей помимо средней арифметической могут использоваться и другие виды сред­них, но любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть определяющий показатель, который связан с осредняемым показателем (например, при замене фактических заработных плат отдельных работников предприятия средней заработной платой, не должен изме­ниться фонд заработной платы). В каждом конкретном случае в зависимости от характера имеющихся данных, сущности изучаемого социально-экономического явления.

Вид средней определяется характером взаимосвязи опре­деляющего показателя с осредняемым.

Так, например, средняя арифметическая при­меняется в тех случаях, когда известны варианты варьирующего признака х и их частоты.

Если статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение х∙f, применяется формула средней гармо­нической взвешенной. Чтобы исчислить среднюю, обозначим х∙f =w, откуда f = w/x . Теперь преобразуем формулу сред­ней арифметической таким образом, чтобы по имеющимся данным х и w можно было исчислить среднюю. В формулу средней арифметической взвешенной вместо х∙f, подставим w, вместо f – отношение w/x и получим формулу средней гармонической взвешенной

гар.= ∑ w = w1+w2+w3....wn

∑w w1+w2+w3...wn

x x1 x2 x3 x n

Формула показывает, что средняя гармоническая - средняя взвешенная из варьирующих обратных значений при­знака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда мож­но рассчитать среднюю арифметическую. Итак, средняя гармоническая применяется то­гда, когда неизвестны действительные веса f, а известно w = х ∙ f, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины: 1 1 1

х1, х₂ х3

Например, по данным, приведенным в таблице требуется определить среднюю цену 1 кг картофеля.

Таблица №

Цена и выручка от реализации по трем коммерческим магазинам в сентябре 1994 года

Номер магазина	Цена картофеля, руб./кг, х	Выручка от реализации, млн. руб. W	количество реализованных единиц. кг f=w/x
1.	900	18	20000
2.	1000	15	15000
3.	800	24	30000
		57	65000

Расчет средней цены выражается соотношением:

Выручка от реализации, руб.

Средняя цена, руб. = количество реализованных единиц, кг

Определяющий показатель в данном случае - числитель этой логической формулы. Выручка от реализации w известна (числитель), а количество реализованных единиц - неизвестно, но может быть найдено как частное от деления одного показа­теля на другой, для чего нужно отдельно по каждому магазину разделить выручку на цену.

Тогда средняя цена 1 кг картофеля, руб., по трем ком­мерческим магазинам может быть исчислена по формуле средней гармонической взвешенной:

гар.= ∑ w = 18000000+15000000+24000000 57000000 = 876,92 руб.

∑w 18000000+15000000+24000000 = 65000

x 900 1000 800

Этот же результат получится и по средней арифметической взвешенной, если в качестве весов принять количество проданных единиц (которые необходимо предварительно рас­считать), руб.:

гар.= 800∙30 000+ 1000∙15 000 + 900∙20 000 ₌ 57000000 ₌ 876,92 руб.

30000 + 15000 + 20000 65000

Полученная средняя цена 1 кг картофеля является реаль­ной величиной, ее произведение на все количество проданного картофеля дает общий объем реализации, выступающий в качестве определяющего показателя (57 млн руб). Исчисление средней гармонической взвешенной по формуле освобождает от необходимости предварительного расчета весов, поскольку эта операция заложена в саму формулу. В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, ис­числяемая по формуле:

гар.=1+1+...+1 = __n

1 + 1 + 1 ∑ 1

x1 x2 xn x

1

где x — отдельные варианты обратного признака, встречающиеся по одному разу; n — число вариантов.

Пример . Цена за единицу товара А, продаваемого в пер­вой торговой точке, составила 20 руб., во второй - 30 руб. Какова средняя продажная цена товара, если выручка от продаж товара в торговых точках одинакова?

Решение

Поскольку весами при расчете средней являются выручки от продажи (товарообороты), а сама выручка представляет собой произведение цены x на количество проданного товара f, вычис­ления проводили по средней гармонической взвешенной. Равен­ство весов позволяет осуществлять расчеты по формуле средней гармонической простой:

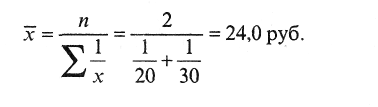
Средняя геометрическая

Среднюю геометрическую применяют случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическая исчисляется - извлечением корня степени п из произведений отдельных значений — вариантов признака х:

где п — число вариантов; П - знак произведения.

Среднюю геометрическую наиболее часто применяют для определения средних темпов изменения в рядах динамики, а также в рядах распределения. I

Средняя квадратическая и средняя кубическая

В экономической практике иногда необходимо делать расчет среднего размера признака, выражен­ного в квадратных или кубических единицах измерения. В этих случаях применяется средняя квадратическая (например, для вычисления средней величины стороны п квадратных участ­ков, средних диаметров труб, стволов и т.п.) и средняя куби­ческая (например, при определении средней длины стороны п кубов).

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

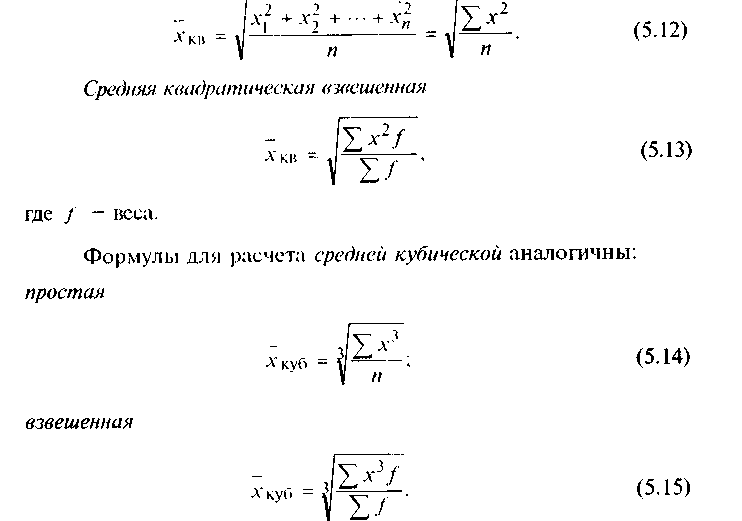
Средние квадратическая и кубическая имеют ограничен­ное применение в практике статистики.

Структурные средние

Мода.

Характеристиками вариационных рядов, наряду со средними, являются мода и медиана.

Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.

Пример

Распределение проданной обуви по размерам характеризуется следующими При изучении вариации применяются такие характеристики вариационного ряда, которые описывают количественно его структуру, строение. Такова, например, медиана - величина варьирующего признака, которое находится в середине вариационного ряда и делит совокупность на две равные части. Чтобы найти медиану необходимо найти значение признака, которое находится в середине упорядоченного ряда (медианой является собственный капитал третьего банка из пяти в табл. 5.5, т.е. 196 млрд руб.).

показателями:

Размер обуви	36	37	38	39	40	41	42	43	44	45
Число проданных пар	-	1	6	8	22	30	20	11	1	1

В этом ряду распределения мода равна 41. Именно этот размер обуви пользуется наибольшим спросом у покупателей.

В интервальном вариационном ряду модой приближенно считается центральный вариант так называемого модального интервала т.е. того интервала, который имеет наибольшую частоту. В пределах интервала можно найти то значение признака, которое является модой.

Для интервальных рядов распределения с равными интервалами мода определяется по формуле:

где - начальное значение интервала, содержащего моду;

- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным.

Мода применяется в статистической практике при изучении покупательного спроса, регистрации цен и т.д.

Медиана распределения

Таблица 5.5

Крупные банки Санкт-Петербурга, ранжированные по размерам

собственного капитала

Название банка	Собственный капитал, млрд. руб.
Петроагропромбанк	71
Петровский	146
Балтийский	196
Альфа	201
Промстройбанк	731

На примере табл. 5.5 видно принципиальное различие между медианой и средней величиной. Медиана не зависит от значений признака на краях ранжированного ряда. Если бы даже капитал крупнейшего банка Санкт-Петербурга был вдесятеро больше, величина медианы не изменилась бы. Поэтому часто медиану используют как более надежный показатель типичного значения признака, нежели арифметическая средняя, если ряд значений неоднороден, включает резкие отклонения от средней. В данном ряду средняя величина собственного капитала, равная 269 млрд руб., сложилась под большим влиянием наибольшей варианты. 80% банков имеют капитал меньше среднего и лишь 20% - больше. Вряд ли такую среднюю можно считать типичной величиной. При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при десяти значениях признака - среднюю из пятого и шестого значений в ранжированном ряду. Номер медианы для нечетного числа совокупности вычисляется по формуле

N=(n+1) \ 2

В интервальном вариационном ряду для нахождения медианы применяется формула (5.14).

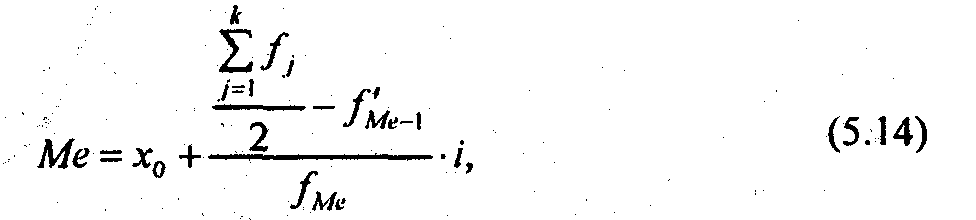
где Me - медиана;

х₀ - нижняя граница интервала, в котором находится медиана;

f^’ _Mе-1 - накопленная частота в интервале, предшествующем медианному;

f_Me - частота в медианном интервале;

i - величина интервала;

k - число групп.

В дискретном вариационном ряду медианой следует считать значение признака в той группе, в которой накопленная частота; превышает половину численности совокупности.

Пример

Распределение предприятий по численности промышленно-производственного персонала характеризуется следующими данными:

Группы предприятий по числу работающих	Число предприятий	Накопленная частота
100-200	1	1
200-300	3	4
300-400	30	34
400-500	7	41
500-600	19	60
600-700	15	75
700-800	5	80
Итого:	80	-

Определите среднюю численность предприятий, моду и медиану.

В этой задаче наибольшее число предприятий (30) имеет численность работающих от 300 до 400. Следовательно, этот интервал является модальным интервалом ряда распределения.

Мо= 300+100∙ 30-3_______ = 354чел.

(30-3)+(30-7)

Следовательно, наиболее часто встречаются предприятия со средней численностью 354 человека.

Ме = 400+100∙40-34 = 486

7

Следовательно, половина предприятий имеет численность работающих меньше 486 человек, а другая половина имеет численность больше данного показателя.

ар.вз. =150∙1+250∙3+350∙30+450∙7+550∙19+650∙15+750∙5 =481,25

80

Средняя численность работающих составляет 481,25 человек.