Конспект заняття математичного гуртка. 9-й клас

Тема. Теореми Чеви і Менелая

Мета: Формувати вміння застосовувати теореми Чеви і Менелая до розв'язування задач.

Завдання:

1. сформулювати і довести теореми Чеви і Менедая;

2. показати їх застосування до доведення відомих і доведених раніше тверджень;

3. вчити використовувати ці теореми під час розв'язування задач на доведення і обчислення.

Підготовка до заняття. Напередодні засідання учитель дає завдання трьом учням підготувати доведення тверджень про перетин в одній точці бісектрис внутрішніх кутів трикутника, висот і медіан трикутника, поділ кожної медіани їх точкою перетину на частини, відношення довжин яких дорівнює 2:1, якщо вимірювати довжину першої частини від вершини. Четвертий учень готує повідомлення про Чеву Джованні та Менелая Александрійського.

Хід заняття

І. Мотивація. Учні відтворюють на дошці доведення вище перелічених тверджень.

1-й учень

Д ано: ΔАВС, АL₁,ВL₂,СL₃ – бісектриси.

Довести: АL₁∩ВL₂∩СL₃ = I.

Доведення. АL₁∩ВL₂ = I (за теоремою про пряму, що не проходить через жодну з вершин трикутника і перетинає одну з його сторін. Розглянути ΔВL₂С і пряму АL₁).

ІК АС, ІМ АВ, ІN BC. IK=IM=IN (за властивістю точок бісектриси кута).

Оскільки точка І рівновіддалена від сторін АСВ, то І СL₃. Отже, АL₁∩ВL₂∩СL₃ = I.

2-й учень

Дано: ΔАВС, АН₁,ВН₂,СН₃ – висоти.

Д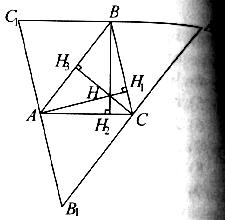 овести: АН₁∩ВН₂∩СН₃ = Н.

Доведення. Проведемо через вершини ΔАВС прямі паралельні протилежним сторонам:

В С₁А₁, С₁А₁||АС; С В₁А₁, В₁А₁||АВ; А В₁С₁, В₁С₁||СВ.

Для ΔА₁В₁С₁ висоти ΔАВС є серединними перпендикулярами, що перетинаються, як відомо, в одній точці.

Отже, АН₁∩ВН₂∩СН₃ = Н.

3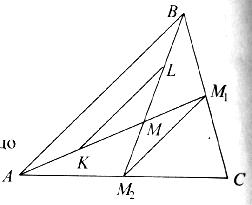 -й учень

Дано: ΔАВС, АМ₁,ВМ₂,СМ₃ – медіани.

Довести: АМ₁∩ВМ₂∩СМ₃ = М,

АМ:ММ₁ = ВМ:ММ₂ = СМ:ММ₃ =2:1.

Доведення. АМ₁∩ВМ₂ = М (за теоремою про пряму, що не проходить через жодну з вершин трикутника і перетинає одну з його сторін. Розглянути ΔВМ₂С і пряму АМ₁). К АМ, АК = КМ; L ВМ, ВL = LМ.

Чотирикутник КLМ₁М₂ – паралелограм (ознака за двома протилежними сторонами). Тоді КМ = ММ₁. Оскільки КМ = АМ, то ММ₁ = АМ. Отже, АМ:ММ₁ = 2:1.

Аналогічно доводиться рівність ВМ: ММ₂ =2:1.

Припустимо, що М СМ₃ і, нехай СМ₃∩АМ₁ = М', М' відмінна від М. Тоді АМ':М'M₁ =2:1, чого бути не може. Отже, точки М і М' збігаються.

Рівність СМ:ММ₃ =2:1 доводиться аналогічно доведенню попередніх рівностей.

Учитель звертає увагу учнів на різноманітність доведень і підводить до запитання: «Чи можна довести перетин бісектрис, висот і медіан трикутника використовуючи одну спільну ідею доведення?»

II. Формулювання і доведення теореми Чеви.

Учитель повідомляє учням, що довести попередні твердження можна, якщо знати наступну теорему.

Теорема Чеви. Прямі, що проходять через вершини ΔАВС і перетинають його сторони АВ, ВС, СА (або їх продовження) відповідно в точках С₁, А₁ і В₁, перетинаються в одній точці тоді і тільки тоді, коли виконується рівність

.

Д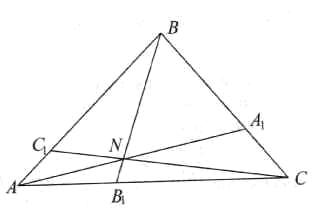 оведення теореми складається з двох частин.

Доведення необхідності

Дано: ΔАВС, АА₁∩ВВ₂∩СС₃ = N.

Довести: .

Доведення. Для доведення використаємо властивість площ трикутників з рівною висотою. .

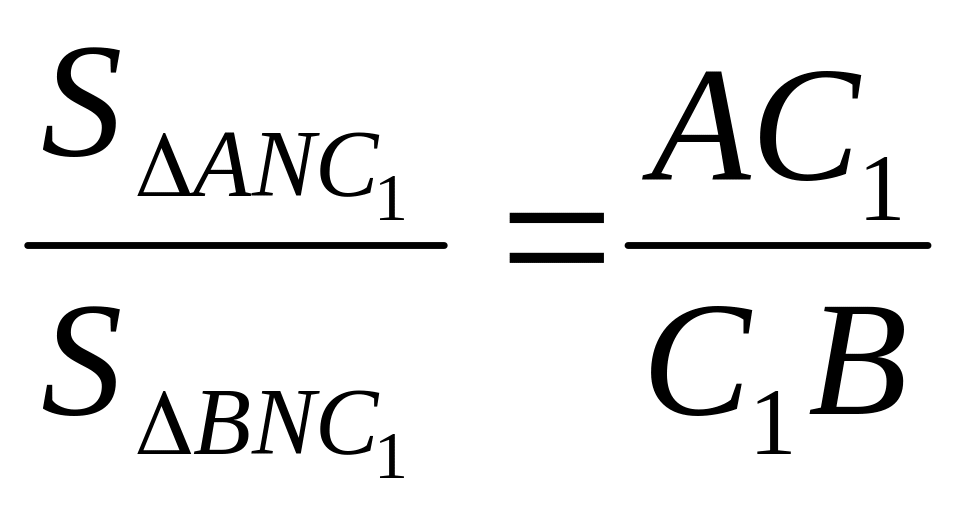Оскільки і , то (1).

Аналогічно, враховуючи, що , , , одержуємо наступні рівності:

(2), (3).

Перемножимо почленно рівності 1-3:

.

Доведення достатності

Дано: ΔАВС, А₁ ВС, В₁ АС, С₁ АВ, .

Довести: АА₁∩ВВ₂∩СС₃ = N.

Доведення. Нехай АА₁∩ВВ₂=N і N СС₁. Проведемо пряму СN, СN АВ=С₁'.

Точка С₁' відмінна від точки С₁. Тоді 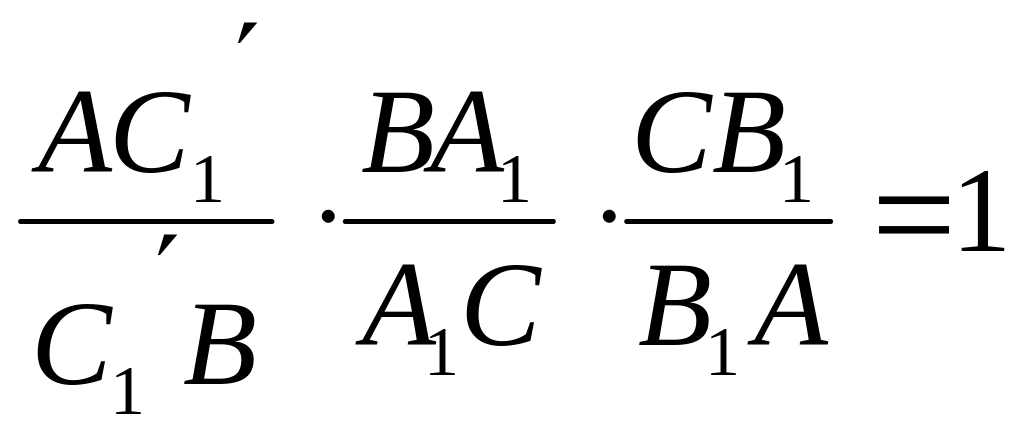(за доведеною необхідністю).

Враховуючи дану в умові рівність, одержуємо 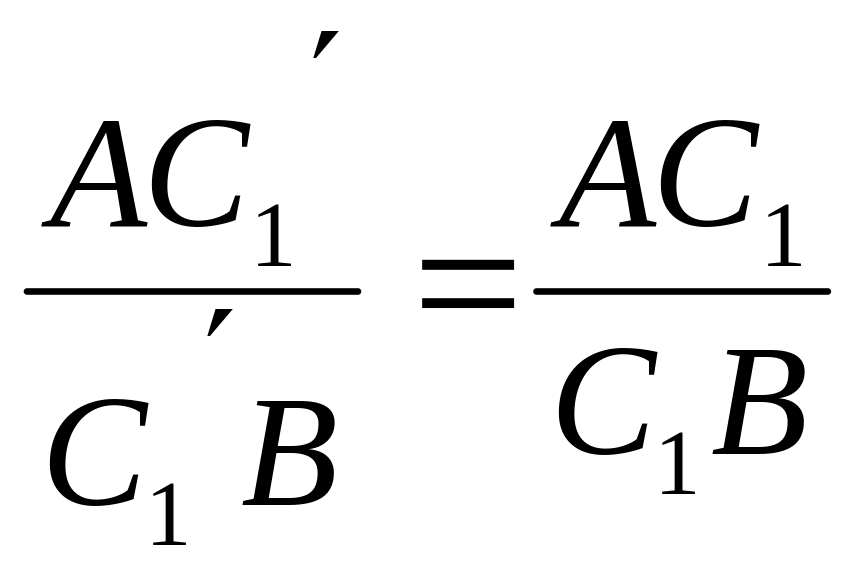, чого бути не може.

Отже, точки С₁ і С₁' збігаються, і N СС₁. Теорему доведено.

Після доведення теореми учень робить повідомлення про її автора. Джованні Чева (1648-1734) - італійський інженер гідравлік і геометр. Народився в Мілані. Створив учення про січні, яке поклало початок новій синтетичній геометрії. Це вчення викладено в роботі «Про прямі, що взаємно перетинаються» (1678). Властивості прямолінійних фігур доведені в цій роботі за допомогою розгляду властивостей центра інерції (ваги) системи точок.

Ш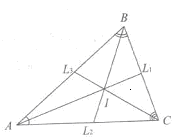 . Доведення перетину бісектрис, висот і медіан трикутника за допомогою теореми Чеви.

Учні самостійно доводять твердження. При потребі вчитель надає консультації. Троє учнів відтворюють відповідні доведення на дошці.

1. За властивістю бісектриси внутрішнього кута трикутника:

, , .

Перемноживши отримані рівності, маємо .

2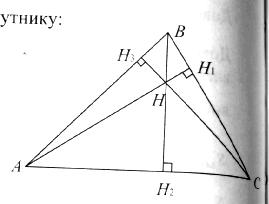 . Згідно співвідношень у прямокутному трикутнику: , .

Тоді .

Аналогічно, і .

Перемноживши отримані рівності, маємо

.

3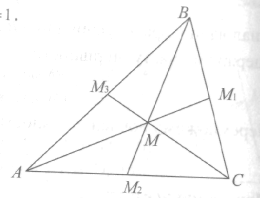 . За означенням медіани:

, , .

Отже, .

Після обговорень доведень перетинів, учитель звертає увагу учнів на те, що теорема Чеви не дає можливості довести властивість точки перетину медіан, і пропонує розглянути ще одну теорему.

IV. Формулювання і доведення теореми Менелая.

Теорема Менелая. Якщо пряма перетинає сторони АС, ВС, АВ трикутника АВС (або їх продовження) в точках В,, А,, С,, то має місце співвідношення .

Д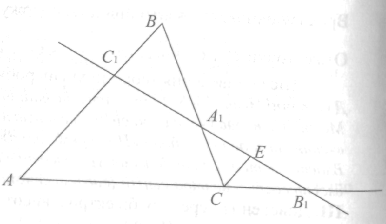 ано: пряма а, а∩АВ=С₁, а∩ВС=А₁, а∩АС=В₁.

Довести: .

Доведення. Проведемо СЕ||АВ.

ΔАВ₁С₁~ΔСВ₁Е. Тоді (1).

Δ С₁ВА₁~Δ ЕСА₁. Тоді (2).

Перемножимо почленно рівності (1) і (2): . Тоді .

Поділимо праву і ліву частини останньої рівності на .

Одержимо , або .

Теорему доведено.

Після доведення теореми учень знову робить повідомлення про її автора.

Менелай Александрійський (1-2 ст. н.е.) — грецький математик і астроном. %цв у Римі. Відомі його роботи в області сферичної тригонометрії Збереглося шість його книг про обчислення хорд і три книги «Сферики». Саме в третій книзі «Сферик» викладено теорему про пряму, що перетинає сторони трикутника, яку пізніше названо теоремою Менелая. За деякими відомостями, Менелай також вивчав криві на поверхні. Згідно арабських джерел, йому належить ще і робота з гідростатики.

Далі учитель разом з учнями доводить властивість точки перетину медіан.

Дано: ΔАВС, АМ₁, ВМ₂, СМ₃, – медіани, АМ₁∩ВМ₂∩СМ₃ = М.

Д овести: АМ:ММ₁ = ВМ:ММ₂ = СМ:ММ₃ = 2:1.

Доведення. Розглянемо ΔАВМ₂ і пряму М₃С.

Згідно теореми Менелая: .

(Під час виписування необхідної рівності, учитель звертає увагу учнів на те, як правильно треба «обходити» вершини трикутника і точки на його сторонах: від вершини до точки – від точки до наступної вершини і т.д.)

Оскільки АМ₃=М₃В і СА=2М₂С, то . Тому .

Далі учні самостійно доводять, що (розглянути ΔСАМ₁ і пряму ВМ₂) і (розглянути ΔСВМ₃ і пряму АМ₁).

V. Застосування теорем Чеви і Менелая до розв'язування задач

Задача 1. У ΔАВС проведено висоту ВН₂, АН₂:Н₂С = 1:2. Ортоцентр Н поділяє цю висоту у відношенні 3:2, починаючи від вершини трикутника. У якому відношенні дві інші висоти поділяють сторони трикутника, до яких вони проведені. Чи можна визначити вид цього трикутника?

Р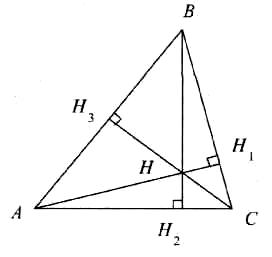 озв'язання

Розглянемо ΔВН₂С і пряму АН₁.

За теоремою Менелая: .

Оскільки , , то .

Тому .

Для ΔАВС за теоремою Чеви

або .