министерство образования и науки Российской федерации

Государственное образовательное учреждение высшего профессионального образования

«национальный исследовательский

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Институт природных ресурсов

Кафедра геофизики

Отчет по лабораторной работе № 3

ОЦЕНКА НАИБОЛЕЕ ВЕРОЯТНЫХ ЗНАЧЕНИЙ ФИЗИЧЕСКИХ СВОЙСТВ

МАССИВОВ ГОРНЫХ ПОРОД ПО КРИТЕРИЯМ СОГЛАСИЯ

В-5

Выполнил: ст. гр. 2270

Проподалина А.

Мишина Д.

Проверил: доцент

Гусев Е.В.

Томск 2012

Цель работы: знакомство со способами статистической обработки данных массовых измерений и получение навыков в применении критериев согласия при обработке геофизических данных.

1.Основные теоретические сведения

При проектировании геофизических работ, оценке эффективности геофизических методов (например, по коэффициенту петрофизической контрастности), а также при интерпретации геофизических данных используют статистические параметры физических свойств, определенные по большому числу измерений на образцах горных пород.

На первом этапе обработка петрофизических данных заключается в вычислении ряда распределения значений измеренного параметра X и построении вариационной кривой (или гистограммы), для чего промежуток значений (Xmax - Xmin) делят на K интервалов по определенному правилу. При вычислении числа интервалов (классов группировки) K может быть использована эмпирическая формулаК = 1 + 4 lgN, где N - общее число значений параметра в выборке (объем выборки).

В этом случае длину интервала группирования определяют по формуле:

,

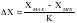Рассчитанное значение  не должно быть менее двойной погрешности измерений параметра.

При больших объемах выборки длину интервала группирования можно определить по формуле Стерджеса:

.

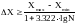В графическом виде ряд распределения может быть представлен, как полигон распределения, или как гистограмма распределения (рис. 1, 2). По вертикальной оси откладывают либо частоты n, либо частости Р. Плавная кривая, соединяющая средние точки ступеней гистограммы, называется вариационной кривой.

При достаточно больших выборках частости (P) ,будут приближаться к вероятностям попадания случайной величины в i-тый интервал (т.е. к плотностям вероятности), а вариационная кривая будет приближаться к закону распределения вероятностей измеренной величины (признака) Х.

Наиболее вероятные статистические характеристики физических свойств для массивов горных пород определяются в зависимости от закона распределения данного признака. Для петрофизических групп пород наиболее распространены два закона распределения - распределение Гаусса (нормальный закон распределения) и логарифмически нормальное распределение (логнормальный закон).

1. Нормальный закон распределения.

Нормальным (или гауссовым) называют распределение вероятностей непрерывной случайной величины, которое описывается функцией:

, (1)

где M - математическое ожидание,  - среднее квадратическое отклонение (стандарт) случайной величины X.

Как это видно из формулы (1), нормальное распределение определяется двумя параметрами - M и . При этом математическое ожидание (М), модальное значение (Mo) и медиана (Me) численно совпадают. В том случае, когда M = 0 и  = 1, нормальную кривую называют нормированной. При вычислении выборочных характеристик по вариационному ряду:

или , (2)

или , (3)

, ,

где D - дисперсия случайной величины, - значения случайной величины в центрах интервалов.

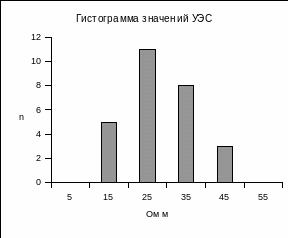
Рис. 1 Рис. 2

2. Логнормальный закон распределения.

Значения случайной величины X считаются распределенными логарифмически нормально, если логарифмы этих значений распределены по нормальному (Гауссовскому) закону. То есть, логарифмически нормальный закон можно считать логарифмически преобразованным нормальным законом, поэтому функция плотности вероятности логарифмов аналогична нормальному закону распределения:

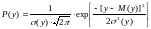, (4)

где 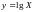, математическое ожидание величины , - стандарт величины (логарифмический стандарт).

Рис. 3 . Логнормальное распределение величины Х в линейном масштабе.

Рис. 4. Логнормальное распределение величины Х в логарифмическом масштабе.

3. Критерий согласия Пирсона.

В математической статистике гипотезу о принадлежности закона распределения к нормальному называют основной (нулевой) гипотезой. Статистическую проверку этой гипотезы по выборке производят при помощи критериев согласия. Такие критерии позволяют определить вероятность того, что при выполнении предполагаемого закона распределения наблюдающиеся в выборке отклонения от этого закона являются случайными, а не свидетельствуют об ошибочности гипотезы. Если такая вероятность велика, то отклонения от предполагаемого закона признаются случайными, а нулевая гипотеза о законе распределения не опровергается.

В исследовательской практике применяются самые различные критерии согласия, которые оформлены в виде государственных стандартов (напр., ГОСТ 11.006-74 “Прикладная статистика.Правила проверки согласия опытного распределения с теоретическим”).

Проверка основной гипотезы с применением критериев согласия необходима чаще всего для обоснования возможности принятия тех или иных статистических решений. Наибольшее применение получили критерии согласия Колмогорова, Пирсона, Смирнова и др. Среди них наиболее общим, применяющимся для проверки не только нормального закона, но и других, является критерий Пирсона или критерий ² (“хи - квадрат”).

В основе метода сравнения по критерию ² лежит сравнение фактически наблюдаемых частот с теоретическими, которые вычисляются в предположении нормального распределения. Как правило, эти частоты отличаются друг от друга.

Теоретические частоты вычисляются с применением функции Лапласа (интеграла вероятности) Ф₀(Z), где Z - нормированная переменная, определяемая по формуле:

Z_i= (X_i -M) /  .

В этой формуле М - математическое ожидание,  - стандартное отклонение. Наименьшее значение Z_i= Z₁ получают равным - , а наибольшее + . Тогда теоретические вероятности попадания в i-тый интервал (теоретические частости) вычисляются по следующей формуле:

. (5)

После того, как полученные значения теоретических вероятностей попадания умножим на объем выборки N, получим значения теоретических частот. Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты. При уровне значимости  требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. Уровень значимости  - это вероятность ошибочно отвергнуть нулевую гипотезу, когда она верна.

В качестве критерия для сравнения теоретических и фактических частот (а тем самым - проверки основной гипотезы) используют случайную величину:

, (6)

где через 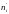обозначены теоретические частоты попадания в интервал, аК - означает число интервалов. Случайной эта величина является вследствие случайности выборки и значений фактических частот . Чем ближе друг к другу фактические и теоретические частоты для каждого интервала, тем меньше величина , а это служит признаком близости фактического и предполагаемого законов распределения.