9.5. Повний диференціал і його застосування

Згідно з означенням функція диференційована в точці , якщо її приріст у цій точці можна подати у вигляді (9.4) з урахуванням (9.5):

,

де – нескінченно малі при .

Означення. Головна, лінійна відносно і , частина приросту диференційованої функції у точці називається її повним диференціалом у цій точці і позначається . Отже за означенням:

. (9.7)

Якщо , то і аналогічно , тобто диференціали незалежних змінних дорівнюють їх приростам. Отже (9.7) можна записати і так:

.

Така форма запису повного диференціала є найбільш уживаною.

Наведене означення без труднощів розповсюджується на функції трьох і більшого числа незалежних змінних. Так, повним диференціалом функції від незалежних змінних ми назвемо вираз

.

Приклади.

1. Знайти повний диференціал функції .

Маємо:

;

.

Отже

.

2. Знайти повний диференціал функції .

2. Обчислити повний приріст і повний диференціал функції

у точці , якщо

а

Маємо

.

.

.

Тоді .

Як бачимо, повний приріст і повний диференціал мало відрізняються один від одного. Це є природнім, тому що прирости аргументів досить малі, а різниця між повним приростом і повним диференціалом є нескінченно малою вищого порядку.

На цьому ґрунтується застосування повного диференціала в наближених обчисленнях. Згідно з формулою (9.5)

,

де – нескінченно малі при .

Нехтуючи нескінченно малі вищого порядку при достатньо малих і , одержимо наближену рівність

,

або ,

звідки

. (9.8)

Формула (9.8) дозволяє легко обчислити наближене значення, якщо відомі значення . Ця формула природним чином розповсюджується на функції трьох і більше незалежних змінних.

Приклад. Обчислити наближено за допомогою повного диференціала

.

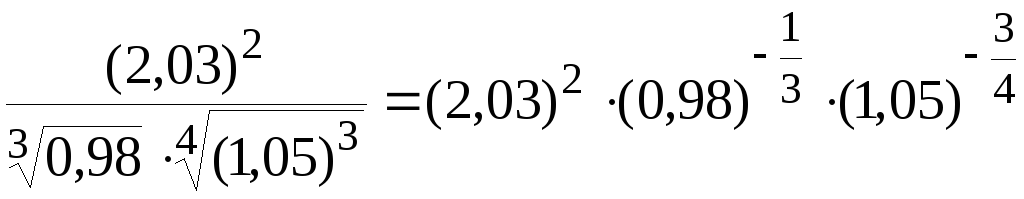Шукане число розглядатимемо як значення функції

в точці (2,03; 0,98; 1,05).

Покладемо .

Тоді

.

Підставляємо числові значення:

.

Безпосереднє обчислення з точністю до четвертого знака дає значення 3,9997 (відносна похибка менша, ніж 0,1%).

Повний диференціал застосовується також при оцінках похибок. Нехай обчислювана величина , де наближені значення відомі з граничними абсолютними похибками відповідно . Тоді за наближене значення величини природно взяти .

Для підрахунку граничної абсолютної похибки зазначимо, що насправді

,

де звідки, якщо малі, а значить і малі, маємо

отже

Таким чином отримуємо оцінку граничної абсолютної похибки величини :

. (9.9)

Щоб оцінити граничну відносну похибку величини , поділимо обидві частини рівності (9.9) на :

, (9.10)

що можна записати (перевірте) як , тобто гранична відносна похибка величини дорівнює граничній абсолютній похибці її натурального логарифма. Зазначимо, що формула (9.9) узагальнює формулу (7.19) із п. 7.7, виведену для функції однієї змінної.

Приклад. Резервуар має форму правильної зрізаної чотирикутної піраміди (рис. 9.8). Вимірювання його розмірів дало такі результати:

• сторона нижньої основи м;

• сторона верхньої основи м;

• висота м.

Р И С 9.8 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Потрібно обчислити наближене значення об’єму резервуара та його абсолютну і відносну граничні похибки.

Об’єм зрізаної піраміди обчислюється за формулою

,

отже його наближене значення

.

Гранична абсолютна похибка за формулою (9.9) дорівнює

.

Таким чином .

Гранична відносна похибка дорівнює

.