9.8. Скалярне поле. Градієнт і похідна за напрямом.

Є багато випадків, коли в наукових чи технічних дослідженнях доводиться розглядати значення тієї чи іншої величини в кожній точці даної частини простору. Якщо кожній точці даної частини простору відповідає повне значення величини , то кажуть, що у цій частині простору задано поле цієї величини. Якщо поле змінюється з часом, то його називають нестаціонарним, а поле, яке не залежить від часу, називається стаціонарним. Ми тут розглядатимемо лише стаціонарні поля.

Якщо число, то поле називається скалярним (наприклад поле температури, тиску, густини), якщо ж векторна величина, то поле називають векторним (наприклад поле швидкостей частиною рідини або газу, поле сили тяжіння, напруженість електричного поля). Розглядаються поля і більш загальної природи (наприклад тензорні). В даному розділі ми обмежимося розглядом лише скалярних полів.

Сформульоване означення скалярного поля проголошує, що кожній точці даної області простору поставлено у відповідність єдине значення скалярної величини . Це означає, що величина задана як функція точки цієї області: . Якщо в просторі запроваджено ту чи іншу систему координат, то між точками простору і наборами їхніх координат встановлено взаємно однозначну відповідність, і тоді поле описується функцією кількох змінних – координат точки , Для тривимірного простору і декартових координат маємо

. (9.17)

При переході від даної точки до іншої скалярне поле (9.17) змінює свою величину. Нас цікавить швидкість цієї зміни при переміщенні в заданому напрямі. Нехай напрям переміщення задано вектором . Візьмемо в цьому напрямі на відстані від точки точку (рис. 9.10). Тоді

.

Р И С 9.10. !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Приріст функції при переході від точки до в напрямі вектора позначимо

.

Відношення є середня швидкість зміни поля в напрямі .

Означення. Якщо існує границя відношення при , то цю границю називають похідною поля в точці за напрямом вектора і позначають

.

Якщо поле диференційоване в точці , то

,

де нескінченно мала вищого порядку, ніж , тобто . Зазначимо, що

де напрямні косинуси вектора . Тоді

.

Переходячи до границі при , одержимо формулу для обчислення похідної за напрямом:

. (9.18)

Частинні похідні є окремими випадками похідної за напрямом. Нехай, наприклад, . Оскільки , то за формулою (9.18) маємо

,

тобто частинна похідна по аргументу є похідна за напрямом осі (її орта ). Аналогічні висновки мають місце і для частинних похідних по решті аргументів.

Із означення похідної за напрямом випливає, що її абсолютна величина дає значення швидкості зміни поля в даному напрямі, а її знак визначає характер зміни поля (зростання чи спадання).

Означення. Вектор, координатами якого є частинні похідні поля в точці , називається градієнтом поля в цій точці і позначається

. (9.19)

Якщо позначимо орт вектора через

,

то формула (9.18) визначить як скалярний добуток

(9.20)

З формули (9.20) випливає, що похідна поля в даній точці за напрямом вектора має найбільше значення, якщо напрям вектора збігається з напрямом градієнта. Справді, в цьому разі , тобто , при чому знак рівності має місце лише тоді, коли .

Таким чином вектор градієнт спрямований в напрямі найшвидшого зростання поля , а його модуль дорівнює найбільшій швидкості зростання поля. Це означає, що є також характеристичною скалярною поля , яка інваріантно притаманна даному полю і не залежить від вибору системи координат. Отже скалярне поле породжує векторне поле , визначене у тій же області.

Приклади.

1. Знайти похідну поля у точці в напрямі радіуса – вектора цієї точки.

Знаходимо напрямні косинуси радіуса – вектора точки :

.

.

Отже

.

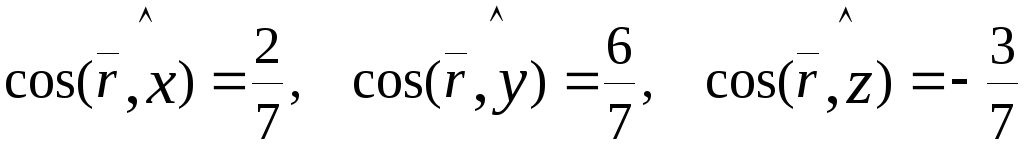За формулою (9.18)

.

2. Обчислити найбільшу крутизну поверхні в точці і вказати її напрям.

Згідно з властивостями градієнта напрямом найшвидшого зростання функції (найбільшої крутизни її графіка) є напрям градієнта цієї функції, а сама ця крутизна (найбільша швидкість зростання) дорівнює модулю градієнта.

Знаходимо:

;

.

Отже

,

Звідки

;

Таким чином найбільша найбільша крутизна поверхні у заданій точці складає , а її напрям утворює з віссю кут .

9.9. Дотична площина і нормаль до поверхні.

З властивостями градієнта пов’язані деякі геометричні застосування диференціального числення функцій кількох змінних.

Означення. Розглянемо поверхню, задану рівнянням

(9.21)

Пряма лінія називається дотичною до поверхні (9.21) в деякій її точці , якщо вона є дотичною до будь – якої кривої, що лежить на поверхні і проходить через точку (рис. 9.11).

Р И С, 9. 11 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Означення. Якщо всі дотичні прямі до поверхні (9.21) в точці лежать в одній площині, то точка називається звичайною точкою поверхні (9.21), а згадана площина – дотичною площиною до поверхні в точці .

Нормальний вектор дотичної площини називається вектором нормалі до поверхні (9.21) у точці (рис. 9.12).

Р И С 9. 12 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Теорема. У кожній точці скалярного поля його градієнт (якщо він не дорівнює ) спрямований по нормалі до поверхні рівня, яка проходить через цю точку. Справді, розглянемо яку – небудь (будь – яку ) ????????? дотичну пряму до поверхні рівня (рис. 9.13), позначимо її напрямний вектор . Тоді , то вздовж поверхні рівня має стале значення. Але за формулою (9.20) , отже проекція на напрям дорівнює нулю, тобто (нагадаємо, що за умовою теореми ).

Р И С, 9.13 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Таким чином ненульовий вектор перпендикулярний до всіх дотичних прямих до поверхні рівня в точці . Значить усі дотичні прямі лежать в одній площині, яка є дотичною площиною до поверхні рівня, а вектор є нормальним вектором цієї площини, тобто вектором нормалі до поверхні рівня в точці .

Наслідок. Вектор нормалі до поверхні в точці можна знайти як

. (9.22)

Це безпосередньо випливає з щойно доведеної теореми, бо поверхня є поверхнею рівня для поля .

Отже всі точки поверхні , в яких існує , є звичайними точками поверхні. Якщо ж у даній точці усі три похідні дорівнюють нулю, або хоч одна з них не існує, то точка є особливою точкою поверхні . У такій точці не визначена нормаль до поверхні, а значить не існує і дотична площина.

Задача. Поверхню задано рівнянням і точка . Скласти рівняння дотичної площини і рівняння нормалі до поверхні у точці .

Розв’язання. З аналітичної геометрії відомо, що рівняння площини, яка проходить через точку , має вигляд

,

де нормальний вектор площини. За формулою (9.22) нормальним вектором шуканої дотичної площини є

.

Отже рівняння цієї площини записується у вигляді

. (9.23)

Рівняння нормалі одержимо як рівняння прямої, яка проходить через точку і має напрямний вектор :

. (9.24)

Приклад. Поверхня задана рівнянням

Написати рівняння дотичної площини і нормалі до поверхні в точці .

Знайти особливі точки поверхні.

В даному прикладі .

Знаходимо частинні похідні і обчислюємо їх значення в точці :

.

Тоді

.

Рівняння дотичної площини (формула (9.23)):

Після скорочення і зведення подібних отримуємо

.

Рівняння нормалі запишемо як рівняння перпендикуляра до дотичної поверхні в точці (формула (9.24)):

.

Щоб знайти координати особливих точок поверхні, прирівнюємо до нуля частинні похідні функції і розв’язуємо одержану систему рівнянь:

Система має два розв’язки, яким відповідають дві точки . Точка не лежить на заданій поверхні (її координати не задовольняють рівняння поверхні), а точка належить до поверхні. Отже задана поверхня має одну особливу точку .

9.10. Частинні похідні і повні диференціали вищих порядків.

Розглянемо для визначеності функцію двох змінних (для випадку більшого числа аргументів усі міркування будуть аналогічними). Нехай ця функція має частинні похідні у кожній точці деякої області . Тоді ці частинні похідні самі є функціями, заданими в області , і в свою чергу можуть мати частинні похідні.

Означення. Частинна похідна від частинної похідної даної функції називається частинною похідною другого порядку даної функції.

Функція двох змінних може мати чотири частинні похідні другого порядку, які позначаються так:

;

;

;

.

Аналогічно визначаються частинні похідні третього і більш високих порядків. Наприклад

.

Обчислення частинних похідних вищих порядків виконується за звичайними правилами диференціювання.

Приклад. Знайти частинні похідні другого порядку функції

.

Обчислюємо:

;

:

;

;

;

.

Зазначимо, що в даному прикладі , тобто значення мішаної похідної не залежало від порядку, в якому проводилося диференціювання. Умови, при яких має місце рівність мішаних похідних, формулює наступна теорема.

Теорема. (про незалежність від порядку диференціювання). Якщо мішані частинні похідні, що відрізняються лише порядком диференціювання, неперервні, то вони рівні між собою.

Наприклад, .

Подібно до частинних похідних визначаються і повні диференціали вищих порядків.

Означення. Повний диференціал від повного диференціала функції називається повним диференціалом другого порядку даної функції.

Аналогічно визначаються повні диференціали третього і вищих порядків. Отже, повний диференціал другого порядку (в припущенні неперервності мішаних похідних):

. (9.25)

Подібним чином одержимо

. (9.26)

Формули (9.25) і (9.26) можна символічно записати так:

,

де в правій частині слід розкрити дужки так, ніби є звичайними алгебраїчними множниками.

Цей символічний запис узагальнюється за індукцією на випадок повного диференціала будь – якого порядку :

. (9.27)

Зазначимо, що формули (9.25 – 9.27) справедливі лише для випадку, коли аргументи функції є незалежними змінними.