
- •Поняття про визначник. Властивості визначників.
- •Поняття про визначник іі порядку.
- •Визначник ііі порядку.
- •Визначник - го порядку.
- •Властивості визначників
- •Мінори та алгебраїчні доповнення елемента визначника.
- •Теорема Лапласа та її наслідки.
- •Поняття про матрицю. Види матриць.
- •Поняття про матрицю
- •Дії над матрицями
- •Властивості дій над матрицями
- •Обернена матриця.
- •Означення рангу матриці.
- •Елементарні перетворення матриць.
- •Обчислення рангу матриці.
- •Поняття лінійної залежності.
- •Теорема про ранг матриці.
- •Поняття про слар та її розв’язки.
- •Поняття про систему рівнянь та її розв’язки.
- •Сумісність слар. Теорема Кронекера-Капеллі.
- •Методи розв’язання слар
- •Правило Крамера розв’язуванння системи n рівнянь з n невідомими.
- •Матричний метод розв‘язування систем n лінійних рівнянь з n невідомими.
- •Метод Гауса.
- •Класифікація систем за кількістю розв’язків.
Методи розв’язання слар
Правило Крамера розв’язуванння системи n рівнянь з n невідомими.
Застосуємо визначники та їх властивості до розв’язування системи трьох лінійних рівнянь з трьома невідомими.
Нехай дано систему трьох лінійних рівнянь з трьома невідомими:

де
![]() -
коефіцієнти системи,
-
коефіцієнти системи,
![]() -
вільні члени. Якщо
-
вільні члени. Якщо
![]() ,
система називається однорідною,
якщо хоч один вільний член відмінний
від нуля, – неоднорідною.
Розв’язком системи називається будь-яка
трійка чисел
,
система називається однорідною,
якщо хоч один вільний член відмінний
від нуля, – неоднорідною.
Розв’язком системи називається будь-яка
трійка чисел
![]() ,
що перетворює рівняння системи в
тотожності.
,
що перетворює рівняння системи в
тотожності.
Розглянемо визначник 3-го порядку, складений з коефіцієнтів при невідомих, назвемо його основним визначником системи:

Введемо також наступні позначення:
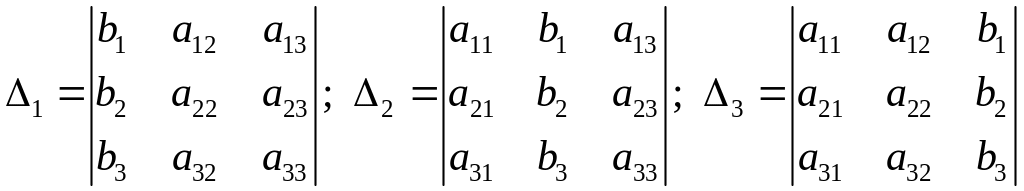 ,
,
Припустивши,
що![]() ,
одержимо єдиний розв’язок системи:
,
одержимо єдиний розв’язок системи:

Підставляючи
знайдені значення
![]() в рівняння системи, переконуємося, що
кожне з рівнянь перетворюється в
тотожність. Пропонується зробити це
самостійно.
в рівняння системи, переконуємося, що
кожне з рівнянь перетворюється в
тотожність. Пропонується зробити це
самостійно.
Теорема (правило) Крамера. Якщо визначник системи не дорівнює нулю, то система має єдиний розв’язок, який розв’язок знаходимо за формулами:
,
де
-
головний визначник системи, а
![]() – визначники, одержані з нього заміною
відповідно І, ІІ, ІІІ, стовпця вільними
членами.
– визначники, одержані з нього заміною
відповідно І, ІІ, ІІІ, стовпця вільними
членами.
Приклад.
Розв’язати систему рівнянь:

Розв’язання.

Нехай
головний визначник системи дорівнює
нулю. Якщо при цьому хоч один з визначників
![]() не дорівнює нулеві, то система несумісна.
не дорівнює нулеві, то система несумісна.
Дійсно,
якщо
![]() ,
то
,
то
![]() не виконується при кожному значенні
не виконується при кожному значенні![]() .
Якщо
.
Якщо![]() ,
то система або не має розв’язку, або
має незчислену множину розв’язків.
,
то система або не має розв’язку, або
має незчислену множину розв’язків.
Ми
записали формули Крамера для розв’язування
системи трьох рівнянь з трьома невідомими,
ці формули справедливі і для n рівнянь
з n невідомими, якщо
![]() :
:

 .
.
Матричний метод розв‘язування систем n лінійних рівнянь з n невідомими.
Розглянемо систему n лінійних рівнянь з n невідомими:
Виведемо наступні позначення
 ;
;
Отже,
– матриця коефіцієнтів при невідомих,
![]() – матриця-стовпчик із невідомих,
– матриця-стовпчик вільних членів.
– матриця-стовпчик із невідомих,
– матриця-стовпчик вільних членів.
Тоді
систему
лінійних рівнянь з
невідомими можна записати у матричній
формі
![]() або:
або:
![]()

Дійсно, виконавши множення в лівій частині, одержимо
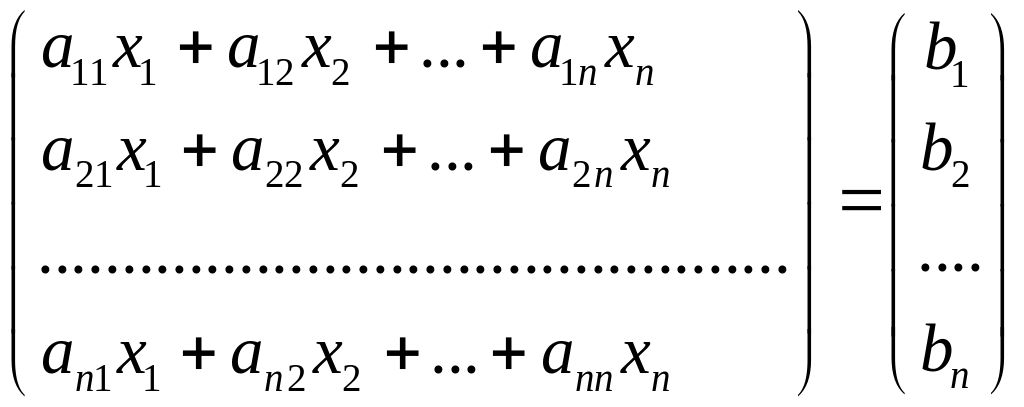
Пригадавши означення рівності двох матриць одержимо дану систему рівнянь з невідомими.
Розв’язування матричних рівнянь.
Рівність
![]() являє собою матричне рівняння, в якому
невідома матриця – стовпчик
.
Це рівняння можна розв’язати, якщо
матриця
– неособлива (тобто визначник системи
не дорівнює нулю). В цьому випадку для
матриці
існує обернена матриця
являє собою матричне рівняння, в якому
невідома матриця – стовпчик
.
Це рівняння можна розв’язати, якщо
матриця
– неособлива (тобто визначник системи
не дорівнює нулю). В цьому випадку для
матриці
існує обернена матриця
![]() .
Помноживши обидві частини матричного
рівняння на
зліва одержимо:
.
Помноживши обидві частини матричного
рівняння на
зліва одержимо:
![]()
Останнюрівність називають розв’язком системи в матричній формі. Невідома матриця виражена через відомі матриці і .
Приклад. Розв’язати систему:
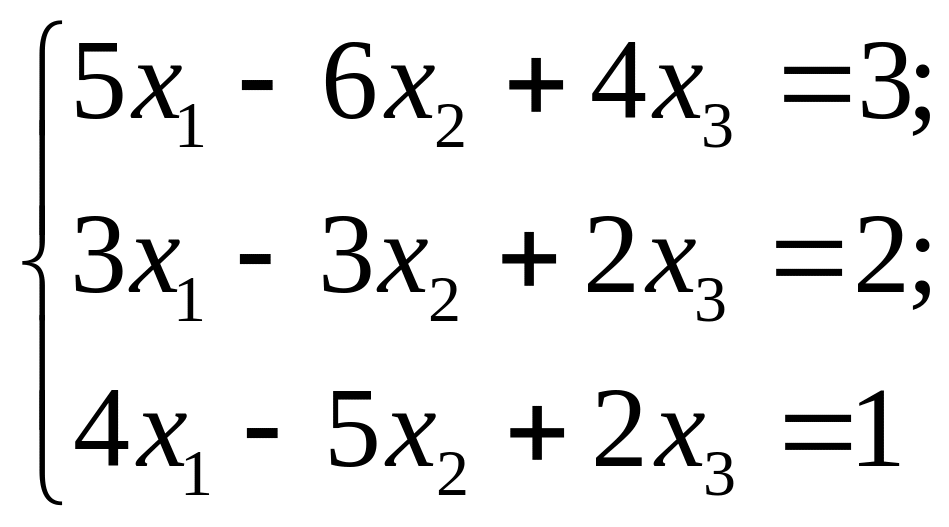
Розв’язання.
 ;
;




тоді маємо обернену матрицю та шуканий розв’язок:
 ;
;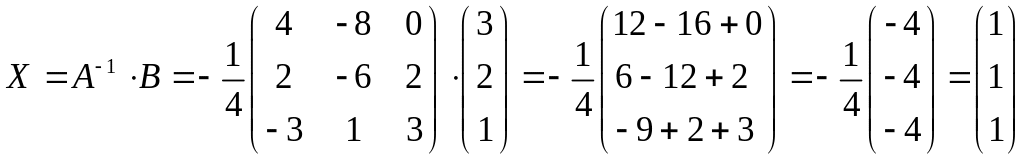
Відповідь:
![]()
Метод Гауса.
Метод Гаусса розв’язування системи т лінійних рівнянь з п невідомими являє собою метод послідовного виключення змінних з рівнянь системи. Розв’язання СЛАР методом Гаусса можна умовно розділити на 2 етапи: прямий та зворотний хід.
Прямий хід методу Гауса саме і полягає в послідовному виключенні змінних (невідомих) з рівнянь системи.
Не
порушуючи загальності, будемо вважати,
що
![]() ,
в іншому випадку можна переставити
невідомі. Отже, маємо систему:
,
в іншому випадку можна переставити
невідомі. Отже, маємо систему:

Перший
крок: за допомогою першого (робочого)
рівняння з усіх наступних рівнянь
виключимо х1,
для чого перше помножимо на
![]() і віднімемо від другого, потім – на
і віднімемо від другого, потім – на
![]() і віднімемо від третього і т.д. Одержимо
систему, еквівалентну даній:
і віднімемо від третього і т.д. Одержимо
систему, еквівалентну даній:

Припустивши,
що
![]() ,
аналогічно виключимо
,
аналогічно виключимо
![]() з
третього і наступних рівнянь (перше
рівняння на даному етапі вже виконало
свою місію і в подальших перетвореннях
участі не бере, а переписується без
змін; робочим тепер є друге рівняння).
з
третього і наступних рівнянь (перше
рівняння на даному етапі вже виконало
свою місію і в подальших перетвореннях
участі не бере, а переписується без
змін; робочим тепер є друге рівняння).
Продовжуючи процес послідовного виключення невідомих, ми побачимо, що система набуває простішого виду.
Пропускаючи деякі моменти, зауважимо, що зворотний хід методу починається з відшукання (або вираження) певної змінної із останнього рівняння системи , після чого знаходять значення інших змінних (або виразів для них), послідовно повертаючись від останнього до першого рівняння.
