
- •Свойства:
- •2 Степенным рядом называется ряд вида
- •2. Структура общего решения.
- •2.Общее решение линейного однородного дифференциального
- •2.Дифференциальные уравнения первого порядка.
- •2…. Определение. Нахождение решения уравнения , удовлетворяющего начальным условиям , называется решением задачи Коши.
- •. Тригонометрическая подстановка.
- •2…… Однородные уравнения.
- •2….. Линейные уравнения.
№1 1Понятие первообразной, неопределенного интеграла.
Функция
F(x)
называется первообразной для функции
f(x)
если F’(x)=
f(x)
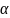 F(x)
=f(x)dx.
Отыскание первообразной функции по
заданной ее производной, обратное
дифференцирование- интегрирование.
F(x)
=f(x)dx.
Отыскание первообразной функции по
заданной ее производной, обратное
дифференцирование- интегрирование.
Совокупность первообразных для функции f(x) или от дифференциала f(x) называется неопределенным интегралом и обозначается Sf(x)dx=F(x)+c, если de F(x)+C=f(x)dx.
Свойство неопределенного интеграла: 1. Неопределенный интеграл от дифференциала функции равен этой функции f произвольная константа: SdF(x)=F(x)+C 2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции: Sf(x)dx=f(x)dx Sf(x)dx=f(x) 3. Неопределенный интеграл алгебраической сумме неопределенных интегралов этих функций: S[F(x)+φ(x)]dx=Sf(x)dx+Sφ(x)dx 4.постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:Saf(x)dx=aSf(x)dx
Табличные интегралы:
Sdx=x+c
Sxndx=
Sexdx=ex+c
Ssindx=-cosx+c
Scosxdx=sinx+c
1.2
Числовой
ряд содержащий бесконечное множество
положительных и бесконечное множество
отрицательных членов, называются
знакопеременными. Частные случаем
знакопеременного рядя является
знакочередующийся ряд, в котором
последовательные члены имеют
противоположные знаки. Признак Лейбница.
Для знакочередующихся рядом действует
достаточный признак сходимости Лейбница.
Пусть{an}
является числовой последовательностью,
такой, что 1. An+1<an
для всех n;
2. Limn→∞an=0.
Тогда знакочередующиеся ряды
 тan
и
тan
и

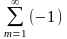 n-1an
сходятся. Абсолютная и условная
сходимость. Ряд
n-1an
сходятся. Абсолютная и условная
сходимость. Ряд
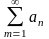 называется
абсолютно сходящимися, если ряд
называется
абсолютно сходящимися, если ряд
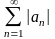 Так
же сходятся. Если ряд
Так
же сходятся. Если ряд
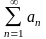 сходятся абсолютно, то он является
сходящимся. Обратное утверждение не
верно. Ряд
называется
условно сходящими, если сам он сходится,
а ряд, составленный из модулей членов,
расходится.
сходятся абсолютно, то он является
сходящимся. Обратное утверждение не
верно. Ряд
называется
условно сходящими, если сам он сходится,
а ряд, составленный из модулей членов,
расходится.
3.
№2 1 Свойство неопределенного интеграла: 1. Неопределенный интеграл от дифференциала функции равен этой функции f произвольная константа: SdF(x)=F(x)+C 2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции: Sf(x)dx=f(x)dx Sf(x)dx=f(x) 3. Неопределенный интеграл алгебраической сумме неопределенных интегралов этих функций: S[F(x)+φ(x)]dx=Sf(x)dx+Sφ(x)dx 4.постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:Saf(x)dx=aSf(x)dx
2. Абсолютная и условная сходимость. Ряд называется абсолютно сходящимися, если ряд Так же сходятся. Если ряд сходятся абсолютно, то он является сходящимся. Обратное утверждение не верно. Ряд называется условно сходящими, если сам он сходится, а ряд, составленный из модулей членов, расходится.
3.
№3
1.1.
Sdx=x+c 2. Sxndx=
3. S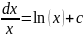 4. Sandx=
4. Sandx=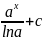 5. Sexdx=ex+c
6. Ssinxdx=-cosx+c 7. Scosxdx=sinx+c 8.
5. Sexdx=ex+c
6. Ssinxdx=-cosx+c 7. Scosxdx=sinx+c 8. 9.
9.
 10.
10.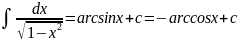 11.
11. 12.
12.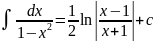 13.
13.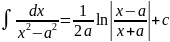 14.
14.
 15.
15.
 16.
16.
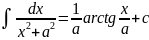 Примеры
решений с помощью табличных значений.
Примеры
решений с помощью табличных значений.
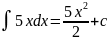 2
2
 3
3
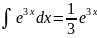
2.
Функциональный ряд
 называется
сходящимся
в точке (х=х0),
если в этой точке сходится последовательность
его частных сумм. Предел последовательности
называется
сходящимся
в точке (х=х0),
если в этой точке сходится последовательность
его частных сумм. Предел последовательности
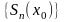 называется
суммой ряда
в точке х0.
называется
суммой ряда
в точке х0.
Если членами ряда будут не числа, а функции от х, то ряд называется функциональным.
Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится.
Совокупность таких значений называется областью сходимости.
Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:
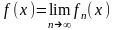
№4 Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают:
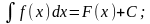
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1.
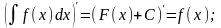
2.
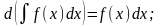
3.
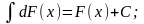
4.
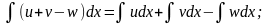 где u,
v,
w
– некоторые функции от х.
где u,
v,
w
– некоторые функции от х.
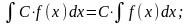
Приме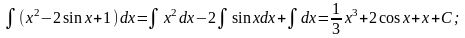 Для удобства значения неопределенных
интегралов большинства элементарных
функций собраны в специальные таблицы
интегралов, которые бывают иногда
весьма объемными. В них включены
различные наиболее часто встречающиеся
комбинации функций. Но большинство
представленных в этих таблицах формул
являются следствиями друг друга, поэтому
ниже приведем таблицу основных
интегралов, с помощью которой можно
получить значения неопределенных
интегралов различных функций.
.1.
Sdx=x+c 2. Sxndx=
3. S
4. Sandx=
5. Sexdx=ex+c
6. Ssinxdx=-cosx+c 7. Scosxdx=sinx+c 8.
9.
10.
11.
12.
13.
14.
15.
16.
Для удобства значения неопределенных
интегралов большинства элементарных
функций собраны в специальные таблицы
интегралов, которые бывают иногда
весьма объемными. В них включены
различные наиболее часто встречающиеся
комбинации функций. Но большинство
представленных в этих таблицах формул
являются следствиями друг друга, поэтому
ниже приведем таблицу основных
интегралов, с помощью которой можно
получить значения неопределенных
интегралов различных функций.
.1.
Sdx=x+c 2. Sxndx=
3. S
4. Sandx=
5. Sexdx=ex+c
6. Ssinxdx=-cosx+c 7. Scosxdx=sinx+c 8.
9.
10.
11.
12.
13.
14.
15.
16.
2 Степенным рядом называется ряд вида
 .
.
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Теорема.
Если степенной
ряд
сходится при x
= x1
, то он сходится и притом абсолютно для
всех
 .
.
Таким
образом, если степенной ряд
 сходится
в точке х1,
то он абсолютно сходится в любой точке
интервала длины 2
сходится
в точке х1,
то он абсолютно сходится в любой точке
интервала длины 2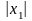 с центром в точке х
= 0.
с центром в точке х
= 0.
Следствие.
Если при х =
х1
ряд расходится, то он расходится для
всех
 .
.
Таким
образом, для каждого степенного ряда
существует такое положительное число
R,
что при всех х
таких, что
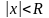 ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех
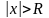 ряд
расходится. При этом число R
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
ряд
расходится. При этом число R
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.
Радиус сходимости может быть найден по формуле:
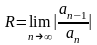
№5 1. И 2 С помощью степенных рядов возможно интегрировать дифференциальные уравнения.
Рассмотрим линейное дифференциальное уравнение вида:
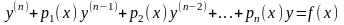 Если
все коэффициенты и правая часть этого
уравнения разлагаются в сходящиеся в
некотором интервале степенные ряды,
то существует решение этого уравнения
в некоторой малой окрестности нулевой
точки, удовлетворяющее начальным
условиям.
Если
все коэффициенты и правая часть этого
уравнения разлагаются в сходящиеся в
некотором интервале степенные ряды,
то существует решение этого уравнения
в некоторой малой окрестности нулевой
точки, удовлетворяющее начальным
условиям.
Это решение можно представить степенным рядом:
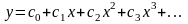
Для нахождения решения остается определить неизвестные постоянные ci.
Эта задача решается методом сравнения неопределенных коэффициентов. Записанное выражение для искомой функции подставляем в исходное дифференциальное уравнение, выполняя при этом все необходимые действия со степенными рядами (дифференцирование, сложение, вычитание, умножение и пр.)
Затем приравниваем коэффициенты при одинаковых степенях х в левой и правой частях уравнения. В результате с учетом начальных условий получим систему уравнений, из которой последовательно определяем коэффициенты ci.
Отметим, что этот метод применим и к нелинейным дифференциальным уравнениям. Существует и другой метод решения дифференциальных уравнений с помощью рядов. Он носит название метод последовательного дифференцирования.
Рассмотрим тот же пример. Решение дифференциального уравнения будем искать в виде разложения неизвестной функции в ряд Маклорена.

Если
заданные начальные условия y(0)=1,
y’(0)=0
подставить
в исходное дифференциальное уравнение,
получим, что
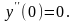
Далее
запишем дифференциальное уравнение в
виде
 и будем последовательно дифференцировать
его по х.
и будем последовательно дифференцировать
его по х.
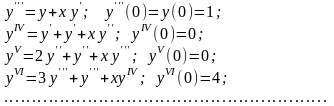
После подстановки полученных значений получаем:
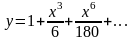
№6. 1. Рассмотрим три основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Способ подстановки (замены переменных).
Теорема:
Если требуется найти интеграл
 ,
но сложно отыскать первообразную, то
с помощью замены x
= (t)
и dx
= (t)dt
получается:
,
но сложно отыскать первообразную, то
с помощью замены x
= (t)
и dx
= (t)dt
получается:

Доказательство: Продифференцируем предлагаемое равенство:
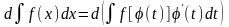
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[(t)](t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv) = uv + vu
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав,
получаем:
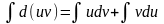 ,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
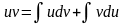 или
или
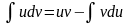 ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример.
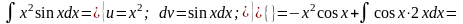

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
