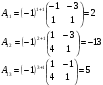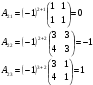контрольная работа №1 - вариант 2 - 1й семестр
.docxКонтрольная работа № 1
Вариант 2
Задание 1-10.
Даны три комплексных числа

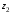 и
и
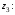
1) выполните действия над ними в алгебраической, тригонометрической и показательной формах;
2) найдите
расстояние между точками
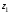 и
и
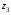 на комплексной плоскости.
на комплексной плоскости.
2.
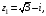
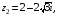
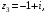

Решение:
-
Найдем значение
 в алгебраической форме
в алгебраической форме
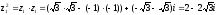
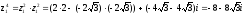
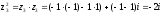

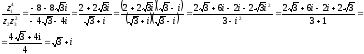
Найдем
значение
 в
тригонометрической форме
в
тригонометрической форме
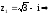

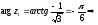

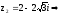
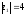

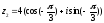

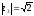
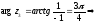
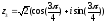
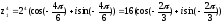
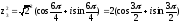
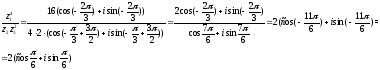
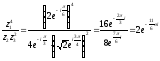
Вычислим
значение
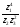 в
показательной форме
в
показательной форме



2) Найдем расстояние
между точками
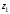 и
и
 на комплексной плоскости:
на комплексной плоскости:
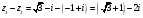
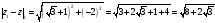
Задания 11 – 20. Решите уравнение на множестве комплексных чисел.
12.
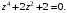
Решение.
Сделаем замену z2=t, получим уравнение:
t2+2t+2=0
t1=-1-i
t2=-1+i
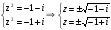
Приведем числа к тригонометрической форме


Задания 21 – 30. Решите систему уравнений тремя способами:
1) методом Крамера;
2) методом обратной матрицы;
3) методом Гаусса.
22.
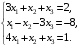
Решение.
1)Для решения системы по правилу Крамера найдем следующие определители:
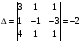
Так как данный определитель не равен нулю, то данная система имеет единственное решение, а значит система совместна.
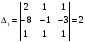


Тогда решение системы находим по формулам:
х1
=
 = -1; х2
=
= -1; х2
=
 = 4; х3
=
= 4; х3
=
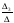 =1
=1
-
Решим систему линейных уравнений матричным методом.
Обозначим A
=
 ,
X
=
,
X
=
 ,
B
=
,
B
=
 .
Тогда данную систему можно записать в
виде: АХ=В. Т.к. матрица невырожденная
(Δ=-2), то X
= A-1B.
.
Тогда данную систему можно записать в
виде: АХ=В. Т.к. матрица невырожденная
(Δ=-2), то X
= A-1B.
Вычислим обратную
матрицу
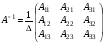 .
.
Определитель
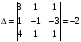
|
|
|
|
Тогда A-1
=

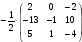
Получим X
= A-1B
=
 =
=
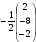 =
=
3)Для решения системы методом Гаусса приведем матрицу к треугольному виду
Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:
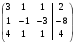 =
[поменяем местами первую и вторую
строчки] =
=
[поменяем местами первую и вторую
строчки] =
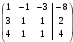 = [умножаем первую строчку на -3 и складываем
со второй, умножаем первую на -4 и
складываем с третьей] =
= [умножаем первую строчку на -3 и складываем
со второй, умножаем первую на -4 и
складываем с третьей] =
 = умножаем вторую строку на -
= умножаем вторую строку на - и складываем с третьей] =
и складываем с третьей] =
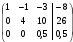
Получаем систему:
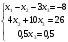
Получаем х1=-1, х2=4, х3=1.
Ответ: х1=-1, х2=4, х3=1
Задания 31 – 40.
Даны три вектора
 и
и
 Докажите, что векторы
Докажите, что векторы
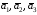 образуют базис, и определите, какая это
тройка векторов: правая или левая.
образуют базис, и определите, какая это
тройка векторов: правая или левая.
32.
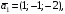
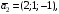
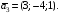
Решение.
Векторы a, b, c образуют базис в пространстве R3 в том случае, если равенство a + b + c = 0 выполняется лишь тогда, когда = = = 0.
Рассмотрим это условие:
(1;-1;-2) + (2;1;-1) + (3;-4;1) = (0;0;0) или
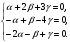
Рассмотрим матрицу данной системы и приведем ее к треугольному виду:

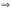 Умножим
первую строку на 2 и сложим с третьей,
сложим первую строку со второй ;
Умножим
первую строку на 2 и сложим с третьей,
сложим первую строку со второй ;
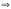

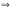 Умножим вторую строку на –1 и сложим
с третьей
Умножим вторую строку на –1 и сложим
с третьей
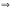

Так как число ненулевых строк в треугольной матрице равно числу переменных, то система имеет единственное решение, а именно = = = 0. Значит, векторы a, b, c образуют базис.
Найдем смешанное произведение векторов

Cмешанное
произведение векторов не равно 0, то
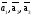 образуют базис, и так как
образуют базис, и так как
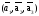 >0,
то тройка векторов является правой.
>0,
то тройка векторов является правой.
Задания 41 – 50.
Даны координаты вершин треугольной
пирамиды
 Найдите:
Найдите:
1) угол между
ребрами
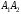 и
и
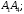
2) площадь
грани

3) длину высоты,
опущенной из вершины
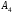 на грань
на грань

4) уравнение
прямой, проходящей через ребро

5) уравнение
плоскости, которой принадлежит грань

6) массу
материальной треугольной пирамиды
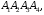 изготовленной из меди плотностью
изготовленной из меди плотностью
 (считая, что 1 масштабная единица в
системе координат равна 1 см).
(считая, что 1 масштабная единица в
системе координат равна 1 см).
42.



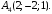
-
Известно, что косинус угла меду двумя векторами
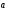 и
и
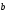 определяется
по формуле
определяется
по формуле
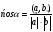
Координаты вектора
 (-1;
2;4) ,
(-1;
2;4) ,
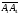 (-1; -3; 4)
(-1; -3; 4)

-
площадь треугольника, построенного на векторах
 и
и
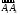 вычисляется по формуле
вычисляется по формуле
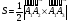 .
.
А1А2 (–1; 2; 4),
А1А3 (1–3; 2–1; 3–(–3))
А1А3 (–2; 1; 6)
Векторное произведение векторов
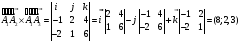

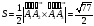 (ед.
кв.)
(ед.
кв.)
3)Найдем уравнение плоскости А1А2А3
 или
или

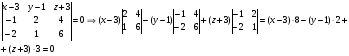
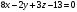 -уравнение
плоскости основания А1А2А3
-уравнение
плоскости основания А1А2А3
4)Расстояние от т.А4(2;-2;1) до плоскости А1А2А3 находится по формуле

5) Уравнение прямой А1А2
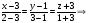
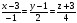 искомое уравнение
искомое уравнение
6) Вычислим объем пирамиды А1А2А3А4
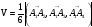
 (ед3)
(ед3)
Масса материальной
треугольной пирамиды
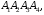 изготовленной из меди плотностью
изготовленной из меди плотностью
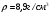
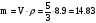 г.
г.
Задания 51 – 60. Изобразите геометрическое место точек, заданных уравнением:
1) на плоскости;
2) в пространстве.
52.

1) Преобразуем
выражение
 к виду
к виду
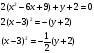
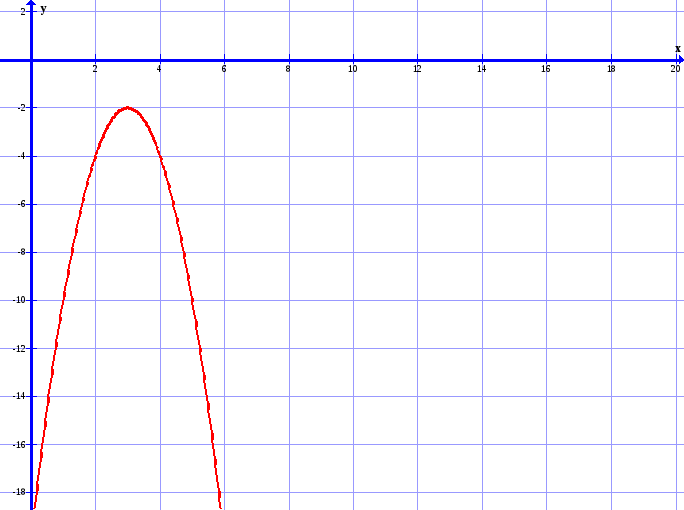
Это уравнение задает параболу с осью симметрии параллельную Оу и вершиной в точке (3;-2).
2) В пространстве 3то уравнение параболического цилиндра