
К.р. № 7 в. 6 Ряды
.docВысшая математика. Контрольная работа №7.
Тема: Ряды.
316. Исследовать сходимость числового ряда:

Решение.
Каждый член данного положительного ряда меньше предыдущего, поэтому для исследования сходимости используем интегральный признак:
![]() .
.
Решим сначала соответствующий неопределённый интеграл:
 .
.
Тогда, получим:
 ,
поэтому данный ряд сходится.
,
поэтому данный ряд сходится.
Ответ: сходится.
326. Найти интервал сходимости степенного ряда:

Решение.
Находим интервал сходимости ряда:
![]() .
.
Следовательно,
![]() – искомый интервал сходимости.
– искомый интервал сходимости.
Проверяем сходимость ряда на концах интервала.
При
![]() имеем знакопеременный числовой ряд с
общим членом:
имеем знакопеременный числовой ряд с
общим членом:
![]() .
.
Поскольку с увеличением порядкового номера члены ряда убывают по абсолютной величине, а также
![]() ,
то за теоремой Лейбница ряд сходится.
,
то за теоремой Лейбница ряд сходится.
При
![]() имеем числовой ряд с общим членом:
имеем числовой ряд с общим членом:
![]() .
.
Составляем частичные суммы ряда:
![]()
![]()
![]()
Используя определение сходящегося ряда, получим:
![]() ,
поэтому ряд сходится.
,
поэтому ряд сходится.
Ответ:
![]() .
.
336. Вычислить определенный интеграл с точностью до 0,001. Для этого подынтегральную функцию следует разложить в ряд, который затем почленно проинтегрировать:
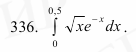
Решение.
Используя
известное разложение функции
![]() в ряд:
в ряд:
![]() разложим
подынтегральную функцию в соответствующий
ряд (для этого умножим известное
разложение в ряд почленно на
разложим
подынтегральную функцию в соответствующий
ряд (для этого умножим известное
разложение в ряд почленно на![]() ):
):
![]()
Тогда, получим:
![]()


Проводим соответствующие вычисления с заданной точностью:
 ,
,
![]() ,
,
 ,
,
![]() ,
,
 ,
,
![]() ,
,
 ,
,
![]() ,
,
 .
.
Поскольку
![]() ,
то
,
то
![]()
Ответ:
![]() .
.
346. Найти три первых отличных от нуля члена разложения в степенной ряд решения y=y(x) дифференциального уравнения, удовлетворяющего начальному условию y(0)=y0:
![]()
Решение.
Пусть
решение данного дифференциального
уравнения
![]() можно представить в виде степенного
ряда по степеням
можно представить в виде степенного
ряда по степеням
![]() :
:
![]()
По
условию
![]() ,
тогда:
,
тогда:
![]() (*).
(*).
Найдем коэффициенты ряда.
Из
условия
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Дифференцируем обе части дифференциального уравнения:
![]() ;
;
![]() ;
;
![]() ;
;
Подставим найденные коэффициенты в (*):
![]()
![]()
Ответ:
![]() .
.
356. На интервале (-π, π) задана периодическая с периодом 2π функция f(x). Требуется:
1). Разложить функцию f(x) в ряд Фурье;
2). Построить график суммы ряда Фурье.
![]()
Решение.
1).
Рядом Фурье для функции
![]() в интервале
в интервале
![]() называется тригонометрический ряд
называется тригонометрический ряд
![]() ,
,
где
коэффициенты ряда
![]() ,
,
![]() ,
,
![]() (n=1,
2, 3,…) вычисляются по формулам Фурье:
(n=1,
2, 3,…) вычисляются по формулам Фурье:
![]() ;
;
![]() ,
(n=1,
2, 3,…);
,
(n=1,
2, 3,…);
![]() ,
(n=1,
2, 3,…).
,
(n=1,
2, 3,…).
В
нашем случае:
![]() ,
,
![]() .
Находим по формулам соответствующие
коэффициенты.
.
Находим по формулам соответствующие
коэффициенты.
 .
.


![]() .
.


![]()
![]() .
.
Тогда, получим следующее разложение функции в ряд Фурье:
![]() ,
(n=1,
2, 3,…).
,
(n=1,
2, 3,…).
2). Построим график суммы ряда Фурье для третьей частичной суммы:
![]() .
.
О

![]() ,
(n=1,
2, 3,…).
,
(n=1,
2, 3,…).
