Методи та алгоритми аналізу на макрорівні;
Вибір методів аналізу в часовій області. Аналіз процесів у проектованих об'єктах можна робити в часовій і частотній областях. Аналіз у часовій області (динамічний аналіз) дозволяє одержати картину перехідних процесів, оцінити динамічні властивості об'єкта, вона є важливою процедурою при дослідженні як лінійних, так і нелінійних систем. Аналіз у частотній області більш специфічний, його застосовують, як правило, до об'єктів з лінеаризованими ММ при дослідженні коливальних стаціонарних процесів, аналізі стійкості, і т.п.
Методи аналізу в часовій області, які використовуються в універсальних програмах аналізу в САПР, — це чисельні методи інтегрування систем звичайних диференціальних рівнянь (СОДУ):
F(d/dt, V, t) = 0.
Інакше кажучи, це методи алгебрування диференціальних рівнянь. Формули інтегрування СОДУ можуть входити в ММ незалежно від компонентних рівнянь, або бути інтегрованими в ММ компонентів, як це виконано у вузловому методі.
Від вибору методу рішення СОДУ істотно залежать такі характеристики аналізу, як точність й обчислювальна ефективність. Ці характеристики визначаються насамперед типом і порядком обраного методу інтегрування СОДУ.
Застосовують два типи методів інтегрування - явні (методи, засновані на формулах інтегрування вперед), і неявні (інтерполяційні, засновані на формулах інтегрування назад). Розходження між ними зручно показати на прикладі найпростіших методів першого порядку - методів Ейлера.
Формула явного методу Ейлера являє собою наступну формулу заміни похідних у точці tn:
d/dt | n = (Vn+1 — Vn ) / hn,
де індекс дорівнює номеру кроку інтегрування; hn = tn+1 - tn — розмір кроку інтегрування (звичайно hn називають просто кроком інтегрування). У формулі неявного методу Ейлера використане диферинціювання назад: d/dt | n = (Vn — Vn-1 ) / hn, де hn = tn - tn-1.
Виконаємо порівняльний аналіз явних і неявних методів на прикладі модельного завдання:
d/dt = AV (3.23)
при ненульових початкових умовах V0 ≠0 і при використанні методів Ейлера з постійним кроком h.
Тут C — постійна матриця; V — вектор фазових змінних.
При алгебруванні явним методом маємо
(Vn+1 - Vn ) / h = A Vn
або
Vn+1 = (E + h) Vn,
де & — одинична матриця. Вектор Vn+1 можна виразити через вектор початкових умов V0: Vn+1 = (E + h)n V0. (3.24) Позначимо
B = E + h (3.25)
і застосуємо
перетворення подоби для матриці (
![]() де M —
перетворююча матриця,
diag{Bj}
-діагональна матриця із власними
значеннями Bj
матриці (
на діагоналі. Неважко
бачити, що
З лінійної алгебри
відомо, що власні значення матриць,
зв'язаних
арифметичними операціями, виявляються
зв'язаними
такими ж перетвореннями. Тому з (3.25)
треба
де M —
перетворююча матриця,
diag{Bj}
-діагональна матриця із власними
значеннями Bj
матриці (
на діагоналі. Неважко
бачити, що
З лінійної алгебри
відомо, що власні значення матриць,
зв'язаних
арифметичними операціями, виявляються
зв'язаними
такими ж перетвореннями. Тому з (3.25)
треба
![]() Точне рішення
модельного завдання
(3.23) V(t)
→0 при t→∞,
отже, умовою стійкості
процесу чисельного рішення
можна вважати
Точне рішення
модельного завдання
(3.23) V(t)
→0 при t→∞,
отже, умовою стійкості
процесу чисельного рішення
можна вважати
![]() звідки послідовно
одержуємо
звідки послідовно
одержуємо
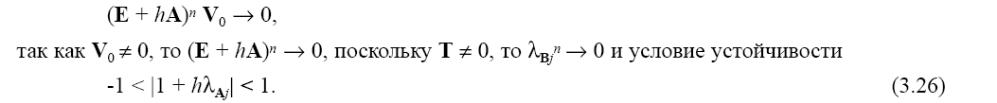
Відомо, що для фізично стійких систем власні значення матриці коефіцієнтів у ММС виявляються негативними. Якщо до того ж всі Cj речовинні величини (характер процесів у ММС із моделлю (3.23) аперіодичний), те природно визначити постійні часу фізичної системи як
![]()
і умова (3.26) конкретизується в такий спосіб
![]()
Або
![]()
де
![]() — мінімальна постійна часу.
Якщо використати
явні методи більше
високого порядку, то може збільшитися
коефіцієнт перед
(3.27), але це принципово не міняє
оцінки явних методів.
— мінімальна постійна часу.
Якщо використати
явні методи більше
високого порядку, то може збільшитися
коефіцієнт перед
(3.27), але це принципово не міняє
оцінки явних методів.
Якщо порушено умову (3.27), то відбувається втрата стійкості обчислень, а це означає, що в рішенні завдання виникають помилкові коливання з амплітудою, що збільшується від кроку до кроку, і швидким переповненням розрядної сітки. Звичайно, ні про яку адекватність рішення говорити не доводиться.
Для дотримання (3.27) застосовують ті або інші алгоритми автоматичного вибору кроку. Відзначимо, що в складній моделі розрахунок ?min для безпосереднього вибору кроку по (3.27) занадто трудомісткий, крім того, однократний розрахунок ?min мало чим допомагає, тому що в нелінійних моделях ?min може змінюватися від кроку до кроку.
Умова
(3.27) накладає тверді
обмеження на крок інтегрування. В
результаті обчислювальна ефективність
явних методів різко падає з
погіршенням обусловлености
ММС.
Справді, тривалість
![]() моделируемого
процесу повинна бути порівнянної
із часом заспокоєння системи після
збудливого впливу, тобто порівнянна з
максимальної
постійної
часу τmax. Необхідне число кроків
інтегрування дорівнює
моделируемого
процесу повинна бути порівнянної
із часом заспокоєння системи після
збудливого впливу, тобто порівнянна з
максимальної
постійної
часу τmax. Необхідне число кроків
інтегрування дорівнює
![]() Відношення
Відношення
![]() називають розкидом постійних або числом
обумовленості.
називають розкидом постійних або числом
обумовленості.
Чим
більше це число, тим гірше обумовленість.
Спроби застосування явних методів до
любым
ММС
найчастіше приводять до неприпустимо
низької обчислювальної ефективності,
оскільки в реальних моделях
![]() — звичайна ситуація. Тому в цей час в
універсальних програмах аналізу явні
методи рішення
СОДУ не застосовують.
— звичайна ситуація. Тому в цей час в
універсальних програмах аналізу явні
методи рішення
СОДУ не застосовують.
Аналогічний аналіз числової стійкості неявних методів дає наступні результати.
Замість
(3.24) маємо
![]() й умова
числової стійкості
приймає вид
й умова
числової стійкості
приймає вид
![]() яке виконується при будь-яких
h
>
0. Отже, неявний метод Ейлера
має так називану А-стійкість. Метод
інтегрування СОДУ називають K-стійким,
якщо погрішність інтегрування залишається
обмеженої
при будь-якому кроці h
>
0.
яке виконується при будь-яких
h
>
0. Отже, неявний метод Ейлера
має так називану А-стійкість. Метод
інтегрування СОДУ називають K-стійким,
якщо погрішність інтегрування залишається
обмеженої
при будь-якому кроці h
>
0.
Застосування А-стійких методів дозволяє істотно зменшити необхідні числа кроків Ш. У цих методах крок вибирається автоматично не з умов стійкості, а тільки з міркувань точності рішення.
Вибір порядку методу рішення СОДУ досить простий: по-перше, більше високий порядок забезпечує більше високу точність, по-друге, серед неявних різницевих методів, крім методу Ейлера, А-стійкі також методи другого порядку й серед них - метод трапецій. Тому переважне поширення в програмах аналізу одержали методи другого порядку - модифікації методу трапецій.
Алгоритм чисельного моделювання СОДУ. Одна із удалих реалізацій неявного методу другого порядку, яку можна вважати модифікацією методу трапецій заснована на комбінованому використанні явної й неявної формул Эйлера. Розглянемо питання, чому таке комбінування знижує погрішність і приводить до підвищення порядку методу.
Попередньо
відзначимо, що в методах "-го
порядку локальна погрішність, тобто
погрішність, допущена на одному n-м
кроці інтегрування, оцінюється старшим
зі членів, що
![]() відкидають, у розкладанні рішення
V(t)
у ряд Тейлора,
де з
- постійний коефіцієнт, що залежить від
методу
відкидають, у розкладанні рішення
V(t)
у ряд Тейлора,
де з
- постійний коефіцієнт, що залежить від
методу![]() ,
- норма
,
- норма
![]() вектора -х
похідних
V(t)
,
що оцінюється за допомогою кінцево-різницевої
апроксимації, ? — значення часу t
усередині
кроку.
вектора -х
похідних
V(t)
,
що оцінюється за допомогою кінцево-різницевої
апроксимації, ? — значення часу t
усередині
кроку.
Якщо n-й крок інтегрування в комбінованому методі був неявним, тобто виконаним по неявній формулі, то наступний крок з тим же значенням h повинен бути явним. Використовуючи розкладання рішення V(t) у ряд Тейлора на околицях крапки tn+1, одержуємо для (n+1)-го неявного кроку
![]()
і для (n+2)-го явні кроки
![]()
де
![]() —
величини
неявного і явного кроків, а значення
похідних ставляться
до моменту tn+1.
—
величини
неявного і явного кроків, а значення
похідних ставляться
до моменту tn+1.
Підставляючи (3.28) в (3.29), при h = hя = hн одержуємо:
![]()
т. е. погрішності, що обумовлюють квадратичними членами в (3.28) і (3.29) взаємно компенсуються, і старшим зі членів, що відкидають, стає член з h3. Отже, викладене комбінування неявної і явної формул Эйлера дає метод інтегрування другого порядку.
Неявні методи й, зокрема, розглянутий комбінований метод доцільно використати тільки при змінній величині кроку. Дійсно, при помітних швидкостях зміни фазових змінних погрішність залишається в припустимих межах тільки при малих кроках, у квазистатических режимах крок може бути в багато разів більше.
Алгоритми автоматичного вибору кроку засновані на порівнянні допущених і припустимої локальних погрішностей. Наприклад, уводиться деякий діапазон (коридор) погрішностей ?, у межах якого крок зберігається незмінним. Якщо ж допущена погрішність перевищує верхню границю діапазону, то крок зменшується, якщо ж виходить за нижню границю, то крок збільшується.
Методи рішення систем нелінійних алгебраїчних рівнянь. Обчислення при рішенні СОДУ складаються з декількох вкладених один в іншій циклічних процесів. Зовнішній цикл - цикл покрокового чисельного інтегрування, параметром циклу є номер кроку. Якщо модель аналізованого об'єкта нелинейна, то на кожному кроці виконується проміжний цикл - ітераційний цикл рішення системи нелінійних алгебраїчних рівнянь (СНАУ). Параметр циклу - номер ітерації. У внутрішньому циклі вирішується система лінійних алгебраїчних рівнянь (СЛАУ), наприклад, при застосуванні вузлового методу формування ММС такою системою є (3.19). Тому в математичне забезпечення аналізу на макрорівні входять методи рішення СНАУ й СЛАУ.
Для рішення СНАУ можна застосовувати прямі ітераційні методи такі, як метод простої ітерації або метод Зейделя, але в сучасних програмах аналізу найбільше поширення одержав метод Ньютона, заснований на лінеаризації СНАУ. Властиво модель (3.19) отримана саме відповідно до методу Ньютона. Основна перевага методу Ньютона - висока швидкість збіжності.
Представимо СНАУ у вигляді
![]()
Розкладаючи F(X) у ряд Тейлора на околицях деякої крапки Nk, одержуємо
![]()
Зберігаючи тільки лінійні члени, одержуємо СЛАУ з невідомим вектором N :
![]()
де
![]() Рішення
системи (3.31) дає чергове наближення до
кореня системи (3.30), що зручно позначити
Xk+1.
Рішення
системи (3.31) дає чергове наближення до
кореня системи (3.30), що зручно позначити
Xk+1.
Обчислювальний
процес стартує з
початкового наближення X0
й у випадку збіжності ітерацій
закінчується, коли погрішність, оцінювана
як
![]() стане
менше допуcтимой
погрішності ε.
стане
менше допуcтимой
погрішності ε.
Однак метод Ньютона не завжди приводить до збіжних ітерацій. Умови збіжності методу Ньютона виражаються досить складно, але існує легко використовуваний підхід до поліпшення збіжності. Це близькість початкового наближення до шуканого кореня СНАУ. Використання цього фактора привело до появи методу рішення СНАУ, називаного продовженням рішення по параметрі.
У методі продовження рішення по параметрі в ММС виділяється деякий параметр α, такий, що при α = 0 корінь Nα=0 системи (3.30) відомий, а при збільшенні α від 0 до його щирого значення складові вектора N плавно змінюються від Nα=0 до щирого значення кореня. Тоді завдання розбивається на ряд подзадач, послідовно розв'язуваних при мінливих значеннях ?, і при досить малому кроці ?? зміни ? умови збіжності виконуються.
Як параметр α можна вибрати деякий зовнішній параметр, наприклад, при аналізі електронних схем їм може бути напруга джерела живлення. Але на практиці при інтегруванні СОДУ в якості α вибирають крок інтегрування h. Очевидно, що при h = 0 корінь СНАУ дорівнює значенню вектора невідомих на попередньому кроці. Регулювання значень h покладає на алгоритм автоматичного вибору кроку.
В цих умовах очевидна доцільність подання математичних моделей для аналізу статичних станів у вигляді СОДУ, як і для аналізу динамічних режимів.
Методи
рішення
систем лінійних алгебраїчних рівнянь.
У
програмах аналізу в САПР
для рішення
СЛАУ
найчастіше застосовують метод Гаусса
або його різновиду.
Метод Гаусса
— метод послідовного виключення
невідомих
із системи рівнянь. При виключенні
k-й
невідомої
xk
із
системи рівнянь
![]() всі коефіцієнти
всі коефіцієнти
![]() при
i>k
й
j>k
перераховують
по формулі
при
i>k
й
j>k
перераховують
по формулі
![]()
Виключення n-1 невідомих, де n — порядок системи (3.32), називають прямим ходом, у процесі якого матриця коефіцієнтів здобуває трикутний вид. При зворотному ході послідовно обчислюють невідомі, починаючи з xn.
У загальному випадку число арифметичних операцій для рішення (3.32) по Гауссу пропорційно n3. Це приводить до значних витрат машинного часу, оскільки СЛАУ вирішується багаторазово в процесі одноваріантного аналізу, і істотно обмежує складність аналізованих об'єктів.
Помітно підвищити обчислювальну ефективність аналізу можна, якщо використати характерне практично для всіх додатків властивість високої розрідженості матриці C у моделі (3.32).
Матрицю називають розрідженою, якщо більшість її елементів дорівнює нулю. Ефективність обробки розріджених матриць велика тому, що, по-перше, перерахування по формулі (3.33) не потрібно, якщо хоча б один з елементів aik або akj виявляються нульовим, по-друге, не потрібні витрати пам'яті для зберігання нульових елементів. Хоча алгоритми обробки розріджених матриць більше складні, але в результаті вдається одержати витрати машинного часу, близькі до лінійних, наприклад, витрати виявляються пропорційними n1,2.
При використанні методів розріджених матриць потрібно враховувати залежність обчислювальної ефективності від того, як представлена матриця коефіцієнтів C, точніше від того, у якому порядку записані її рядки й стовпці.
Для пояснення цієї залежності розглянемо два варіанти подання однієї й тієї ж СЛАУ.
У першому випадку система рівнянь має вигляд

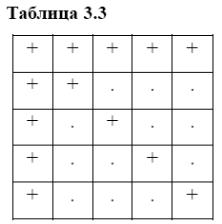
При прямому ході відповідно до формули (3.33) всі елементи матриці, які спочатку були нульовими, стають ненульовими, а матриця виявляється повністю насиченою. Елементи, що стають ненульовими в процесі гауссових виключень, називають вторинними нулями. Вторинні ненулі в таблиці 3.3 відзначені крапкою.
У другому випадку міняються місцями перше й п'яте рівняння. Матриці коефіцієнтів мають вигляд таблиць 3.3 й 3.4, де ненульові елементи представлені знайомий +. Тепер вторинні ненулі не з'являються, матриця залишається розрідженої, висока обчислювальна ефективність зберігається.
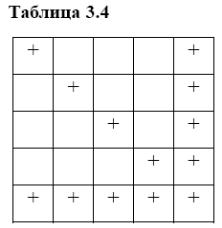
Таким чином, методи розріджених матриць повинні містити в собі способи оптимального впорядкування рядків і стовпців матриць. Використають кілька критеріїв оптимальності впорядкування. Найпростішим з них є критерій розташування рядків у порядку збільшення числа первинних ненулів, більше складні критерії враховують не тільки первинні ненулі, але й вторинні ненулі, що з'являються.
Методом розріджених матриць називають метод рішення СЛАУ на основі методу Гаусса з урахуванням розрідженості (первинної й вторинної) матриці коефіцієнтів.
Метод розріджених матриць можна реалізувати шляхом інтерпретації й компіляції. В обох випадках створюються масиви ненульових коефіцієнтів матриці (з урахуванням вторинних ненулів) і масиви координат цих ненульових елементів.
При цьому виграш у витратах пам'яті досить значний. Так, при матриці помірного розміру 200?200 без обліку розрідженості буде потрібно 320 кбайт. Якщо ж взяти характерне значення 9 для середнього числа ненулів в одному рядку, то для коефіцієнтів і покажчиків координат буде потрібно не більше 28 кбайт.
У випадку інтерпретації моделююча програма для кожної операції по (3.33) при aik ≠ 0 й akj ≠ 0 знаходить, використовуючи покажчики, потрібні коефіцієнти й виконує арифметичні операції по (3.33). Оскільки СЛАУ в процесі аналізу вирішується багаторазово, те й операції пошуку потрібних коефіцієнтів також повторюються багаторазово, на що природно витрачається машинний час.
Спосіб компіляції більше економічний по витратах часу, але уступає способу інтерпретації по витратах пам'яті. При компіляції пошук потрібних для (3.33) коефіцієнтів виконується однократно перед чисельним рішенням завдання. Замість безпосереднього виконання арифметичних операцій для кожної з них компілюється команда зі знайденими адресами ненульових коефіцієнтів.
Такі команди утворять робочу програму рішення СЛАУ, що і буде вирішуватися багаторазово.
Очевидно, що тепер у робочій програмі буде виконуватися мінімально необхідне число арифметичних операцій.
Аналіз у частотній області. Аналіз у частотній області виконується відносно лінеаризованих моделей об'єктів. Для лінійних СОДУ справедливе застосування для алгебрування диференціальних рівнянь перетворення Фур'є, у якому оператор d/dt заміняється на оператор jω.
Характерною особливістю що виходить СЛАУ є комплексний характер матриці коефіцієнтів, що до деякої міри ускладнює процедуру рішення, але не створює принципових труднощів. При рішенні задають ряд частот ωk. Для кожної частоти вирішують СЛАУ й визначають дійсні й мнимі частини шуканих фазових змінних. По них визначають амплітуду й фазовий кут кожної спектральної складової, що й дозволяє побудувати амплітудно-частотні, фазочастотні характеристики, знайти власні частоти коливальної системи й т.п.
Різноманітний аналіз. Одноваріантний аналіз дозволяє одержати інформацію про стан і поводження проектованого об'єкта в одній крапці простору внутрішніх N і зовнішніх Q параметрів. Очевидно, що для оцінки властивостей проектованого об'єкта цього недостатньо. Потрібно виконувати різноманітний аналіз, тобто досліджувати поводження об'єкта, у ряді крапок згаданого простору, що для стислості будемо далі називати простором аргументів.
Найчастіше різноманітний аналіз у САПР виконується в інтерактивному режимі, коли розроблювач неодноразово міняє в математичній моделі ті або інші параметри з безлічей N й Q, виконує одноваріантний аналіз і фіксує отримані значення вихідних параметрів. Подібний різноманітний аналіз дозволяє оцінити області працездатності, ступінь виконання умов працездатності, а отже, ступінь виконання технічного завдання (ТЗ) на проектування, розумність прийнятих проміжних рішень по зміні проекту й т.п.
Среди процедур різноманітного аналізу можна виділити типові, виконувані по заздалегідь складених програмах. До таких процедур ставляться аналіз чутливості й статистичний аналіз.
Найбільше просто аналіз чутливості реалізується шляхом чисельного диференціювання.
Нехай аналіз проводиться в деякій крапці Nном простору аргументів, у якій попередньо проведений одноваріантний аналіз і знайдені значення вихідних параметрів yjном. Виділяється N параметрів-аргументів ,i (із числа елементів векторів X й Q), вплив яких на вихідні параметри підлягає оцінити, по черзі кожний з них одержує збільшення Δxi, виконується одноваріантний аналіз, фіксуються значення вихідних параметрів yj і підраховуються значення абсолютних
![]()
і
відносних коефіцієнтів чутливості
![]() Такий
метод чисельного диференціювання
називають методом збільшень.
Для аналізу чутливості, відповідно до
методу збільшень,
потрібно виконати N+1
раз одноваріантний аналіз.
Такий
метод чисельного диференціювання
називають методом збільшень.
Для аналізу чутливості, відповідно до
методу збільшень,
потрібно виконати N+1
раз одноваріантний аналіз.
Результат його застосування — матриці абсолютної й відносної чутливості, елементами яких є коефіцієнти Aji й Bji.
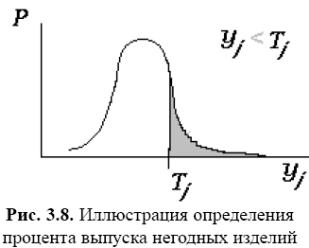
Ціль статистичного аналізу — оцінка законів розподілу вихідних параметрів й (або) числових характеристик цих розподілів. Випадковий характер величин yj обумовлений випадковим характером параметрів елементів xi, тому вихідними даними для статистичного аналізу є відомості про закони розподілу xi. Відповідно до результатів статистичного аналізу прогнозують такий важливий виробничий показник, як відсоток бракованих виробів у готовій продукції (мал. 3.8). На малюнку представлена розрахована щільність S розподілу вихідного параметра yj, що має умову працездатності yj<Tj, затемнений ділянка характеризує частку виробів, що не задовольняють умові працездатності параметра yj.
В САПР статистичний аналіз здійснюється чисельним методом Монте-Карло (статистичних випробувань). Відповідно до цього методу виконуються N статистичних випробувань, кожне статистичне випробування являє собою одноваріантний аналіз, виконуваний при випадкових значеннях параметрів-аргументів. Ці випадкові значення вибирають відповідно до заданих законів розподілу аргументів xi. Отримані в кожнім випробуванні значення вихідних параметрів накопичують, після N випробувань обробляють, що дає наступні результати: — гистограммы вихідних параметрів; — оцінки математичних очікувань і дисперсій вихідних параметрів: — оцінки коефіцієнтів кореляції й регресії між обраними вихідними й внутрішніми параметрами, які, зокрема, можна використати для оцінки коефіцієнтів чутливості.
Статистический аналіз, виконуваний відповідно до методу Монте-Карло, — трудомістка процедура, оскільки число випробувань N доводиться вибирати досить більшим, щоб досягти прийнятної точності аналізу. Інша причина, що утрудняє застосування методу Монте-Карло, — труднощі в одержанні достовірної вихідної інформації про закони розподілу параметрів-аргументів xi.
Більше
типова ситуація, коли закони розподілу
xi
невідомі,
але з
великою часткою
впевненості можна вказати гранично
припустимі відхилення
Δxi
параметрів
xi
від
номінальні значення xiном
(такі відхилення
часто вказуються в паспортних даних на
комплектуючі деталі). У таких випадках
більш реалистично
застосовувати метод аналізу на найгірший
випадок. Відповідно до цього методу,
спочатку виконують аналіз чутливості
з метою визначення знаків коефіцієнтів
чутливості. Далі здійснюють m
раз
одноваріантний аналіз, де m
-число
вихідних параметрів. У кожному варіанті
задають значення аргументів, найбільш
несприятливі для виконання умови
працездатності чергового вихідного
параметра
![]() .
Так, якщо yj<Tj
і
коефіцієнт чутливості позитивний
(тобто
.
Так, якщо yj<Tj
і
коефіцієнт чутливості позитивний
(тобто
![]() )
або yj>Tj
й
)
або yj>Tj
й
![]() ,
те
,
те
![]() інакше
інакше
![]() .
.
Однак варто помітити, що, проводячи аналіз на найгірший випадок, можна одержати завищені значення розкиду вихідних параметрів, і якщо домагатися виконання умов працездатності в найгірших випадках, те це часто веде до невиправданого збільшення вартості, габаритних розмірів, маси й інших показників проектованих конструкцій, хоча й гарантує із запасом виконання умов працездатності.
Організація
обчислювального процесу в універсальних
програмах аналізу на макрорівні. На
мал. 3.9 представлена графа-схема
обчислювального процесу при аналізі в
часовій
області
на макрорівні. Алгоритм відбиває
рішення
системи алгебро-дифференциальных
рівнянь
![]() На кожному кроці чисельного інтегрування
вирішується
система нелінійних алгебраїчних рівнянь
F(X)
= 0 методом Ньютона. На кожній ітерації
виконується рішення
системи лінійних алгебраїчних рівнянь
На кожному кроці чисельного інтегрування
вирішується
система нелінійних алгебраїчних рівнянь
F(X)
= 0 методом Ньютона. На кожній ітерації
виконується рішення
системи лінійних алгебраїчних рівнянь
![]() Інші
використовувані позначення:
Інші
використовувані позначення:
![]() —
початкові умови;
—
початкові умови;
![]() —
крок інтегрування і його початкове
значення;
—
крок інтегрування і його початкове
значення;
![]() —
вектор зовнішніх впливів;N
й
Nд
— число ньютоновских
ітерацій і його максимально припустиме
значення;ε — гранично припустима
погрішність рішення
СНАУ;
δ — погрішність, допущена на одному
кроці інтегрування; m1
— максимально припустиме значення
погрішності інтегрування на одному
кроці; m2
— нижня границя
коридору раціональних погрішностей
інтегрування.
—
вектор зовнішніх впливів;N
й
Nд
— число ньютоновских
ітерацій і його максимально припустиме
значення;ε — гранично припустима
погрішність рішення
СНАУ;
δ — погрішність, допущена на одному
кроці інтегрування; m1
— максимально припустиме значення
погрішності інтегрування на одному
кроці; m2
— нижня границя
коридору раціональних погрішностей
інтегрування.
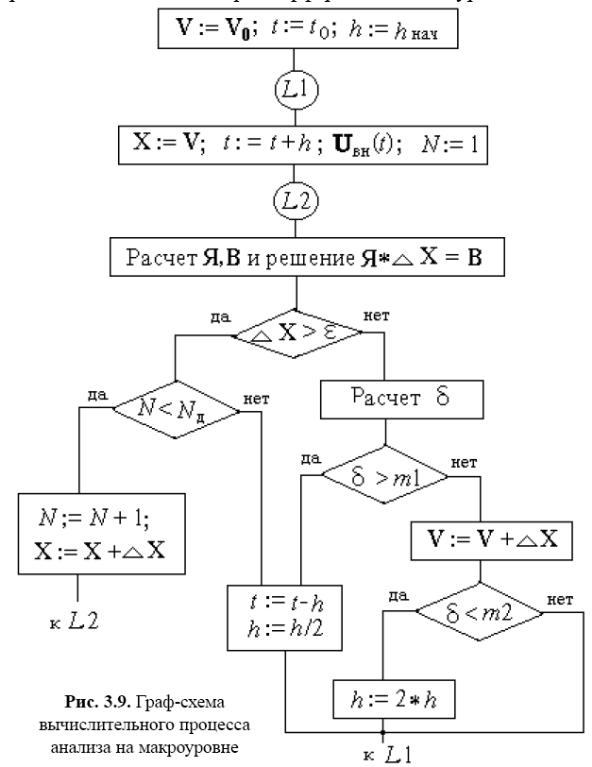 З малюнка
ясно, що при N
≥Nд
фіксується незбіжність ньютоновских
ітерацій і після дроблення кроку
відбувається повернення до інтегрування
при тих
же початкових для даного кроку умовах.
При збіжності розраховується і
залежно від того, виходить погрішність
за межі діапазону [m2,
m1]
чи ні крок змінюється або зберігає своє
колишнє значення.
З малюнка
ясно, що при N
≥Nд
фіксується незбіжність ньютоновских
ітерацій і після дроблення кроку
відбувається повернення до інтегрування
при тих
же початкових для даного кроку умовах.
При збіжності розраховується і
залежно від того, виходить погрішність
за межі діапазону [m2,
m1]
чи ні крок змінюється або зберігає своє
колишнє значення.
Параметры Nд, m1, m2, , hнач задаються “за замовчуванням” і можуть настроюватися користувачем.
Матрицю Якоби V і вектор правих частин ( необхідно розраховувати по програмі, що становить для кожного нового досліджуваного об'єкта. Складання програми виконує компілятор, що входить до складу програмного комплексу аналізу. Загальна структура такого комплексу представлена на мал. 3.10.
 Вихідні
дані про об'єкт можна задавати в графічному
виді
(у вигляді еквівалентної схеми) або
вхідною мовою програми аналізу. Запис
на такій мові
звичайно являє собою список компонентів
аналізованого об'єкта із вказівкою
їхніх взаємозв'язків. Дані, що вводять,
перетворяться у внутрішнє подання
за допомогою графічного й лінгвістичного
препроцесорів, у яких передбачена також
діагностика порушень формальних язикових
правил. Графічне подання
більш зручно, особливо для малодосвідчених
користувачів.
Вихідні
дані про об'єкт можна задавати в графічному
виді
(у вигляді еквівалентної схеми) або
вхідною мовою програми аналізу. Запис
на такій мові
звичайно являє собою список компонентів
аналізованого об'єкта із вказівкою
їхніх взаємозв'язків. Дані, що вводять,
перетворяться у внутрішнє подання
за допомогою графічного й лінгвістичного
препроцесорів, у яких передбачена також
діагностика порушень формальних язикових
правил. Графічне подання
більш зручно, особливо для малодосвідчених
користувачів.
Задавши опис об'єкта, користувач може приступитися до різноманітного аналізу або по одній із програм такого аналізу, або в інтерактивному режимі, змінюючи умови моделювання між варіантами за допомогою лінгвістичного препроцесора.
Найбільш складна частина комплексу — компілятор робочих програм, саме в ньому створюються програми розрахунку матриці Якоби V і вектора правих частин (, що фігурують в обчислювальному процесі (див. мал. 3.9). Властиво робоча програма (див. мал. 3.10) - це і є програма процесу, показаного на мал. 3.9. Для кожного нового моделируемого об'єкта складаються свої робочі програми. При компіляції використаються заздалегідь розроблені математичні моделі типових компонентів, відомі функції для відображення вхідних впливів і т.п. з відповідних бібліотек.
Постпроцессор представляє результати аналізу в табличній і графічній формах, це можуть бути залежності фазових змінних від часу, значення вихідних параметрів-функціоналів і т.п.
Процес аналізу на мікрорівні;
Математичні моделі на макрорівні. Математичними моделями на мікрорівні є диференціальні рівняння в частинних похідних або інтегральні рівняння, що описують поля фізичних величин. Інакше кажучи, на мікрорівні використаються моделі з розподіленими параметрами. У якості незалежних змінних у моделях можуть фігурувати просторові змінні x1, x2, x3 і час t.
Характерними прикладами моделей можуть служити рівняння математичної фізики разом із заданими крайовими умовами.
Наприклад:
1) рівняння теплопровідності
![]()
де : — питома теплоємність, ρ — щільність, ? — температура, t — час, λ — коефіцієнт теплопровідності, g — кількість теплоти, виділюваної в одиницю часу в одиниці об'єму;
2) рівняння дифузії
![]()
де N — концентрація часток, D — коефіцієнт дифузії;
3) рівняння безперервності, використовувані у фізику напівпровідникових приладів:
для дірок
![]()
для електронів
![]()
і рівняння Пуассона
![]()
Тут p й n — концентрації дірок й електронів; q — заряд електрона; Jp й Jn — щільності дырочного й електронного струмів; gp й gn — швидкості процесів генерації-рекомбінації дірок й електронів; & — напруженість електричного поля;, ρ - щільність електричного заряду; ? і ?0 - діелектрична проникність і діелектрична постійна.
Крайові умови включають початкові умови, що характеризують просторовий розподіл залежних змінних у початковий момент часу, і граничні, що задають значення цих змінних на границях розглянутої області у функції часу.
Методи аналізу на макрорівні. У САПР рішення диференціальних або інтегро-диференціальних рівнянь із частковими похідними виконується чисельними методами. Ці методи засновані на дискретизації незалежних змінних - їхньому поданні скінченою множиною значень в обраних вузлових точках досліджуваного простору. Ці точки розглядаються як вузли деякої сітки, тому використовувані в САПР методи - це сіткові методи.
Серед сіткових методів найбільше поширення одержали два методи: метод скінчених різниць (МКР) і метод скінчених елементів (МКЕ). Звичайно виконують дискретизацію просторових незалежних змінних, тобто використають просторову сітку. У цьому випадку результатом дискретизації є система звичайних диференціальних рівнянь для задачі нестаціонарної або система алгебраїчних рівнянь для стаціонарної.
Нехай необхідно вирішити рівняння
LV(z) = f(z)
с заданими крайовими умовами
MV(z) = ψ(z),
де L й M — диференціальні оператори, V(z) — фазова змінна, z = (x1, x2, x3, t) — вектор незалежних змінних, f(z) і ψ(z) — задані функції незалежних змінних.
У методі скінчених різниць алгебрування похідних по просторових координатах базується на апроксимації похідних кінцево-різницевими виразами. При використанні методу потрібно вибрати кроки сітки по кожній координаті та вид шаблона. Під шаблоном розуміють множина вузлових точок, значення змінних у які використаються для апроксимації похідної в одній конкретній точці.
Метод скінчених елементів базується на апроксимації не похідних, а самого рішення V(z). Але оскільки воно невідомо, то апроксимація виконується виразами з невизначеними коефіцієнтами qi
![]()
де QТ = (q1, q2,...qn)Т- вектор-рядок невизначених коефіцієнтів, ϕ(z) — вектор-стовпець координатних (опорних) функцій, заданих так, що задовольняються граничні умови.
При цьому мова йде про апроксимації рішення в межах кінцевих елементів, а з обліком їхніх малих розмірів можна говорити про використання порівняно простих апроксимуючих виразів U(z) (наприклад, ϕ(z) — поліноми низьких ступенів). У результаті підстановки U(z) у вихідне диференціальне рівняння й виконання операцій диференціювання одержуємо систему із якої потрібно знайти вектор Q.
![]() Цю
задачу
(визначення Q) вирішують
одним з наступних методів:
Цю
задачу
(визначення Q) вирішують
одним з наступних методів:
1) метод колокацій у якому, використовуючи (3.35), формують n рівнянь із невідомим вектором Q:
![]()
де n — число невизначених коефіцієнтів;
2) метод найменших квадратів заснований на мінімізації квадратів нев'язань (3.35) в n крапках або в середньому по розглянутій області;
3) метод Галеркіна за допомогою якого мінімізуються в середньому по області нев'язання з спеціально ваговими коефіцієнтами, що задають.
Найбільше поширення МКЕ одержав у САПР машинобудування для аналізу міцності об'єктів. Для цієї задачі можна використати розглянутий підхід, тобто виконати алгебраизацию вихідного рівняння пружності (рівняння Ламі).
Структура програм аналізу по МКЕ на мікрорівні. Основними частинами програми аналізу по МКЭ є бібліотеки кінцевих елементів, препроцесор, решатель і постпроцессор.
Бібліотеки кінцевих елементів (КЭ) містять моделі КЭ — їхньої матриці твердості. Очевидно, що моделі КЭ будуть різними для різних задач (аналіз пружних або пластичних деформацій, моделювання полів температур, електричних потенціалів і т.п.), різних форм КЭ (наприклад, у двовимірному випадку - трикутні або чотирикутні елементи), різних наборів координатних функцій.
Вихідні дані для препроцесора - геометрична модель об'єкта, найчастіше одержувана з підсистеми конструювання. Основна функція препроцесора - подання досліджуваного середовища (деталі) у сітковому виді, тобто у вигляді множини кінцевих елементів.
Решатель — програма, що ассемблирует (збирає) моделі окремих КЭ в загальну систему алгебраїчних рівнянь (3.41) і вирішує цю систему одним з методів розріджених матриць.
Постпроцессор служить для візуалізації результатів рішення в зручній для користувача формі. У машинобудівних САПР це графічна форма. Користувач може бачити вихідну (до нагружения) і деформовану форми деталі, поля напруг, температур, потенціалів і т.п. у вигляді кольорових зображень, у яких палітра кольорів або інтенсивність світіння характеризують значення фазової змінної.
Світовими лідерами серед програм кінцево-елементного аналізу є програмно-методичні комплекси Nastran, Ansys, Nisa, Adina, Cosmos.
Процес аналізу на функціонально-логічному рівні;
Моделювання і аналіз аналогових пристроїв. На функціонально-логічному рівні досліджують пристрою, як елементи яких приймають досить складні вузли і блоки, що вважалися системами на макрорівні. Тому необхідно спростити подання моделей цих вузлів і блоків у порівнянні з їхнім поданням на макрорівні. Інакше кажучи, замість повних моделей вузлів і блоків використовують їхні макромоделі.
Замість двох типів фазових змінних у моделях функціонально-логічного рівня фігурують змінні одного типу - сигнали. Фізичний зміст сигналу, тобто його віднесення до фазових змінним типу потоку або типу потенціалу, конкретизують у кожному випадку виходячи з особливостей задачі.
Основою моделювання аналогових пристроїв на функціонально-логічному рівні є використання апарата передаточних функцій. При цьому модель кожного елемента представляють у вигляді рівняння вхід-вихід, тобто у вигляді:
Vвих = f(Vвх), (3.42)
де Vвих й Vвх — сигнали на виході й вході вузла відповідно. Якщо вузол має більш ніж один вхід й один вихід, то в (3.42) скаляри Vвих й Vвх стають векторами.
Однак відомо, що подання моделі у вигляді (3.42) можливо тільки, якщо вузол є безінерційним, тобто в повній моделі вузла не фігурують похідні. Отже, для одержання (3.42) у загальному випадку потрібно попереднє алгебрування повної моделі. Таке алгебрування виконують за допомогою інтегральних перетворень, наприклад, за допомогою перетворення Лапласа, переходячи від часової області в простір комплексної змінної р. Тоді в моделях типу (3.42) мають місце не оригінали, а зображення сигналів Vвих(р) і Vвх(р), самі ж моделі реальних блоків намагаються по можливості спростити й представити їх як лінійну комбінацію типових блоків (ланок), які заздалегідь розробляються і включаються як бібліотечні моделі. Звичайно моделі ланок мають вигляд:
Vвих(р) = h(p)Vвх(р),
де h(p) — передаточна функція ланки.
У випадку застосування перетворення Лапласа з'являються обмеження на використання нелінійних моделей, а саме в моделях не повинне бути нелінійних інерційних елементів.
Інше допущення, що спрощує, при моделюванні на функціонально-логічному рівні - неврахування впливу навантаження на характеристики блоків. Дійсно, підключення до виходу блоку деякого іншого вузла ніяк не впливає на модель блоку (3.42).
Власне одержання ММС з ММЭ є, внаслідок прийнятих припущень, значно простіше, ніж на макрорівні: ММС є сукупність ММЭ, у яких ототожнені сигнали на з'єднаних входах і виходах елементів. Ця ММС представляє собою систему алгебраїчних рівнянь.
Одержання ММС проілюструємо простим прикладом (мал. 3.12), де показана система із трьох блоків з передаточними функціями h1(p), h2(p) і h3(p). ММС має вигляд:
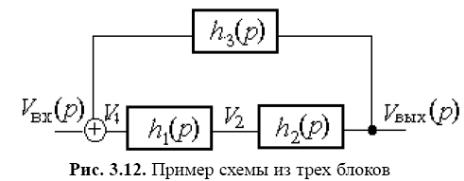
V2 = h1(p)V1;
Vвих(p) = h2(p)V2;
V1 = Vвх(p) + h3(p)Vвих(p)
або
Vвих(p) =H(p)Vвх(p),
де H(p) = h1(p) h2(p) / (1 - h1(p) h2(p) h3(p)).
Таким чином, аналіз зводиться до наступних операцій:
1) задану схему пристрою представляють сукупністю ланок й, якщо схема не повністю покривається типовими ланками, то розробляють оригінальні моделі;
2) формують ММС із моделей ланок;
3) застосовують пряме перетворення Лапласа до вхідних сигналів;
4) вирішують систему рівнянь ММС і знаходять зображення вихідних сигналів;
5) за допомогою зворотного перетворення Лапласа повертаються в тимчасову область із області комплексної змінної р.
Математичні моделі дискретних пристроїв. Аналіз дискретних пристроїв на функціонально-логічному рівні потрібно насамперед при проектуванні пристроїв обчислювальної техніки й цифрової автоматики. Тут додатково до припущень, прийнятих при аналізі аналогових пристроїв, використають дискретизацію сигналів, причому базовим є двозначне подання сигналів. Зручно цими двома можливими значеннями сигналів вважати “істина” (інакше 1) і “неправда” (інакше 0), а самі сигнали розглядати як логічні величини. Тоді для моделювання можна використати апарат математичної логіки. Необхідно відзначити, що бувають також три- і більше значні моделі.
Елементами цифрових пристроїв на функціонально-логічному рівні служать елементи, що виконують логічні функції, та функції зберігання інформації. Найпростішими елементами є диз’юнктор, кон’юнктор, інвертор, які реалізують відповідно операції диз'юнкції (АБО) y = a or b, кон’юнкції (І) y = a and b, заперечення (НЕ) y = not a, де y- вихідний сигнал, a й b — вхідні сигнали. Число входів може бути й більше двох. Умовні схемні позначення простих логічних елементів показані на рис. 3.13.

Математичні моделі пристроїв представляють собою систему математичних моделей елементів, що входять у пристрій.
Розрізняють синхронні й асинхронні моделі.
Синхронна модель представляє собою систему логічних рівнянь, у ній відсутній така змінна як час, синхронні моделі використають для аналізу уставлених режимів і станів.
Прикладом синхронної моделі може служити система рівнянь, отримана для логічної схеми тригера (мал. 3.14):
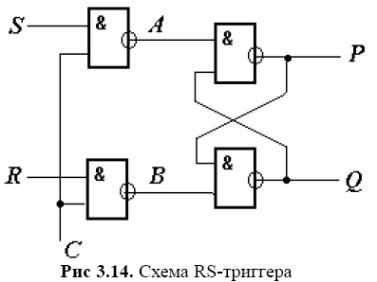
B = not (R and C); Q = not (B and P); P = not (A and Q);
A = not (S and C).
Асинхронні моделі відбивають не тільки логічні функції, але й часові затримки в поширенні сигналів. Асинхронна модель логічного елемента має вигляд
y(t+tзд) = f(X(t)), (3.43)
де tзд — затримка сигналу в елементі; f — логічна функція. Запис (3.43) означає, що вихідний сигнал y приймає значення логічної функції, що відповідає значенням аргументів X(t), у момент часу t+tзд. Отже, асинхронні моделі можна використати для аналізу динамічних процесів у логічних схемах.
Терміни синхронна й асинхронна моделі можна пояснити орієнтованістю цих моделей на синхронні й асинхронні схеми відповідно. У синхронних схемах передача сигналів між цифровими блоками відбувається тільки при подачі на спеціальні синхровходи тактових (синхронізуючих) імпульсів. Частота тактових імпульсів вибирається такою, щоб до моменту приходу синхроімпульсу перехідні процеси від попередніх передач сигналів фактично закінчилися. Отже, у синхронних схемах розрахунок затримок не актуальний, швидкодія пристрою визначається заданням тактової частоти.
Синхронні моделі можна використати не тільки для виявлення принципових помилок у схемній реалізації заданих функцій. З їхньою допомогою можна виявляти місця в схемах, небезпечні, з погляду, виникнення в них спотворень. Ситуації, пов'язані з потенційною небезпекою виникнення спотворень і збоїв, називають ризиками збою.
Розрізняють статичний і динамічний ризики збою.
Статичний ризик збою ілюструє ситуація рис. 3.15, якщо на два входи елемента И можуть приходити перепади сигналів у протилежних напрямках, як це показано на мал. 3.15,2. Якщо замість ідеального випадку, коли обидва перепади приходять у момент часу Т, перепади внаслідок розкиду затримок прийдуть неодночасно, причому так, як показано на мал. 3.15,б, то на виході елемента з'являється імпульс завади, який може спотворити роботу всього пристрою. Для усунення таких ризиків збою потрібно вміти їх виявляти. Із цією метою застосовують тризначне синхронне моделювання.

При цьому трьома можливими
значеннями сигналів є
0, 1 й
![]() ,
причому значення
інтерпретується як невизначеність.
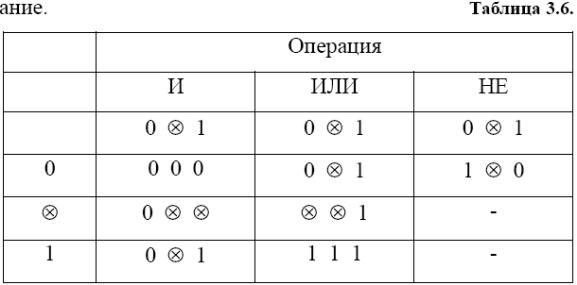
Правила виконання логічних операцій
И, АБО, НЕ в тризначному алфавіті очевидні
з розгляду табл. 3.6. У ній другий рядок
відведений для значень одного аргументу,
а перший стовпець
- для значень другого аргументу, значення
функцій представлені нижче другого
рядка і правіше
першого стовпця.
,
причому значення
інтерпретується як невизначеність.
Правила виконання логічних операцій
И, АБО, НЕ в тризначному алфавіті очевидні
з розгляду табл. 3.6. У ній другий рядок
відведений для значень одного аргументу,
а перший стовпець
- для значень другого аргументу, значення
функцій представлені нижче другого
рядка і правіше
першого стовпця.
При аналізі ризиків збою на кожному такті замість однократного рішення рівнянь моделі роблять дворазове рішення, тому можна говорити про вихідних, проміжних (після першого рішення) і підсумкових (після другого рішення) значеннях змінних. Для вхідних сигналів припустимі тільки такі послідовності вихідних, проміжних і підсумкових значень: 0-0-0, 1-1-1, 0- -1, 1- -0. Для інших змінних поява послідовності 0- -0 або 1- -1 означає невизначеність під час перехідного процесу, тобто можливість статичного ризику збою.
Для схеми рис. 3.15, результати тризначного моделювання представлені в табл. 3.7.

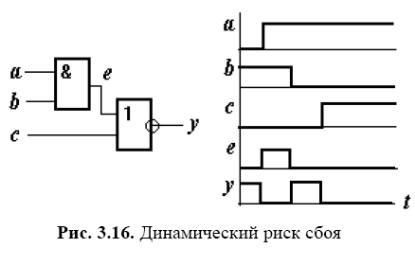
Динамічний ризик збою ілюструють схема і часові діаграми рис. 3.16. Збій виражається в появі замість одного перепаду на виході, що має місце при правильному функціонуванні, декількох перепадів. Виявлення динамічних ризиків збою також виконують за допомогою дворазового рішення рівнянь моделі, але при використанні п'ятизначного алфавіту із множиною значень {0, 1, , α, β}, де α інтерпретується як позитивний перепад, β — як негативний перепад, інші символи мають попереднє значення. Під час відсутності збоїв послідовності значень змінних у вихідному, проміжному й підсумковому станах можуть бути такими: 0-0-0, 1-1-1, 0-α-1, 1-β-0. Послідовності 0- -1 або 1- -0 вказують на динамічний ризик збою.
Тризначний алфавіт можна використати і в асинхронних моделях. Нехай у моделі y(t+tзд) = f(X(t)) у момент часу t1 входи X(t1) такі, що в момент часу t1+tзд відбувається перемикання вихідного сигналу y. Але якщо враховувати розкид затримок, то tзд приймає деяке випадкове значення в діапазоні [tзд min, tзд max] й, отже, у моделі в інтервалі часу від t1+tзд min до t1+tзд max сигнал y повинен мати невизначене значення Д. Саме це й досягається за допомогою тризначного асинхронного моделювання.
Методи логічного моделювання. Відносно асинхронних моделей можливі два методи моделювання - покроковий (інкрементний) і подієвий.
У покроковому методі час дискретизуються і обчислення по рівняннях моделі виконуються в дискретні моменти часу t0, t1, t2... і т.д. Крок дискретизації обмежений зверху значенням допустимої похибки визначення затримок і тому виявляється досить малим, а час аналізу значним.
Для скорочення часу аналізу використають подієвий метод. У цьому методі подією називають зміна будь-якої змінної моделі. Подієве моделювання базується на наступному правилі: звертання до моделі логічного елемента відбувається тільки в тому випадку, якщо на входах цього елемента відбулася подія. У складних логічних схемах на кожному такті синхронізації звичайно відбувається перемикання лише 2-3% логічних елементів й, відповідно, у подієвому методі в кілька разів зменшуються обчислювальні витрати в порівнянні з покроковим моделюванням.
Методи аналізу синхронних моделей являють собою методи вирішення систем логічних рівнянь. До цих методів відносяться метод ітерацій і метод Зейделя, які аналогічні однойменним методам рішення систем алгебраїчних рівнянь у неперервній математиці.
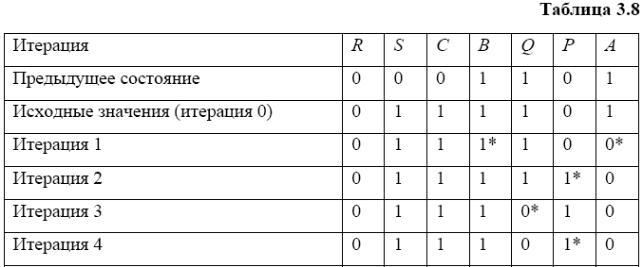
Застосування цих методів до моделювання логічних схем зручно проілюструвати на прикладі схеми тригера (див. рис. 3.14). У табл. 3.8 представлені значення змінні моделі у вихідному стані й після кожної ітерації відповідно до методу простих ітерацій. У вихідному стані задають початкові (часто довільні) значення проміжних і вихідному змінних, у даному прикладі це значення змінних B, Q, P, A, що відповідають попередньому стану тригера. Новий стан тригера повинне відповідати зазначеним у таблиці зміненим значенням вхідних сигналів R, S й C. Обчислення закінчуються, якщо на черговій ітерації нема змін змінних, що й спостерігається в даному прикладі на четвертій ітерації.
Відповідно до методу простих ітерацій, у праві частини рівнянь моделі на кожній ітерації підставляють значення змінних, отримані на попередній ітерації. На відміну від цього в методі Зейделя, якщо в деякої змінної обновлене значення на поточній ітерації, те саме його й використають у подальших обчисленнях уже на поточній ітерації. Метод Зейделя дозволяє скоротити число ітерацій, але для цього потрібно попередньо впорядкувати рівняння моделі так, щоб послідовність обчислень відповідала послідовності проходження сигналів по схемі.
Таке впорядкування виконують за допомогою ранжування.
Ранжування полягає в присвоєнні елементам і змінним моделі значень рангів у відповідності з наступними правилами:
1) у схемі розриваються всі контури зворотного зв'язку, що приводить до появи додаткових входів схеми (псевдовходів);
2) всі зовнішні змінні (у тому числі на псевдовходах) одержують ранг 0;
3) елемент і його вихідні змінні одержують ранг k, якщо в елемента всі входи проранжовані і старший серед рангів входів дорівнює k-1.
Так, якщо в схемі (див. рис. 3.14) розірвати наявний контур зворотного зв'язку в колі змінної Q і позначити змінну на псевдовході Q1, то ранги змінних виявляться наступними: R, S, C, Q1 мають ранг 0, K й I — ранг 1, S — ранг 2 й Q — ранг 3. Відповідно до цього з рівняння в моделі тригера:
A = not (S and C). B = not (R and C); P = not (A and Q); Q = not (B and P).
Тепер уже на першій ітерації по Зейделю одержуємо необхідний результат. Якщо розірвати контур зворотного зв'язку в колі змінної P, то рішення в даному прикладі буде отримано після другої ітерації, але це однаково швидше, ніж при використанні методу простої ітерації.
Для скорочення об'єму обчислень у синхронному моделюванні можливе використання подієвого підходу. Як і раніше звертання до моделі елемента відбувається, тільки якщо на його входах відбулася подія.
Для тригера (див. рис. 3.14) застосування подієвості в рамках методу простих ітерацій приводить до скорочення об'єму обчислень: замість 16-кратних звертань до моделей елементів, як це видно з табл. 3.8, відбувається лише 5-кратний обіг. У табл. 3.8 зірочками позначені значення змінних, що обчислюють у подієвому методі. Так, наприклад, на ітерації 0 мають місце зміни змінних S й C, тому на наступній ітерації обігу відбуваються тільки до моделей елементів з виходами K й I.
Процес аналізу на системному рівні;
Основні відомості з теорії масового обслуговування.
Об'єктами проектування на системному рівні є такі складні системи, як виробничі підприємства, транспортні системи, обчислювальні системи й мережі, автоматизовані системи проектування й керування й т.п. У цих випадках аналіз процесів функціонування систем пов'язаний з дослідженням проходження через систему потоку заявок (інакше називаних запитами або транзакціями). Розроблювачів подібних складних систем цікавлять насамперед такі параметри, як продуктивність (пропускна здатність) проектованої системи, тривалість обслуговування (затримки) заявок у системі, ефективність використовуваного в системі обладнання.
Заявками можуть бути замовлення на виробництво виробів, задачі, розв'язувані в обчислювальній системі, клієнти в банках, вантажі, що надходять на транспортування й ін. Очевидно, що параметри заявок, що надходять у систему, є випадковими величинами і при проектуванні можуть бути відомі лише їхні закони розподілу і числові параметри цих розподілів. Тому аналіз функціонування на системному рівні, як правило, носить статистичний характер. Як математичний апарат моделювання зручно використовувати теорію масового обслуговування, а як моделі систем на цьому рівні використати системи масового обслуговування (СМО).
Типовими вихідними параметрами в СМО є числові характеристики таких величин, як:
- час обслуговування заявок у системі,
- довжини черг заявок на входах,
- час очікування обслуговування в чергах,
- завантаження пристроїв системи,
- імовірність обслуговування в заданий термін і т.п.
У найпростішому випадку СМО являє собою деякий засіб (пристрій) - обслуговуючий апарат (ОА), разом із чергами заявок на входах. Складніші СМО складаються з багатьох взаємозалежних ОА, які в сукупності утворять статичні об'єкти СМО - ресурси. Наприклад, в обчислювальних мережах ресурси представлені апаратними й програмними засобами.
У СМО, крім статичних об'єктів, фігурують динамічні об'єкти — транзакти. Наприклад, в обчислювальних мережах динамічними об'єктами є розв'язувані задачі й запити на інформаційні послуги.
Стан СМО характеризується станами складових її об'єктів. Наприклад, стани ОА виражаються логічними величинами, значення яких інтерпретуються як true (зайняте) і false (вільно), і довжинами черг на входах ОА, що приймають позитивні цілі значення. Змінні, які характеризують стан СМО називають змінними стану або фазовими змінними.
Правило, відповідно до якого заявки вибирають із черг на обслуговування, називають дисципліною обслуговування, а величину, що виражає переважне право на обслуговування, - пріоритетом.
У безпріоритетних дисциплінах, всі транзакти мають однакові пріоритети. Серед безпріоритетних дисциплін найбільш популярні дисципліни FIFO (першим прийшов - першим обслужений), LIFO (останнім прийшов - першим обслужений) і з випадковим вибором заявок з черг.
У пріоритетних дисциплінах, для заявок кожного пріоритету на вході ОА виділяється своя черга. Заявка із черги з низьким пріоритетом надходить на обслуговування, якщо порожні черги з вищими пріоритетами. Розрізняють пріоритети абсолютні, відносні й динамічні.
Заявка із черги з вищим абсолютним пріоритетом, надходячи на вхід зайнятого ОА, перериває вже почате обслуговування заявки нижчого пріоритету. У випадку відносного пріоритету переривання не відбувається, заявка з вищим пріоритетом чекає закінчення вже початого обслуговування. Динамічні пріоритети можуть змінюватися під час знаходження заявки в СМО.
Дослідження поводження СМО (визначення часових залежностей змінних, які характеризують стан СМО) при подачі на входи потоків заявок (відповідно до завдання на експеримент), називають імітаційним моделюванням СМО. Імітаційне моделювання проводять шляхом відтворення подій, що відбуваються одночасно або послідовно в часі.
Підхід, альтернативний імітаційному моделюванню, називають аналітичним дослідженням СМО, яке полягає в одержанні аналітичних виразів для розрахунку вихідних параметрів СМО з наступною підстановкою значень аргументів у ці вирази в кожному окремому експерименті.
Моделі СМО, які використовуються при імітаційному й аналітичному моделюванні, називаються імітаційними й аналітичними відповідно.
Аналітичні моделі зручні у використанні, оскільки для аналітичного моделювання не потрібні значні витрати обчислювальних ресурсів, часто без постановки спеціальних обчислювальних експериментів розроблювач може оцінити характер впливу аргументів на вихідні параметри, виявити ті або інші загальні закономірності в поведінці системи. Але, на жаль, аналітичне дослідження вдається реалізувати тільки для порівняно нескладних СМО. Для складних СМО аналітичні моделі якщо й вдається одержати, то тільки при прийнятті допущень, які спрощують систему, що ставлять під сумнів адекватність моделі.
Тому основним підходом до аналізу САПР на системному рівні проектування вважають імітаційне моделювання, а аналітичне дослідження використають при попередній оцінці різних варіантів систем.
Деякі компоненти СМО характеризуються більш ніж одним вхідним та (або) вихідним потоками заявок. Правила вибору одного з можливих напрямків руху заявок входять у відповідні моделі компонентів. В одних випадках такі правила ставляться до вихідних даних (наприклад, вибір напрямку по ймовірності), але в деяких випадках бажано знайти оптимальне керування потоками у вузлах розгалуження. Тоді задача моделювання стає складнішою задачею синтезу, характерними прикладами є маршрутизація заявок або синтез розкладів і планів.
Аналітичні моделі СМО. Як відзначено вище, аналітичні моделі СМО вдається одержати при досить серйозних припущеннях. До числа типових припущень відносяться наступні.
як правило, вважають, що в СМО використаються безпріоритетні дисципліни обслуговування типу FIFO;
часи обслуговування заявок у пристроях вибираються відповідно до експонентного закону розподілу;
в аналітичних моделях СМО вхідні потоки заявок апроксимуються найпростішими потоками, тобто потоками, що володіють властивостями стаціонарності та ординарності (неможливості одночасного надходження двох заявок на вхід СМО) та відсутності післядії.
У більшості випадків моделі СМО відображають процеси з кінцевою множиною станів і з відсутністю післядії. Такі процеси називають кінцевими марковськими колами.
Марковські кола характеризуються множиною станів S, матрицею ймовірностей переходів з одного стану в інший й початковими умовами (початковим станом). Зручно представляти марковське коло у вигляді графа, в якому вершини відповідають станам кола, дуги - переходам, ваги дуг - імовірностям переходів (для дискретного часу) або інтенсивностям переходів (для неперервного часу).
Інтенсивністю переходу називають величину Vij = lim Pij(t1) / t1 при t1→0, де Pij(t1) — імовірність переходу зі стану Si у стан Sj за час t1. Звичайно приймається умова

де N — число станів. На рис. 3.17 наведений приклад Маяковського кола у вигляді графа зі станами S1,...,S4, а в табл. 3.9 представлена матриця інтенсивностей переходів для цього прикладу.

Більшість вихідних параметрів СМО можна визначити, використовуючи інформацію про поведінку СМО, тобто інформацію про стани СМО в стаціонарних режимах і про їхні зміни в перехідних процесах. Ця інформація має імовірнісну природу, яка обумовлює опис поведінки СМО в термінах імовірностей знаходження системи в різних станах. Основою такого опису, а отже, і багатьох аналітичних моделей СМО є рівняння Колмогорова.
Рівняння Колмогорова можна одержати в такий спосіб.
Зміна ймовірності Pi знаходження системи в стані Si за час t1 є імовірність переходу системи в стан Si з будь-яких інших станів за винятком імовірності переходу зі стану Si в інші стани за час t1, тобто
![]()
де Pi(t) і Pj(t) — імовірності знаходження системи в станах Si й Sj відповідно в момент часу t, а Pji(t1) і Pik(t1) — імовірності зміни станів протягом часу t1; добуток виду Pji(t1)Pj(t) є безумовна ймовірність переходу з Sj в Si, рівна умовної ймовірності переходу, помноженої на ймовірність умови; J і K — множини індексів вершин стосовно вершини Si по вхідних і вихідних дугах на графі станів відповідно.
Розділивши
(3.45) на t1
і перейшовши до межі при t→0,
одержимо

Приклад аналітичної моделі.
Прикладом СМО,
до якої можна застосувати
аналітичні методи дослідження, є
одноканальна СМО
з
найпростішим вхідним потоком інтенсивністю
![]() і
тривалістю обслуговування, що підкоряється
експонентному закону
обслуговування інтенсивністю
і
тривалістю обслуговування, що підкоряється
експонентному закону
обслуговування інтенсивністю
![]() .
Для цієї
СМО
потрібно одержати
аналітичні залежності середнього числа
Nav
заявок, що перебувають
у системі, середню довжину
.
Для цієї
СМО
потрібно одержати
аналітичні залежності середнього числа
Nav
заявок, що перебувають
у системі, середню довжину
![]() черги до ОА,
час
черги до ОА,
час
![]() перебування заявки в системі, час
перебування заявки в системі, час
![]() очікування
в черзі.
очікування
в черзі.
На мал. 3.18 представлений граф станів розглянутої СМО, де Sk — стан з k заявками в системі. Матриця інтенсивностей представлена в табл. 3.10. Рівняння Колмогорова для сталого режиму мають вигляд



Імітаційне моделювання СМО. Для подання імітаційних моделей можна використати мови програмування загального призначення, однак такі подання виявляються досить громіздкими. Тому звичайно застосовують спеціальні мови імітаційного моделювання на системному рівні. Серед мов імітаційного моделювання розрізняють мови, орієнтовані на опис подій, засобів обслуговування або маршрутів руху заявок (процесів).
Вибір мови моделювання визначає структуру моделі й методику її побудови.
Орієнтація на пристрої характерна для функціонально-логічного й детальніших ієрархічних рівнів опису об'єктів.
Для опису імітаційних моделей на системному рівні частіше використають мови, орієнтовані на події або процеси. Прикладами перших можуть служити мови Сімскріпт і SMPL. Прикладами других можуть бути мови Симула, SOL та GPSS.
Мови імітаційного моделювання реалізуються в програмно-методичних комплексах моделювання СМО, які мають той або інший ступінь спеціалізації. Так, комплекси на базі мови GPSS можна використати в багатьох додатках, але є спеціалізовані комплекси для моделювання обчислювальних мереж, систем керування підприємствами й т.п.
При використанні мов, орієнтованих на процеси, у складі моделі виділяються елементарні частини й ними можуть бути джерела вхідних потоків заявок, пристрою, накопичувачі й вузли.
Джерело вхідного потоку заявок являє собою алгоритм, відповідно до якого обчислюються моменти tk появи заявок на виході джерела. Джерела можуть бути залежними й незалежними. У залежних джерелах моменти появи заявок пов'язані з настанням певних подій, наприклад, із приходом іншої заявки на вхід деякого пристрою. Типовим незалежним джерелом є алгоритм вироблення значень випадкової величини із заданим законом розподілу.
Пристрої в імітаційній моделі представлені алгоритмами генерації значень інтервалів (тривалості) обслуговування. Найчастіше це алгоритми генерації значень випадкових величин із заданим законом розподілу. Але можуть бути пристрої з детермінованим часом обслуговування або часом, обумовленим подіями в інших частинах моделі.
Накопичувачі моделюються алгоритмами визначення об'ємів пам'яті, займаних заявками, що приходять на вхід накопичувача. Звичайно об'єм пам'яті, займаний заявкою, обчислюється як значення випадкової величини, закон й (або) числові характеристики розподілу може залежати від типу заявки.
Вузли. виконують сполучні, керуючі й допоміжні функції в імітаційній моделі, наприклад, для вибору напрямків руху заявок, зміни їхніх параметрів і пріоритету, поділу заявок на частині, їхнього об'єднання й т.п.
Звичайно кожному типу елементарної моделі, за винятком лише деяких вузлів, у програмній системі відповідає певна процедура (підпрограма). Тоді модель можна представити як алгоритм, що складається з упорядкованих звертань до цих процедур, що відбивають поводження модельованої системи.
У процесі моделювання відбуваються зміни модельованого часу, що найчастіше приймається дискретним, вимірюваним у тактах. Час змінюється після того, як закінчена імітація чергової групи подій, які відносяться до моменту часу tk. Імітація супроводжується нагромадженням статистики таких даних, як кількості заявок, що вийшли із системи обслуженими і необслуженими, сумарний час зайнятого стану для кожного із пристроїв, середні довжини черг і т.п. Імітація закінчується, коли поточний час перевищить заданий відрізок часу або коли вхідні джерела вироблять задане число заявок. Після цього роблять обробку накопичених у файлі статистики даних, що дозволяє одержати значення необхідних вихідних параметрів.
Подієвий метод моделювання. У програмах імітаційного моделювання СМО переважно реалізується подієвий метод організації обчислень. Сутність цього методу полягає у відстеженні на моделі послідовності подій у тім же порядку, у якому вони відбувалися б у реальній системі. Обчислення виконують тільки для тих моментів часу й тих частин моделі, до яких відносяться вчинені події. Інакше кажучи, обіг на черговому такті модельованого часу здійснюються тільки для моделей тих елементів (пристроїв, накопичувачів), на входах яких у цьому такті відбулися зміни. Оскільки зміни станів у кожному такті звичайно спостерігаються лише в малій частині ОА, подієвий метод може істотно прискорити моделювання в порівнянні з інкрементним методом, у якому на кожному такті аналізуються стани всіх елементів моделі.
Розглянемо можливу схему реалізації подієвого методу імітаційного моделювання.
Моделювання починається з перегляду операторів генерування заявок, тобто зі звертання до моделей джерел вхідних потоків. Для кожного незалежного джерела такий обіг дозволяє розрахувати момент генерації першої заявки. Цей момент разом з ім'ям - посиланням на заявку - заноситься в список майбутніх подій (СБС), а відомості про заявку - у список заявок (СЗ).
Запис у СЗ містить у собі ім'я заявки, значення її параметрів (атрибутів), місце, займане в цей момент у моделі. У СБС події впорядковуються по збільшенню моментів настання.
Потім з СБС вибирають сукупність відомостей про події, що ставляться до найбільш раннього моменту часу. Ця сукупність переноситься в список поточних подій (СТС), з якого витягаються посилання на події. Обіг по посиланню до СЗ дозволяє встановити місце в моделі заявки А, з якої зв'язане модельована подія. Нехай цим місцем є пристрій Х. Далі програма моделювання виконує наступні дії (рис. 3.19):
1) змінює параметри стану пристрою Х, наприклад, якщо заявка А звільняє Х, а черга до Х не була порожня, то відповідно до заданої дисципліни обслуговування із черги до Х вибирається заявка В и надходить на обслуговування в Х;
2) прогнозується час настання наступної події, пов'язаного із заявкою В, шляхом звертання до моделі пристрою Х, у якій розраховується тривалість обслуговування заявки В; відомості про цю майбутню подію заносяться в СБС і СЗ;
3) відбувається імітація руху заявки А в моделі по маршруті, обумовленому заданою програмою моделювання, доти, поки заявка не прийде на вхід деякого ОА; тут або заявка затримується в черзі, або шляхом звертання до моделі цього ОА прогнозується настання деякої майбутньої події, пов'язаної з подальшою долею заявки А; відомості про цю майбутню подію також заносяться в СБС і СЗ;
4) у файл статистики додаються необхідні дані.
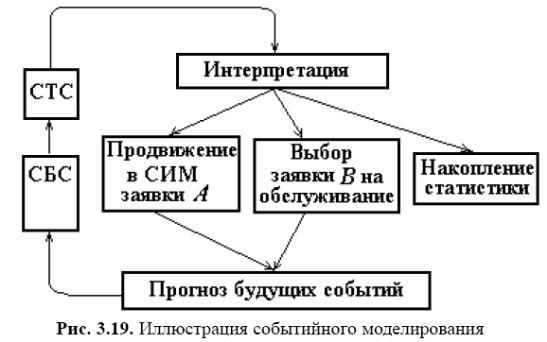
Після відпрацьовування всіх подій, що відносяться до моменту часу tk, відбувається збільшення модельного часу до значення, що відповідає найближчому майбутньому події, і розглянутий процес імітації повторюється.
Мережі Петрі — апарат для моделювання динамічних дискретних систем (переважно асинхронних паралельних процесів). Мережа Петрі визначається як четвірка <P,T,I,O>, де Р и M — кінцеві множини позицій і переходів, I й 0 — множини вхідних і вихідних функцій. Інакше кажучи, мережа Петрі являє собою орієнтований граф, у якому позиціям відповідають вершини, зображувані кружками, а переходам — вершини, зображувані стовщеними рисками; функціям I відповідають дуги, спрямовані від позицій до переходів, а функціям ПРО — від переходів до позицій.
Як і у системах масового обслуговування, у мережах Петрі вводяться об'єкти двох типів: динамічні — зображуються мітками (маркерами) усередині позицій і статичні — їм відповідають вершини мережі Петрі.
Розподіл маркерів по позиціях називають маркуванням. Маркери можуть переміщатися в мережі. Кожна зміна маркування називають подією, причому кожна подія пов'язане з певним переходом. Уважається, що події відбуваються миттєво й різночасно при виконанні деяких умов Кожній умові в мережі Петрі відповідає певна позиція. Здійсненню події відповідає спрацьовування (порушення або запуск) переходу, при якому маркери із вхідних позицій цього переходу переміщаються у вихідні позиції. Послідовність подій утворить моделируемый процес.
Правила спрацьовування переходів (рис. 3.21), конкретизують у такий спосіб: перехід спрацьовує, якщо для кожної з його вхідних позицій виконується умова Ni Ki, де Ni — число маркерів в i-й вхідній позиції, Ki — число дуг, що йдуть від i-й позиції до переходу; при спрацьовуванні переходу число маркерів в i-й вхідної позиції зменшується на Ki, а в j-й вихідної позиції збільшується на Mj, де Mj — число дуг, єднальний перехід з j-й позицією.
На рис. 3.21 показаний приклад розподілу маркерів по позиціях перед спрацьовуванням, це маркування записують у вигляді (2,2,3,1). Після спрацьовування переходу маркування стає іншою:
(1,0,1,4).
Можна вводити ряд додаткових правил й умов в алгоритми моделювання, одержуючи той або інший різновид мереж Петрі. Так, насамперед корисно ввести модельний час, щоб моделювати не тільки послідовність подій, але і їхню часову прив'язку. Це здійснюється доданням переходам ваги - тривалості (затримки) спрацьовування, яку можна визначати, використовуючи алгоритм, що задає при цьому. Отриману модель називають часовою мережею Петрі.
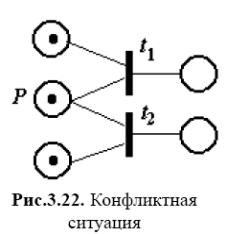
Якщо затримки є випадковими величинами, то мережу називають стохастичною. У стохастичних мережах можливе введення ймовірностей спрацьовування збуджених переходів. Так, на рис. 3.22 представлений фрагмент мережі Петрі, що ілюструє конфліктну ситуацію — маркер у позиції p може запустити або перехід t1, або перехід t2. У стохастичній мережі передбачається імовірнісний вибір переходу, що спрацьовує, у таких ситуаціях.
Якщо затримки визначаються як функції деяких аргументів, якими можуть бути кількості маркерів у яких-небудь позиціях, стану деяких переходів і т.п., то мережу називають функціональною.
У багатьох задачах динамічні об'єкти можуть бути декількох типів, і для кожного типу потрібно вводити свої алгоритми поводження в мережі. У цьому випадку кожен маркер повинен мати хоча б один параметр, що позначає тип маркера. Такий параметр звичайно називають кольорами; кольори можна використати як аргумент у функціональних мережах. Мережа Петрі при цьому називають кольоровий.
Серед інших різновидів мереж Петрі варто згадати інгібіторні мережі, які характеризуються тим, що в них можливі заборонні (ингибиторные) дуги. Наявність маркера у вхідній позиції, пов'язаної з переходом ингибиторной дугою, означає заборона спрацьовування переходу.
Введені поняття пояснимо на наступному прикладі.
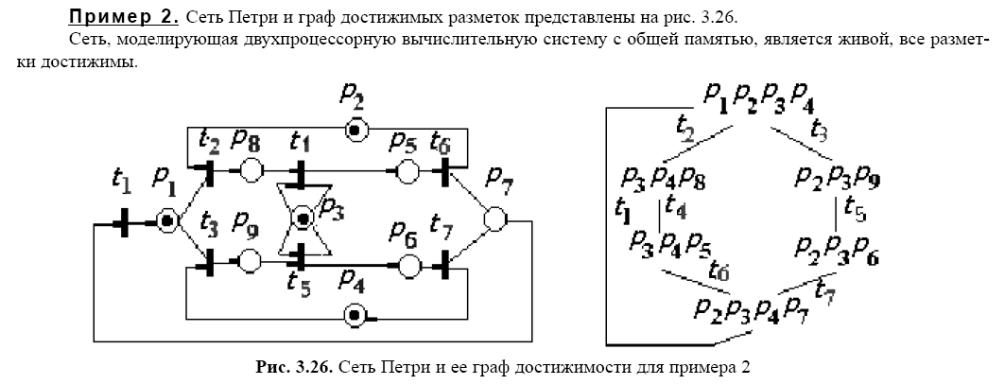
Приклад. Потрібно описати за допомогою мережі Петрі роботу групи користувачів на єдиній робочій станції WS при заданих характеристиках потоку запитів на користування WS і характеристиках вступників задач.
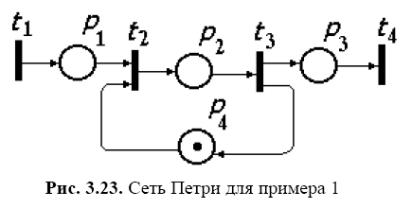
Мережа Петрі представлена на мал. 3.23.
Тут переходи зв'язані з наступними подіями: t1 — надходження запиту на використання WS, t2 — заняття станції, t3 — звільнення станції, t4 — вихід обслуженої заявки; позиція "4 використається для відображення стану WS: якщо в "4 є мітка, то WS вільна й заявка, що прийшла, викликає спрацьовування переходу t2; поки ця заявка не буде обслужена, мітки в "4 не буде, отже, що прийшли у позицію "1 запити змушені очікувати спрацьовування переходу t3.

Аналіз Мереж Петрі. Аналіз складних систем на базі мереж Петрі можна виконувати за допомогою імітаційного моделювання СМО, представлених моделями мереж Петрі. При цьому задають вхідні потоки заявок і визначають відповідну реакцію системи. Вихідні параметри СМО розраховують шляхом обробки накопиченого при моделюванні статистичного матеріалу.
Можливий й інший підхід до використання мереж Петрі для аналізу об'єктів, досліджуваних на системному рівні. Він не пов'язаний з імітацією процесів і заснований на дослідженні таких властивостей мереж Петрі, як обмеженість, безпека, сохраняемость, досяжність, жвавість.
Обмеженість (або До-обмеженість) має місце, якщо число міток у будь-якій позиції мережі не може перевищити значення К. При проектуванні автоматизованих систем визначення До дозволяє обґрунтовано вибирати ємності накопичувачів. Можливість необмеженого росту числа міток свідчить про небезпеці необмеженого росту довжин черг.
Безпека — окремий випадок обмеженості, а саме це 1-обмеженість. Якщо для деякої позиції встановлено, що вона безпечна, то її можна представляти одним тригером.
Сохраняемость характеризується сталістю завантаження ресурсів, тобто

де Ni-число маркерів в i-й позиції, Ai — вагарні коефіцієнт.
Досяжність Mk → Mj характеризується можливістю досягнення маркування Mj зі стану мережі, характеризуемого маркуванням Mk.
Жвавість мережі Петрі визначається можливістю спрацьовування будь-якого переходу при функціонуванні модельованого об'єкта. Відсутність жвавості означає або надмірність апаратур у проектованій системі, або свідчить про можливості виникнення зациклень, тупиків, блокувань.
В основі дослідження перерахованих властивостей мереж Петрі лежить аналіз досяжності.
Один з методів аналізу досяжності будь-якого маркування зі стану Eо — побудова графа досяжності. Початкова вершина графа відображає Eо, а інші вершини відповідають маркуванням. Дуга з Ei в Ej означає подію Mi → Mj і відповідає спрацьовуванню переходу t.
У складних мережах граф може містити надмірно велика кількість вершин і дуг. Однак при побудові графа можна не відображати всі вершини, тому що багато хто з них є дублями (дійсно, від маркування Mk завжди породжується той самий подграф поза залежністю від того. з якого стану система прийшла в Ek). Тупики виявляються по відсутності дозволених переходів з якої-небудь вершини, тобто по наявності листів - термінальних вершин. Необмежений ріст числа маркерів у якій-небудь позиції свідчить про порушення обмеженості.
Приведем приклади аналізу досяжності.
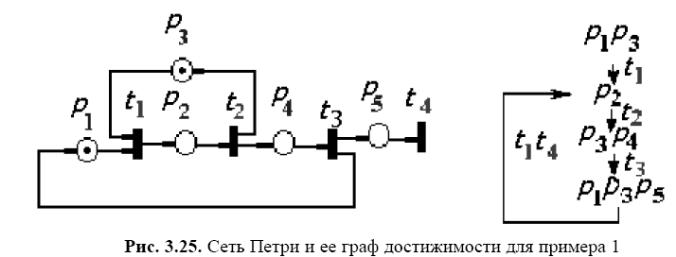
Приклад 1. Мережа Петрі й граф досяжних розміток представлені на мал. 3.25.
На малюнку вершини графа зображені у вигляді маркувань, дуги позначені переходами, що спрацьовують. Жвавість мережі очевидна, тому що спрацьовують всі переходи, тупики відсутні.