§4. Применения операционного исчисления

Операционное исчисление (преобразование Лапласа) чаще всего применяется к решению линейных дифференциальных уравнений с постоянными коэффициентами (задачи Коши)

(1)

с начальными условиями

(1')

Пусть и неизвестная функция вместе со своими производными являются оригиналами. Тогда

Найдем изображение уравнения (1)

или

(2)

где характеристический многочлен уравнения (1). Как видно, вместо задачи (1), (1') получили алгебраическое уравнение (2). Разрешая его, найдем изображение неизвестной функции

(3)

Осталось по известному изображению найти оригинал и задача будет решена.

Если изображение (3) является дробно рациональной

функцией, причем то ее можно разложить на простейшие дроби

(4)

Поскольку то оригиналом (4) будет (5)

Пример 1. Решить уравнение с нулевыми начальными условиями.

Решение. В нашем случае

Найдем корни знаменателя и разложим рациональную дробь на простейшие дроби.

Коэффициенты находятся обычным способом

Используя (5), получим

Пример 2. Решить задачу Коши:

Решение. Пусть тогда Используя теорему умножения, найдем

Очевидно, изображением нормальной СЛДУ с постоянными коэффициентами и начальным условием является СЛАУ Если она имеет единственное решение, то его можно записать так:

Здесь единичная матрица. Осталось по известному изображению найти оригинал и система дифференциальных уравнений будет решена.

Порядок некоторых дифференциальных уравнений можно понизить, если найти их изображение по Лапласу.

Пример 3. Решить уравнение

Решение. Пусть тогда

Согласно свойству дифференцирования изображения, найдем

изображение данного дифференциального уравнения. Получили дифференциальное уравнение первого порядка с разделяющимися переменными.

(см. пример 2 §3). Итак, решение данного уравнения.

Дифференциальное уравнение вида

(6)

где старшая производная неизвестной функции зависит от аргумента а младшие от аргумента со сдвигом называется дифференциальным уравнением с запаздывающим аргументом. Такое уравнение также можно решать операционным методом.

Пример 4. Решить уравнение

(7)

Решение. Найдем изображение уравнения.

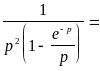
Используя первую теорему разложения и свойство запаздывания оригинала, запишем решение данного уравнения в виде

Операционным методом можно решать интегральные уравнения типа свертки

Здесь известные функции, а искомая функция.

Пример 5. Решить уравнение

Решение. Найдем изображение уравнения.

Итак, решение данного уравнения. Уравнения математической физики также можно решать операционным методом.

Пример 6. Концы струны x = 0 и закреплены жестко. Начальное отклонение задано уравнением Начальная скорость равна нулю. Найти отклонения струны при

Решение. Отклонения струны определяются волновым уравнением

(8)

граничными условиями

(9)

и начальными условиями

(10)

Пусть тогда вместо (8) с учетом начальных условий (10) получим

(11)

Уравнение (11) - обыкновенное дифференциальное уравнение с постоянными коэффициентами, удовлетворяющее следующим граничным условиям

(9')

Решение уравнения (11) с граничными условиями (9') следующее:

Тогда, очевидно, решение данной задачи.

70