Тема 3. Основы аналитической геометрии

Предмет аналитической геометрии. Прямая на плоскости.

Общее уравнение прямой. Уравнение прямой с угловым коэффициентом.

Взаимное расположение двух прямых на плоскости: угол между двумя прямыми, условие параллельности и перпендикулярности прямых, расстояние от точки до прямой.

Общее уравнение плоскости в пространстве. Частные случаи. Уравнение плоскости, проходящей через три заданные точки. Уравнение плоскости в отрезках.

Взаимное расположение двух плоскостей: параллельность, перпендикулярность. Расстояние от точки до плоскости.

Уравнения прямой на плоскости.

Прямая в пространстве. Канонические уравнения прямой в пространстве. Прямая как линия пересечения двух плоскостей. Уравнение прямой, проходящей через две заданные точки.

Взаимное расположение прямых, прямой и плоскости в пространстве.

Линии второго порядка: окружность, эллипс, гипербола, парабола.

Геометрический смысл систем уравнений и систем неравенств с двумя и тремя переменными.

Квадратичные формы. Матричная форма записи. Основные свойства.

Правила выполнения и оформления контрольной работы

В первом учебном семестре все студенты-заочники выполняют контрольную работу по первому разделу дисциплины “Высшая математика” – “Элементы линейной и векторной алгебры. Аналитическая геометрия”. Контрольная работа включает в себя 4 задачи по соответствующим темам дисциплины.

К решению каждой задачи следует приступать только после изучения теоретического материала определенной темы.

При выполнении контрольной работы необходимо строго придерживаться нижеуказанных правил:

1. Контрольная работа должна быть представлена в отдельной тетради.

Образец оформления титульного листа контрольной работы приведен в приложении 1.

2. Решение задач следует располагать в порядке возрастания их номеров, дополнительно указывая в скобках номер варианта. Перед решением каждой задачи необходимо полностью написать ее условие, заменить буквенные обозначения числовыми данными соответствующего варианта. Выбор вариантов осуществляется в соответствии с номером, под которым в учебном журнале записан студент.

3. Решение всех задач должно быть снабжено подробными пояснениями. При необходимости следует сделать ссылки на соответствующие положения теории с указанием теорем, формул, использованных при решении задачи. Все вычисления, в том числе и промежуточные, вспомогательные, приводить полностью, рационально округлив результаты.

4. Рисунки, чертежи выполнить аккуратно и четко в удобном масштабе и пронумеровать. Все обозначения на рисунках, чертежах и в тексте должны совпадать.

5. Для замечаний рецензента на каждой странице тетради оставлять поля шириной 4 см.

6. В конце работы представить список использованной литературы.

7. Контрольная работа выполняется и подписывается лично студентом. В противном случае она не будет зачтена даже при условии верного решения всех задач.

8. Контрольную работу сдать на проверку за 10 дней до начала очередной сессии.

9. После получения зачтенной работы студент обязан устранить в ней отмеченные рецензентом недостатки. В случае незачета студент должен в кратчайший срок устранить недостатки, указанные рецензентом, и представить работу на повторное рецензирование, приложив и ее первоначальный вариант.

10. На экзамене студент обязан представить прорецензированную и зачтенную работу. При необходимости (по требованию преподавателя) студент должен дать устные пояснения по любой из задач контрольной работы.

Работы, выполненные без соблюдения вышеназванных правил, не засчитываются и возвращаются студенту для переработки

КОНТРОЛЬНАЯ РАБОТА № 1

ЗАДАЧА 1. Завод выпускает 3 вида товаров Р₁, Р₂, Р₃. Производство единицы товара Р_i требует потребления определенного количества а_ij, i = 1, 2, 3, j = 1, 2, 3, каждого из имеющихся трех видов ресурсов R₁, R₂, R₃. Требуется определить, какое количество x₁, x₂, x₃ каждого товара может выпускать завод, потребив полностью заданное количество r₁, r₂, r₃ ресурсов вида R₁, R₂, R₃ соответственно. Составить систему линейных алгебраических уравнений, исследовать ее на совместность и решить тремя способами: а) матричным, б) с помощью формул Крамера, в) методом Гаусса. Значения а_ij и r_i (i = 1, 2, 3, j = 1, 2, 3) приведены в таблице 1.

Таблица 1

№	а11	а12	а13	а21	а22	а23	а31	а32	а33	r1	r2	r3
1	21	31	41	15	26	25	21	15	17	2060	1420	1020
2	12	14	17	11	13	9	22	7	10	910	640	660
3	11	13	15	22	17	13	33	25	20	820	950	1430
4	13	20	17	26	15	20	26	20	17	1040	1160	1170
5	25	20	19	50	30	27	75	27	40	1220	1910	2490
6	17	27	30	17	30	30	34	30	25	1610	1670	1690
7	18	22	17	54	20	25	36	30	25	1130	1690	1710
8	22	20	27	44	30	45	33	20	40	1430	2390	1930
9	30	23	40	60	50	47	60	45	37	1960	3010	2610
10	40	30	37	40	25	31	80	30	37	2110	1830	2510
11	21	31	41	15	26	25	21	15	17	2153	1486	1073
12	12	14	17	11	13	9	22	7	10	953	673	699
13	11	13	15	22	17	13	33	25	20	854	1002	1508
14	13	20	17	26	15	20	26	20	17	1090	1221	1233
15	25	20	19	50	30	27	75	27	40	1284	2017	2632
16	17	27	30	17	30	30	34	30	25	1684	1747	1779
17	18	22	17	54	20	25	36	30	25	1187	1789	1801
18	22	20	27	44	30	45	33	20	40	1499	2509	2023
19	30	23	40	60	50	47	60	45	37	2053	3167	2752
20	40	30	37	40	25	31	80	30	37	2217	1926	2657
21	21	31	41	15	26	25	21	15	17	2246	1552	1126
22	12	14	17	11	13	9	22	7	10	996	706	738
23	11	13	15	22	17	13	33	25	20	893	1054	1586
24	13	20	17	26	15	20	26	20	17	1140	1282	1296
25	25	20	19	50	30	27	75	27	40	1348	2124	2774
26	17	27	30	17	30	30	34	30	25	1758	1824	1868
27	18	22	17	54	20	25	36	30	25	1244	1888	1892
28	22	20	27	44	30	45	33	20	40	1568	2628	2116
29	30	23	40	60	50	47	60	45	37	2146	3324	2894
30	40	30	37	40	25	31	80	30	37	2324	2022	2804
31	21	31	41	15	26	25	21	15	17	2339	1618	1179
32	12	14	17	11	13	9	22	7	10	1039	739	777
33	11	13	15	22	17	13	33	25	20	932	1106	1664
34	13	20	17	26	15	20	26	20	17	1190	1343	1359
35	25	20	19	50	30	27	75	27	40	1412	2231	2916
36	17	27	30	17	30	30	34	30	25	1832	1901	1957
37	18	22	17	54	20	25	36	30	25	1301	1987	1983
38	22	20	27	44	30	45	33	20	40	1637	2747	2209
39	30	23	40	60	50	47	60	45	37	2239	3481	3036
40	40	30	37	40	25	31	80	30	37	2431	2118	2951

ЗАДАЧА 2. Найти каноническое уравнение линии, для каждой точки которой отношение расстояния до точки F(F_x, F_y) (фокус) к расстоянию до прямой х = А (директриса) есть величина постоянная, равная Е (эксцентриситет). Определить вид линии, сделать чертеж.

Все необходимые числовые данные по каждому варианту приведены в таблице 2.

Таблица 2

Номер варианта	Координаты фокуса F(Fx, Fy)	Директриса х = А	Эксцентриситет Е
1	(-2, 0)	-22/3	3/5
2	(4, 0)	28/3	3/5
3	(-1, 1)	-19/3	3/5
4	(0, 1)	-16/3	3/5
5	(-3, 0)	-21/4	4/5
6	(5, 0)	29/4	4/5
7	(-2, 1)	-17/4	4/5
8	(-1, 1)	-13/4	4/5
9	(-4, 0)	-164/5	5/13
10	(0, 0)	-144/5	5/13
11	(0, 1)	144/5	5/13
12	(-5, 1)	119/5	5/13
13	(0, 5)	-64/6	3/5
14	(1, 4)	-58/6	3/5
15	(-1, 3)	58/6	3/5
16	(6, 1)	21/5	5/4
17	(4, 2)	11/5	5/4
18	(0, 3)	9/5	5/4
19	(0, 3)	-9/5	5/4
20	(1, 2)	14/5	5/4
21	(-1, 2)	-14/5	5/4
22	(9, 3)	36/5	5/4
23	(-1, 2)	4/5	5/4
24	(-9, 3)	-36/5	5/4
25	(6, 1)	14/5	5/3
26	(4, 2)	4/5	5/3
27	(0, 3)	16/5	5/3
28	(0, 3)	-16/5	5/3
29	(1, 2)	21/5	5/3
30	(-1, 2)	-21/5	5/3
31	(7, 5)	3	1
32	(7, 1)	1	1
33	(6, 3)	2	1
34	(2, -2)	-6	1
35	(3, 5)	7	1
36	(1, 1)	7	1
37	(-1, 2)	7	1
38	(1, 3)	-1	1
39	(2, 5)	0	1
40	(-4, 0)	-2	1

ЗАДАЧА 3. Даны точки А (х₁; у₁; z₁), В (х₂; у₂; z₂), С (х₃; у₃; z₃), D (х₄; у₄; z₄), являющиеся вершинами треугольной пирамиды. Требуется:

1) записать уравнение плоскости ABC и представить его в общем виде и в отрезках, а также построить плоскость ABC, используя ее уравнение в отрезках;

2) вычислить угол между ребрами АВ и АС;

3) записать канонические уравнения прямой АВ;

4) найти площадь грани ABC;

5) вычислить объем пирамиды;

6) найти расстояние от точки D до ребра АВ и до грани ABC пирамиды.

Расчеты производить, округляя результаты до двух знаков после запятой.

Необходимые для расчетов данные приведены в таблице 3.

Таблица 3

Учебный номер	х1	у1	z1	х2	у2	z2	х3	у3	z3	х4	у4	z4
1	2	4	1	3	6	2	4	-1	-3	0	-2	5
2	1	-3	2	1	-1	1	2	1	-3	2	4	6
3	4	1	-3	3	4	2	2	4	1	1	-3	4
4	1	-3	1	0	1	3	0	-1	3	2	3	-5
5	-2	0	2	1	-2	1	2	-1	-2	1	4	3
6	2	1	1	1	-4	-1	-1	8	3	0	-4	6
7	2	4	1	3	4	2	4	1	-3	0	-3	5
8	4	-2	4	10	2	12	1	2	2	1	-3	-5
9	1	-1	1	2	3	1	4	5	1	-2	1	6
10	1	1	2	2	1	1	1	-2	3	0	-1	5
11	1	-1	2	1	3	-4	-5	3	-3	1	2	4
12	0	-1	1	1	2	-5	4	3	-2	-1	3	5
13	2	-1	0	3	2	1	1	3	4	2	-2	6
14	2	-1	1	1	3	-2	3	2	-5	2	4	6
15	2	3	5	-4	3	1	2	1	2	0	4	-6
16	1	0	-5	-2	3	2	1	-2	0	1	-1	6
17	3	-6	-1	1	-1	3	1	2	5	2	3	-5
18	5	-1	7	2	1	1	1	-3	0	-4	-1	3
19	3	2	2	1	-5	-8	4	2	1	1	-4	3
20	3	-3	4	1	-1	2	3	0	-5	0	-1	3
21	1	-3	4	1	-1	2	1	0	5	-4	0	2
22	3	7	-4	-2	0	4	-4	1	3	6	5	2
23	0	1	2	0	4	3	-4	2	-2	4	-3	-5
24	3	1	2	4	-1	0	0	7	0	3	-3	4
25	2	2	2	-2	-2	2	3	-2	0	0	0	7
26	2	2	-5	4	-4	0	0	0	2	4	2	6
27	0	4	-3	0	1	1	5	0	2	3	-3	4
28	1	1	2	-2	2	0	-2	-2	0	3	-3	-4
29	1	1	2	0	1	0	3	-4	0	2	-2	5
30	3	-2	-4	7	0	1	-4	4	3	0	6	7
31	1	-1	7	3	4	0	2	0	0	4	-3	-5
32	0	0	4	3	-2	0	-2	-2	2	4	6	3
33	4	2	2	-4	2	0	0	-5	2	0	5	6
34	5	0	0	0	4	1	2	-3	1	3	2	5
35	0	2	1	2	-2	1	0	-2	4	3	3	5
36	-2	2	1	2	-2	1	0	0	2	1	-1	5
37	1	1	1	4	-4	3	-2	2	0	3	2	-5
38	1	3	0	1	-4	1	2	0	0	0	1	6
39	2	-2	-2	1	1	4	0	2	0	1	-4	6
40	0	-4	0	4	2	1	3	-2	2	2	1	6

ЗАДАЧА 4. Фирма по производству одежды шьет мужские и женские пальто. На пошив одного мужского пальто требуется m₁ чел./дней, женского – m₂ чел./дней. Стоимость ткани для изготовления мужского пальто равна р₁ у.е., женского – р₂ у.е. Прибыль от одного мужского пальто составляет 3 у.е., женского – 2 у.е. Пошив пальто ограничен следующими обстоятельствами:

а) по контракту фирма должна сшить, по меньшей мере, n₁ мужских пальто и n₂ – женских;

б) на пошив пальто может быть затрачено не более К чел./дней;

в) затраты на материалы не должны превышать М у.е.;

г) прибыль должна быть не меньше Р у.е.

Используя данные таблицы 4, составить систему неравенств, удовлетворяющую ограничениям задачи.

Изобразить графически область допустимых значений количества производимых мужских и женских пальто, соответствующую ограничениям задачи, и указать одно из возможных значений этой области.

Таблица 4

№ варианта	m1	m2	р1	р2	n1	n2	К	М	Р
1	10	5	5	8	24	18	500	400	50
2	12	8	6	9	21	14	400	300	45
3	8	12	9	6	22	16	300	200	30
4	9	6	4	6	20	18	300	250	35
5	8	10	6	5	15	12	520	620	80
6	10	8	5	6	12	15	540	640	70
7	12	14	8	6	4	7	510	610	75
8	11	13	9	12	11	14	500	600	60
9	7	11	8	10	9	12	450	550	55
10	6	10	7	11	8	10	400	500	50
11	9	12	6	12	9	11	420	520	40
12	14	12	8	6	8	10	400	500	45
13	8	10	5	6	12	15	520	600	75
14	12	8	7	10	15	10	530	630	70
15	9	10	6	11	14	12	510	610	60
16	14	10	9	10	15	12	550	650	80
17	7	9	4	3	12	16	300	550	40
18	8	6	10	5	12	15	500	600	60
19	12	10	8	7	14	16	540	620	75
20	11	14	9	12	6	9	400	500	60
21	12	9	14	6	12	10	420	520	70
22	7	11	10	9	14	12	400	480	55
23	5	4	4	10	12	10	350	450	50
24	6	5	6	12	8	11	320	420	45
25	8	12	10	11	9	13	450	600	60
26	7	11	12	10	13	9	460	610	75
27	9	12	10	12	14	8	520	620	80
28	10	14	9	11	15	10	540	640	80
29	11	12	10	12	14	12	510	610	70
30	12	14	9	12	10	10	500	600	80
31	5	10	8	5	18	24	400	500	50
32	6	9	6	9	20	22	410	480	60
33	7	10	4	10	22	24	420	460	70
34	8	11	5	10	16	18	430	440	80
35	9	12	8	9	15	20	440	420	90
36	10	14	9	12	20	15	450	400	80
37	11	15	10	15	12	16	460	640	70
38	12	16	12	15	16	12	470	600	60
39	14	8	8	10	20	15	480	520	50
40	7	14	10	15	15	20	500	400	40

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

ЗАДАЧА 1 (вариант…). Завод выпускает 3 вида товаров Р₁, Р₂, Р₃. Производство единицы товара Р_i требует потребления определенного количества a_ij, i = 1, 2, 3, j = 1, 2, 3 каждого из имеющихся трех видов ресурсов R₁, R₂, R₃. Требуется определить, какое количество x₁, x₂, x₃ каждого товара может выпускать завод, потребив полностью заданное количество r₁, r₂, r₃ ресурсов вида R₁, R₂, R₃ соответственно. Составить систему линейных алгебраических уравнений, исследовать ее на совместность и решить тремя способами: а) матричным, б) с помощью формул Крамера, в) методом Гаусса.

Решение. Пусть а₁₁ = 21, а₁₂ =31, а₁₃ = 41, а₂₁ = 15, а₂₂ = 26, а₂₃ = 25, а₃₁ = 21, а₃₂ = 15, а₃₃ =17, r₁ = 2432, r₂ = 1684, r₃ = 1232.

Система линейных алгебраических уравнений при данных значениях a_ij, r_i имеет вид:

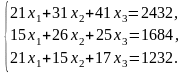
Исследуем построенную систему на совместность. Для этого используем теорему Кронекера-Капелли. Основная матрица системы и расширенная матрица системы имеют вид:

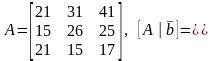
Найдем ранги основной и расширенной матриц системы:

Таким образом, с помощью элементарных преобразований мы привели расширенную матрицу системы к трапециевидной. Так как число ненулевых диагональных элементов главного минора равно 3, то ранг расширенной и основной матриц (в данном случае) равен 3.

Тогда по теореме Кронекера-Капелли исходная система уравнений совместна, причем, так как 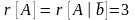и n = 3, то система имеет единственное решение. Найдем его тремя способами.

а) Матричный способ.

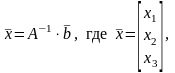
А^-1 – обратная матрица к А, 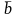– столбец свободных членов.

Строим А^-1.

1) Вычислим определитель матрицы А:

2) Строим матрицу из алгебраических дополнений к элементам матрицы А:

3) Транспонируем полученную матрицу А¢, в результате получим присоединенную матрицу :

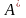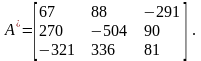
4) Тогда, обратная матрица А^-1 будет иметь вид:

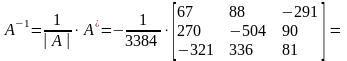
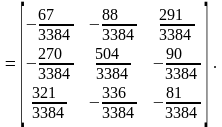
5) Проверим правильность построения обратной матрицы:

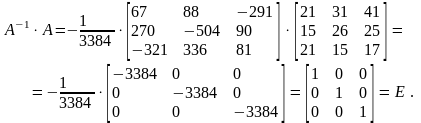
В итоге, обратная матрица построена верно. (Вообще говоря, необходимо также проверить А · А^-1 = Е. Проверьте самостоятельно.)

Находим решение исходной системы:

Таким образом, исходная система имеет решение: х₁ = 14, х₂ = 24, х₃ = 34.

б) Нахождение решения системы с помощью формул Крамера.

Формулы Крамера для нашей системы будут иметь вид:

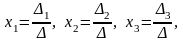
где D = 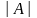= –3384. Здесь D₁, D₂, D₃ – определители матриц А₁, А₂, А₃, которые получаются из матрицы А заменой первого, второго и третьего столбцов на столбец свободных членов соответственно. Так как D ¹ 0, то решение системы единственное. Найдем определители системы D₁, D₂, D₃:

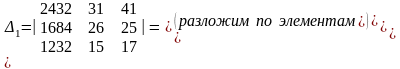
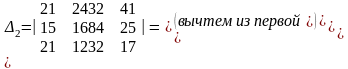
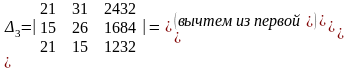
Следовательно,

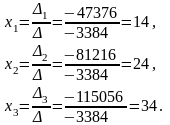
в) Решение системы методом Гаусса.

Так как расширенная матрица системы приведена выше к виду 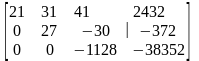, то исходная система уравнений равносильна системе:

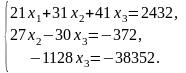
Из последнего уравнения имеем, что

Подставим х₃ в предпоследнее уравнение:

27х₂ – 30 · 34 = –372,

27х₂ – 1020 = –372,

27х₂ = 648,

х₂ = 24.

Подставим х₂ и х₃ в первое уравнение:

21х₁ – 31 · 24 + 41 · 34 = 2432,

21х₁ + 2138 = 2432,

21х₁ = 294,

х₁ = 14.

Таким образом, мы нашли решение исходной системы методом Гаусса:

х₁ = 14, х₂ = 24, х₃ = 34.

Ответ: завод может выпустить 14 единиц товара первого вида, 24 единицы товара второго вида и 34 единицы товара третьего вида, потребив полностью заданное количество ресурсов.

ЗАДАЧА 2 (вариант …). Найти каноническое уравнение линии, для каждой точки которой отношение расстояния от точки F(–7, 2) (фокус) к расстоянию до прямой х = –26/5 (директриса) есть величина постоянная, равная Е = 5/4 (эксцентриситет). Определить вид линии, сделать чертеж.

Решение. Сделаем условный чертеж (см. рис. 1). В выбранной системе координат построим директрису, заданную уравнением х = –26/5, и фокус F(–7, 2).

Так как по условию эксцентриситет Е = 5/4 > 1, то искомой линией будет являться гипербола, и поскольку директриса х = –26/5 параллельна оси Oy, то ее каноническое уравнение будет иметь вид:

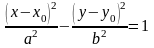. (1)

Здесь точка М₀(х₀, у₀) – центр гиперболы,

а – действительная полуось,

b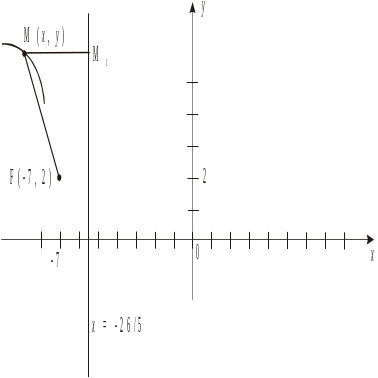 – мнимая полуось.

Рис. 1

Примечания:

Если Е < 1, то искомой линией будет являться эллипс с каноническим уравнением .

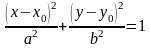Если Е = 1, то искомой линией будет являться парабола с каноническим уравнением

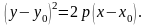
Пусть М(х, у) – произвольная точка гиперболы, MF – расстояние от точки М до фокуса F, ММ₁ – расстояние от точки М до директрисы. Тогда по условию задачи

. (2)

Вычислим MF и MM₁.

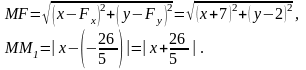
Подставив найденные выражения в уравнение (2), получим:

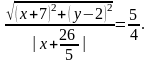
Преобразуем полученное уравнение к виду (1). Для этого возведем обе части уравнения в квадрат, избавимся от знаменателя, и приведем подобные члены. Получим:

Выделим полный квадрат в первой скобке по переменной х, и произведем равносильные преобразования:

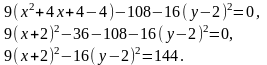
Разделив обе части уравнения на 144, получим:

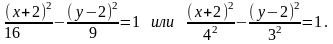
Получив каноническое уравнение гиперболы с центром в точке М₀(–2, 2), а = 4 – действительная полуось, b = 3 – мнимая полуось, сделаем чертеж:

Рис. 2

На рис. 2 O¢ x¢ y¢ – новая система координат с началом О¢ в точке М₀(–2, 2).

Ответ: 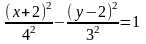– гипербола.

ЗАДАЧА 3 (вариант…). Даны точки А (х₁; у₁; z₁), В (х₂; у₂; z₂), С (х₃; у₃; z₃), D (х₄; у₄; z₄), являющиеся вершинами треугольной пирамиды. Требуется:

1) записать уравнение плоскости АВС и представить его в общем виде и в отрезках, а также построить плоскость АВС, используя ее уравнение в отрезках;

2) вычислить угол между ребрами АВ и АС;

3) записать канонические уравнения прямой АВ;

4) найти площадь грани АВС;

5) вычислить объем пирамиды;

6) найти расстояние от точки D до ребра АВ и до грани АВС пирамиды.

Р ешение. Пусть х₁ =3, у₁ = 1, z₁ = 2, х₂ = –2, у₂ = 0, z₂ = –4, х₃ = 0, у₃ = 8, z₃ = 2, х₄ = 4, у₄ = 4, z₄ = 0.

Тогда имеем вершины пирамиды:

А(3; 1; 2), В(–2; 0; –4), С(0; 8; 2), D(4; 4; 0).

О

Рис. 3

братим внимание, что строить пирамиду не обязательно, но для лучшего понимания задачи пусть пирамида АВСD имеет вид, приведенный на рис. 3.

1) По координатам точек А, В, С находим уравнение плоскости, проходящей через три заданные точки А, В, С:

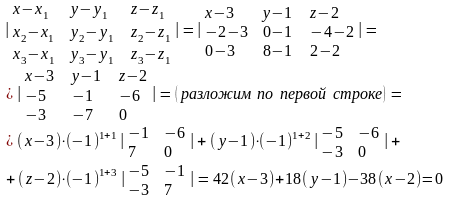
Сократим на 2 полученное уравнение:

21(х – 3) + 9(у – 1) – 19(z – 2) = 0. (3)

(3) – уравнение плоскости АВС, заданной точкой А(3; 1; 2) и нормальным вектором 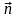= (21; 9; –19).

Раскрыв скобки в уравнении (3), получим требуемое общее уравнение плоскости АВС:

21х – 63 + 9у – 9 – 19z + 38 = 0, Þ 21х + 9у – 19z – 34 = 0 . (4)

Приведем данное уравнение плоскости (4) к виду уравнения плоскости в отрезках:

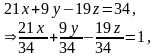
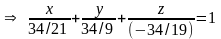. (5)

(5) – уравнение плоскости АВС в отрезках, причем

Построим плоскость АВС, используя уравнение в отрезках (5):

Рис. 4

2) Угол между ребрами АВ и АС равен углу между векторам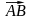и и 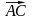. Из скалярного произведения векторов и имеем:

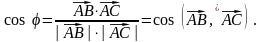
Найдем координаты векторов и :

= (–2 – 3; 0 – 1; –4 – 2) = (–5; –1; –6),

= (0 – 3; 8 – 1; 2 – 2) = (–3; 7; 0).

Следовательно,

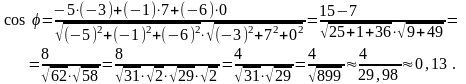
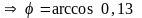» 1,44 рад » 82°30¢.

3) Запишем канонические уравнения прямой АВ:

где (х₀; у₀; z₀) – координаты точки М, через которую проходит прямая АВ;

(m; n; p) – координаты направляющего вектора 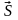прямой АВ. В данном случае в качестве точки М возьмем точку А(3; 1; 2) Î АВ. Следовательно, канонические уравнения прямой АВ имеют вид:

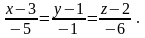
4) Найти площадь грани АВС. Грань АВС – треугольник. Из геометрического смысла векторного произведения двух векторов следует, что длина вектора [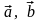 ] численно равна площади параллелограмма, построенного на этих векторах. Следовательно, площадь ΔАВС будет вычисляться по формуле:

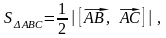
Значит,

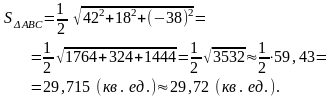
5) Вычислим объем пирамиды АВСD. Объем пирамиды равен объема параллелепипеда, построенного на векторах 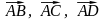. В свою очередь, объем параллелепипеда равен модулю смешанного произведения этих векторов. Найдем смешанное произведение векторов . Координаты векторов и найдены в п. 2. Найдем координаты вектора :

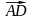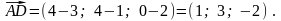
Следовательно,

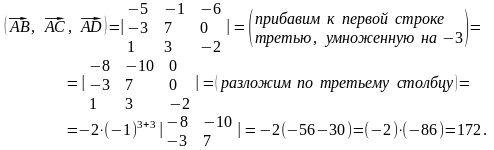
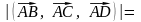
Так как смешанное произведение больше нуля, то 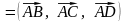Þ V_пар = 172 (куб. ед.).

Таким образом,

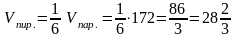(куб. ед.).

6) Найти расстояние от точки D до ребра АВ и до грани АВС пирамиды.

Расстояние от точки D до ребра АВ – это расстояние от точки D до прямой АВ. Воспользуемся формулой 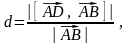которая получается из формулы площади DADB с учетом формулы 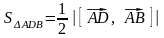и формулы

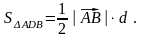
В нашем случае вектор 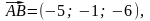вектор (см. выше). Находим длину вектора :

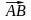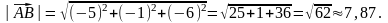
Находим далее векторное произведение :

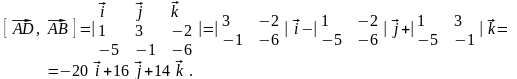
Следовательно,

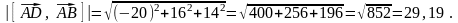
Тогда

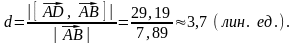
Расстояние от точки D до грани АВС пирамиды – это расстояние от точки D до плоскости АВС. Для нахождения этого расстояния воспользуемся формулой:

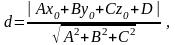
где Ах + Ву + Сz + D = 0 – общее уравнение плоскости АВС, (х₀; у₀; z₀) – координаты точки D.

В нашем случае общее уравнение плоскости АВС будет:

21х + 9у – 19z – 34 = 0, где точка D(4; 4; 0).

Тогда

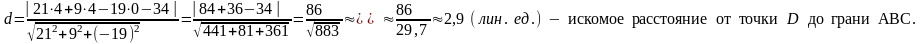
Ответы: 1) 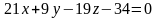 – уравнение плоскости АВС, – уравнение плоскости АВС в отрезках;

2) 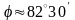– угол между ребрами АВ и АС;

3) 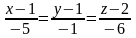– канонические уравнения прямой АВ;

4) 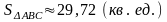– площадь грани АВС;

5) 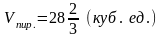– объем пирамиды АВСD;

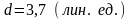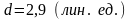6)  – расстояние от точки D до ребра АВ; – расстояние от точки D до грани АВС.

ЗАДАЧА 4 (вариант…). Фирма по производству одежды шьет мужские и женские пальто. На пошив одного мужского пальто требуется 2 чел./дня, женского – 3 чел./дня. Стоимость ткани для изготовления мужского пальто равна 4 у.е., женского – 5 у.е. Прибыль от одного мужского пальто составляет 3 у.е., женского – 2 у.е. Пошив пальто ограничен следующими обстоятельствами:

а) по контракту фирма должна сшить, по меньшей мере, 6 мужских пальто и 4 – женских;

б) на пошив пальто может быть затрачено не более 120 чел./дней;

в) затраты на материалы не должны превышать 140 у.е.;

г) прибыль должна быть не меньше 30 у.е.

Составить систему неравенств, удовлетворяющую ограничениям задачи. Изобразить графически область допустимых значений количества производимых мужских и женских пальто, соответствующую ограничениям задачи, и указать одно из возможных значений этой области.

Решение. Пусть х – количество производимых мужских пальто, y – женских. Заметим, что х и у, по смыслу задачи, должны принимать только целые положительные значения. Составим систему неравенств, удовлетворяющую ограничениям задачи:

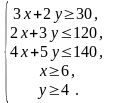(6)

На рис. 5 изображена область допустимых значений количества производимых мужских и женских пальто, соответствующая ограничениям задачи. Эта область выделена штриховкой.

Заменим систему неравенств системой соответствующих равенств:

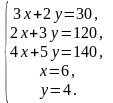(7)

Каждое из уравнений системы равенств описывает множество точек плоскости Оху, принадлежащих прямой линии. В свою очередь каждая из прямых линий разбивает плоскость Оху на две части (полуплоскости). Решением соответствующего неравенства из системы (6) будет лишь одна из этих полуплоскостей. Для того, чтобы определить, какая из полуплоскостей будет решением, необходимо взять координаты любой точки плоскости Оху и подставить в соответствующее неравенство. Если в итоге получается верное неравенство, то полуплоскость, которой принадлежит данная точка, будет решением данного неравенства, если нет, – то противо- положная полуплоскость. Как правило, для подстановки используется точка О(0; 0) – начало координат, если соответствующая прямая не проходит через О(0; 0), или любая другая точка, не лежащая на данной прямой линии.

Подставим координаты точки О(0; 0) в первые три неравенства системы (6).

1

) 3 · 0 + 2 · 0 ³ 30 Þ 0 ³ 30 – неверно. Следовательно, решением данного неравенства является полуплоскость, которой не принадлежит начало координат. Так как неравенство не строгое, то сама граница (прямая линия) входит в множество решений неравенства.

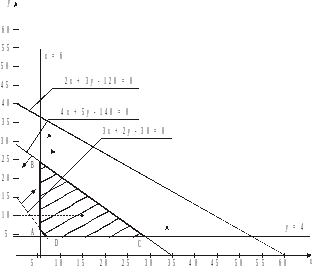
Рис. 5

2) 2 · 0 + 3 · 0 £ 120 Þ 0 £ 120 – верно. Следовательно, решением данного неравенства является полуплоскость, которой принадлежит начало координат, включая границу.

3) 4 · 0 + 4 · 0 £ 140 Þ 0 £ 140 – верно. Следовательно, решением данного неравенства также является полуплоскость, которой принадлежит начало координат, включая границу.

4) Очевидно, что неравенство х ³ 6 определяет полуплоскость, включая границу (х = 6), которая находится правее прямой х = 6, а неравенство у ³ 4 определяет полуплоскость, включая границу (у = 4), которая находится выше прямой у = 4.

Таким образом, мы решили каждое из неравенств системы (6). Осталось определить ту область, если она есть, плоскости Оху, в которой все пять неравенств одновременно имеют решение. Построим на плоскости Оху все пять линий системы (7), отметим стрелками направления решений каждого из неравенств системы (6), в результате получим область, которая является общей для всех пяти неравенств системы (6) (см. рис. 5). В нашем случае эта область представляет собой четырехугольник, который для наглядности выделен штриховкой.

Одно из возможных допустимых значений области – x = 15, y = 10.

Ответ: область допустимых значений количества производимых мужских и женских пальто представляет собой четырехугольник АВСD вместе с границами.

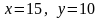– одно из возможных допустимых значений области.