Контрольная №1. Вариант 30

Задание 1. Зашифровать данный текст, используя таблицу ASCII-кодов: Printer.

Решение:

P - 80; r - 114; i - 105; n - 110; t - 116; e - 101; r - 114

Ответ: 80 114 105 110 116 101 114.

Задание 2. Дешифровать данный текст, используя таблицу ASCII-кодов:

Решение:

43 4F 4D 50 55 54 45 52

43 - C; 4F - O; 4D - M; 50 - P; 55 - U; 54 - T; 45 - E; 52 - R

Ответ: COMPUTER.

Задание 3. Записать прямой код числа, интерпретируя его как восьмибитовое целое без знака: а) 235₁₀; б) 239₁₀; в) 160₁₀.

Решение:

а) 235₁₀ = 11101011₂; прямой код: 011101011;

б) 239₁₀ = 11101111₂; прямой код: 011101111;

в) 160₁₀ = 10100000₂; прямой код: 010100000;

Ответ: Прямой код числа, интерпретируя его как восьмибитовое целое без знака a) 011101011; б) 011101111; в) 010100000;

Задание 4. Записать дополнительный код числа, интерпретируя его как восьмибитовое целое со знаком:

а) 20₁₀; б) -28₁₀; в) -123₁₀.

Решение:

Дополнительный код числа - это обратный код, к младшему значащему разряду которого прибавлена единица.

а) 20₁₀;

представление положительного числа: 00010100;

обратный код: 00010100;

дополнительный код: 00010100.

б) -28₁₀;

представление положительного числа: 00011100;

обратный код: 11100011;

дополнительный код: 11100011 + 1 = 11100100.

в)-123₁₀;

представление положительного числа: 01111011;

обратный код: 10000100;

дополнительный код: 10000100 + 1 = 10000101;

Ответ: а) дополнительный код: 00010100; б) дополнительный код: 11100100; в) дополнительный код: 10000101;

Задание 3а. Записать прямой код числа, интерпретируя его как шестнадцатибитовое целое без знака:

а) 29777₁₀; б) 30982₁₀.

Решение:

а) 29777₁₀ = 111010001010001₂; прямой код: 0111010001010001;

б) 30982₁₀ = 111100100000110₂; прямой код: 0111100100000110;

Ответ: а) прямой код: 0111010001010001; б) прямой код: 0111100100000110;

Задание 4а. Записать дополнительный код числа, интерпретируя его как шестнадцатибитовое целое со знаком:

а) 18276₁₀; б) -19193₁₀.

Решение:

а) 18276₁₀;

представление положительного числа: 0100011101100100;

обратный код: 0100011101100100;

дополнительный код: 0100011101100100.

б) -19193₁₀

представление положительного числа: 0100101011111001;

обратный код: 1011010100000110;

дополнительный код: 1011010100000110 + 1 = 1011010100000111.

Ответ: а) дополнительный код: 0100011101100100; б) дополнительный код: 1011010100000111.

Задание 5. Записать в десятичной системе счисления целое число, если дан его дополнительный код:

а) 0001111011110110; б) 1000111010110111

Решение:

а) 0001111011110110

В старшем разряде ноль, значит, закодировано положительное число. Просто переведем число в десятичную систему счисления.

0001111011110110₂ = 7926₁₀;

б) 1000111010110111;

В старшем разряде единица, значит, закодировано отрицательное число. Воспользуемся соответствующим алгоритмом: из двоичного представления вычесть единицу, инвертировать биты, перевести в десятичную систему счисления.

1) 1000111010110111₂ - 1₂ = 1000111010110110₂;

2) инвертируем биты: 0111000101001001;

3) 0111000101001001₂ = 29001₁₀;

Ответ: а) 7926₁₀; б) -29001₁₀;

Задание 6-1. Записать код действительного числа, интерпретируя его как величину типа Double, результат закодировать в шестнадцатеричной системе счисления:

а) -761,375; б) 290,15625.

Решение:

а) -761,375;

Воспользуемся алгоритмом для кодирования действительного числа:

1) Переводим модуль числа в двоичную систему:

| -761,375₁₀ | = 761,375₁₀ = 1011111001,011₂;

2) Нормализуем мантиссу:

1011111001,011₂ = 1,011111001011₂ * 2⁹;

Умножаем на 2 в степени 9, так как сдвинули запятую на 9 разрядов.

М = 011111001011 - мантисса.

Р = 9 - порядок

3) Прибавляем к порядку смещение. Для типа double смещение = 1023.

Рсмещѐнный = 9 + 1023 = 1032₁₀ = 10000001000₂;

4) Исходное число отрицательное, то представление знака = 1.

5) В мантиссу вписываем только еѐ дробную часть. Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.

0111 1100 1011 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

Запишем число:

1 10000001000 0111 1100 1011 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

В шестнадцатеричной системе счисления C087CB0000000000₁₆.

Ответ: код действительного числа -761,375, интерпретируя его как величину типа Double 1 10000001000 0111 1100 1011 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000. В шестнадцатеричной системе счисления C087CB0000000000₁₆.

б) 290,15625;

Воспользуемся алгоритмом для кодирования действительного числа:

1) 290,15625₁₀ = 100100010,00101₂;

2) Нормализуем мантиссу:

100100010,00101₂ = 1,0010001000101 * 2⁸;

Умножаем на 2 в степени 8, так как сдвинули запятую на 8 разрядов.

М = 0010001000101 - мантисса.

Р = 8 - порядок

3) Прибавляем к порядку смещение. Для типа double смещение = 1023.

Рсмещѐнный = 8 + 1023 = 1031₁₀ = 10000000111₂;

4) Исходное число положительное, то представление знака = 0.

5) В мантиссу вписываем только еѐ дробную часть. Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.

0010 0010 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000

Запишем число:

0 10000000111 0010 0010 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000

В шестнадцатеричной системе счисления: 4072228000000000₁₆.

Ответ: код действительного числа 290,15625, интерпретируя его как величину типа Double 0 10000000111 0010 0010 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000. В шестнадцатеричной системе счисления 4072228000000000₁₆.

Задание 6-2. Дан код величины типа Double, записанный шестнадцатеричными цифрами. Преобразовать его в число:

а) 4070C28000000000; б) 4055980000000000.

Решение:

а) 4070C28000000000.

Представим в двоичном коде:

0 10000000111 0000 1100 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000, где

S = 0 (положительное число)

P = 100000001112 = 1031 - 1023 = 8

M = 0000110000101

N = 1,0000110000101

С учетом P = 8, N = 100001100,00101

100001100₂ = 28*1 + 2⁷*0 + 2⁶*0 + 2⁵*0 + 2⁴*0 + 2³*1 + 2²*1 + 2¹*0 + 2⁰*0 = 268₁₀.

Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда.

00101₂ = 2^-1*0 + 2^-2*0 + 2^-3*1 + 2^-4*0 + 2^-5*1 = 0.15625

б) 4055980000000000.

Представим в двоичном коде:

0 10000000101 0101 1001 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000, где

S = 0 (положительное число)

P = 10000000101₂ = 1029 - 1023 = 6

M = 010110011

N = 1,010110011

С учетом P = 6, N = 1010110,011

1010110,011₂ = 86,375₁₀.

Ответ: а) 268,15625. б) 86,375.

Контрольные вопросы (краткие ответы)

1. Что такое кодирование информации в общем смысле?

В общем смысле кодирование информации можно определить как перевод информации, представленной сообщением в первичном алфавите, в последовательность кодов.

2. Что такое код? Приведите примеры кодирования и декодирования.

Код — система условных знаков для передачи, обработки и хранения информации. Кодирование — процесс представления информации в виде кода. Например, в памяти компьютера любая информация кодируется с помощью двоичного алфавита, содержащего всего два символа: 0 и 1. Декодирование - процесс обратного преобразования кода к форме исходной символьной системы, т.е. получение исходного сообщения. Например: перевод с азбуки Морзе в письменный текст на русском языке.

3. Приведите примеры искусственного повышения избыточности кода.

Многократная передача кодовых комбинаций (метод повторения), одновременная передачу кодовой комбинации по нескольким параллельно работающим каналам, помехоустойчивое (корректирующее) кодирование, т. е. использование кодов, исправляющих ошибки. Иногда применяют комбинации этих способов.

4. В чем состоит содержание 1-й и 2-й теорем Шеннона?

1 теорема - При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов.

2 теорема - Всякая машина Тьюринга  А может быть преобразована в эквивалентную машину С не более чем с двумя знаками внешнего алфавита.

5. Какие коды используются в вычислительной технике для кодирования букв русского алфавита?

В настоящее время существует 5 кодовых таблиц для русских букв: Windows (СР(кодовая страница)1251), MS – DOS (СР(кодовая страница)866), KOИ – 8 (Код обмена информацией, 8-битный) (используется в OS UNIX), Mac (Macintosh), ISO (OS UNIX).

6. Как кодируется графическая информация, если изображение черно-белое? цветное?

Если говорить о черно-белых иллюстрациях, то, если не использовать полутона, то пиксель будет принимать одно из двух состояний: светится (белый) и не светится (черный). А так как информация о цвете пикселя называется кодом пикселя, то для его кодирования достаточно одного бита памяти: 0 - черный, 1 - белый. Если говорить о кодировании цветных графических изображений, то нужно рассмотреть принцип декомпозиции произвольного цвета на основные составляющие. Применяют несколько систем кодирования: HSB, RGB и CMYK.

Контрольные вопросы (развернутые ответы)

1. Основные результаты теории кодирования

Теория кодирования - одна из центральных ветвей теории информации. Это прикладная математическая дисциплина, результаты которой используются, в частности, в теории связи, радиолокации, телемеханике и вычислительной технике.

Кодирование - одно из наиболее распространенных понятий в современной информатике. Что же такое "кодирование"? Под "кодированием" понимается операция отождествления символов или групп символов одного кода с символами или группами символов другого кода.

Необходимость кодирования возникает прежде всего из потребности приспособить форму сообщения к данному "каналу связи" или какому-либо устройству, предназначенному для преобразования или хранения информации.

Развитие современной теории кодирования стимулировалось прогрессом систем связи. Теория информации Шеннона, основанная на понятии энтропии, является математической основой эффективных кодов, широко используемых для сжатия информации. Их примерами являются коды Шеннона-Фано и код Хаффмена.

Потребность защитить информацию и системы связи от шумов способствовали развитию теории избыточных кодов. Код Хемминга, циклические коды - это хорошо известные примеры избыточных кодов.

Таким образом, современная теория кодирования - это совокупность, по крайней мере, четырех различных направлений:

1. Теория систем счисления;

2. Теория криптографии;

3. Теория эффективных кодов;

4. Теория избыточных кодов.

Для решения задач кодирования широко используется различный математический аппарат. Например, в теории алгебраических кодов широко используется аппарат теории групп, в современной криптографии основным математическим аппаратом является теория чисел.

2. Основные теоремы теории кодирования и их следствия.

Теорема 1. Неравенство Крафта.

В теории кодирования, неравенство Крафта — Макмиллана даёт необходимое и достаточное условие существования разделимых и префиксных кодов, обладающих заданным набором длин кодовых слов.

Теорема. Неравенство  является необходимым и достаточным условием существования кодовых слов, соответствующих концевым узлам дерева с длинами, равными kj.

Следствие. Можно обобщить неравенство Крафта для случаев, когда кодирующим алфавитом является k-ичный. В доказательстве изменятся некоторые пункты:

• отрезок 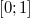 придется делить не 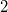на , а на 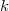 равных частей;

• соответственно неравенство примет вид: .

Теорема 2. Средняя длина кода   меньшая,  чем   является недостижимой ни при каком кодировании.

Доказательство:

Покажем, что

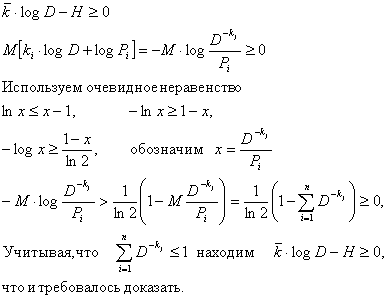
Теорема 3. Можно указать такой способ кодирования равно распределенных независимых сообщений, что средняя длина кода будет удовлетворять следующим требованиям:

Доказательство.

Пусть D=2, M=20. В этом диапазоне заведомо имеется одно целое число

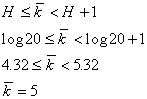
Теорема 4.  Существуют такие способы кодирования для достаточно длинного сообщения x1, x2, … , что средняя длина  кодового слова может быть сделана сколь угодно близкой к     .

Доказательство. Возьмем произвольное целое N>1 и разобьем последовательность x1, x2, … , на группы N случайных величин. Каждую такую группу будем рассматривать как одну случайную величину  Y=( x1, x2, … ,xN) и применим к ней теорему (3).

,

где HY=NHX ,    средняя длина слова, передающего сообщение  Y=( x1, x2, … ,xN). Очевидно, что  , тогда получим

Увеличивая N, Величину 1/N можно сделать сколь угодно малой, что доказывает теорему.

Список литературы

1. Аветисян Р.Д., Аветисян Д.В. Теоретические основы информатики. — М.: РГГУ, 1997.

2. Агеев В.М. Теория информации и кодирования: дискретизация и кодирование измерительной информации. — М.: МАИ, 1977.

3. Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс. — М.: Мир, 1976.

4. М.Брой. Информатика. В 3 томах. Т.2. Вычислительные структуры и машинно-ориентированное программирование. — М.: Диалог-МИФИ, 1996.

5. Дмитриев В.И. Прикладная теория информации. — М., 1989.

11