1.8.5. Частные производные

Рассмотрим функцию двух переменных U=f(x, y), заданную в виде таблицы U_ij=f(x, y), где x_i=x₀+ih_x (i=0,1,...,i), y_i=y₀+ih_y (j=0, 1,...,j). Используя понятие частной производной, можно приближенно записать для малых значений шагов h_y, h_y

Введем обозначения по правилам понятным из таблицы

y x	xi-2	xi-1	xi	xi+1	xi+2
yj-2	Ui-2,j-2	Ui-1,j-2	Ui,j-2	Ui+1,j-2	Ui+2,j-2
yj-1		Ui-1,j-1	Ui,j-1	Ui+1,j-1	Ui+2,j-1
yj		Ui-1,j	Ui,j	Ui+1,j	Ui+2,j
yj+1		Ui-1,j+1	Ui,j+1	Ui+1,j+1	Ui+2,j+1
yj+2				Ui+1,j+2	Ui+2,j+2

Тогда получим следующие приближенные выражения (аппроксимации) для частных производных в узлах х_i, y_j с помощью отношений конечных разностей:

.

Для численного дифференцирования функций многих переменных воспользуемся разложением в ряд Тейлора функции многих переменных

используем эту формулу дважды:

найдем U_i+1,j=f(x_i+h_x, y_j) при x=h_x, y=0;

найдем U_i-1,j=f(x_i-h_x, y_j) при x=-h_x, y=0;

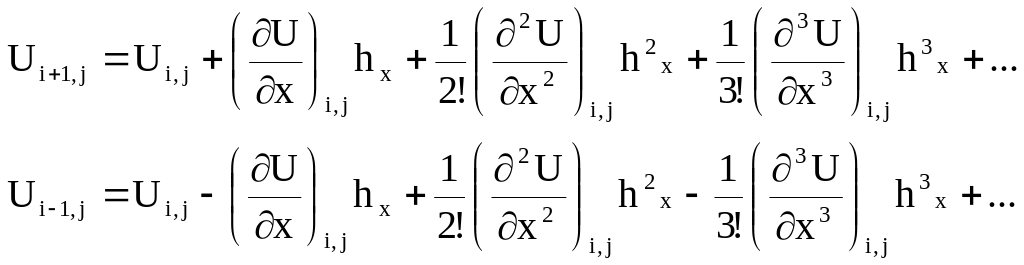
Вычтем из первого равенства второе:

Отсюда найдем аппроксимацию производной с помощью центральных разностей

Она имеет второй порядок.

Аналогично могут быть получены аппроксимации производной , а также старших производных. В частности для второй производной можно получить

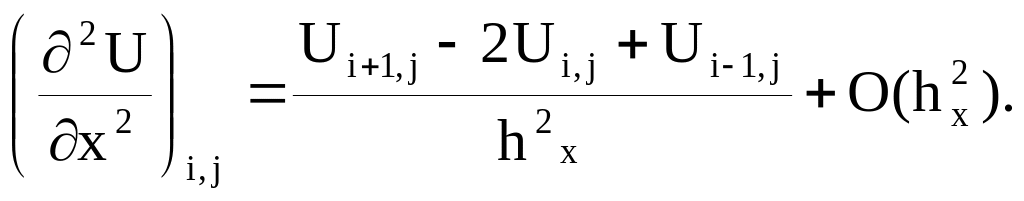
Записывая разложения в ряд при разных значениях x и y, можно вывести различные формулы численного дифференцирования с необходимым порядком аппроксимации.

Данные аппроксимации производных могут быть использованы при построении разностных схем для решения уравнений с частными производными.