
- •Числовой ряд. Сумма числового ряда.
- •Необходимое условие сходимости числового ряда. Гармонический ряд.
- •Комплексная форма ряда Фурье.
- •Основные элементарные функции комплексной переменной.
- •26. Предел и непрерывность функции комплексной переменной.
- •35.Особые точки аналитических функций.
- •51. Применение формулы Дюамеля при решении задачи Коши.
35.Особые точки аналитических функций.
Точка
называется нулем функции
,
если
 . В этом случае разложение функции
в окрестности точки
в степенной ряд не содержит нулевого
члена, т.к.
. В этом случае разложение функции
в окрестности точки
в степенной ряд не содержит нулевого
члена, т.к.
 .
Если не только
.
Если не только
 ,
но
,
но
 ,
а
,
а
 ,
то разложение функции
в окрестности точки
имеет вид
,
то разложение функции
в окрестности точки
имеет вид
 ,
а точка
называется нулем кратности m
(или нулем m-го
порядка). Если m=1,
то
называется простым нулем.
,
а точка
называется нулем кратности m
(или нулем m-го
порядка). Если m=1,
то
называется простым нулем.
Особой точкой функции называется точка, в которой функция не является аналитической.
Особая точка функции называется изолированной, если в некоторой окрестности ее функция не имеет других особых точек.
Если
-
изолированная особая точка функции
,
то существует такое число
, что в кольце
 .
Функция
будет аналитической и, следовательно,
разлагается в ряд Лорана:
.
Функция
будет аналитической и, следовательно,
разлагается в ряд Лорана:

При этом возможны следующие случаи:
Ряд Лорана не содержит главной части, т.е. в ряде нет членов с отрицательным показателем. В этом случае точка называется устранимой особой точкой функции .
Разложение Лорана содержит в своей части конечное число членов, т.е. в ряде есть коечное число членов с отрицательными показателями. В этом случае точка называется полюсом функции .
Разложение Лорана содержит в своей главной части бесконечное множество членов, т.е. в ряде есть бесконечно много членов с отрицательными показателями. В этом случае точка называется существенно особой точкой функции .
36. Вычеты и их вычисление.
Вычетом
аналитической функции
в изолированной особой точке
называется комплексное число, равное
значению интеграла
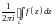 ,
взятого в положительном направлении
по окружности L
с центром в точке
,
лежащей в области аналитичности функции
(т.е. в кольце
).
,
взятого в положительном направлении
по окружности L
с центром в точке
,
лежащей в области аналитичности функции
(т.е. в кольце
).
Обозначается
вычет функции
в изолированной области особой точке
символом Res или Res
или Res .
Таким образом, Res
.
Таким образом, Res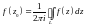
Если
в формуле
(
)
положить n
= -1, то получим
 или Res
или Res
 .
.
Полюс
Пусть точка
является простым полюсом функции
.Тогда
ряд Лорана для функции
в окрестности точки
имеет вид
 .Отсюда
.Отсюда
 .
.
Поэтому,
переходя в этом равенстве к пределу при
, получаем Res
Res
Пусть
точка
является полюсом m-го
порядка функции
.
Тогда лорановское разложение функции
в окрестности точки имеет вид
 . Отсюда
. Отсюда
 .
.
Дифференцируя
последнее равенство (m-1)
раз, получим:

Переходя
здесь к пределу при
,
получаем
Res
 .
.
37. Основная теорема Коши о вычетах.
Теорема(Коши)
Если функция
является аналитической в замкнутой
области
,
ограниченной контуром L,
за исключением конечного числа особых
точек
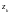 (
),
лежащих внутри области D,
то
(
),
лежащих внутри области D,
то
 .
.
38. Вычисление несобственных интегралов.
 -
несобственный интеграл.
-
несобственный интеграл.
Теорема
Пусть
аналитична в области
 (в верхней полуплоскости) за исключением
точки
(в верхней полуплоскости) за исключением
точки
 и непрерывна на оси OX.
и непрерывна на оси OX.
Пусть
несобственный интеграл
- сходится, а предел


При выполнении этих условий справедлива следующая формула
 .
.
Лемма
Жордана Пусть
функция
аналитична в области
всюду, за исключением конечного числа
особых точек, если
 на окружности достаточно большого
радиуса
на окружности достаточно большого
радиуса

тогда
при


Следствие из леммы Жордана:

39. Вычисление определенных интегралов с помощью вычетов.
 -
определенный интеграл
-
определенный интеграл





40. Определение преобразования Лапласа.
Изображением
оригинала
 называется функция
называется функция
 комплексного переменного
комплексного переменного
 ,
определяемая интегралом
,
определяемая интегралом
 .
.
Операцию перехода от оригинала к изображению называют преобразованием Лапласа.
41. Свойства оригинала.
Функция называется оригиналом, если она удовлетворяет следующим условиям:
 при
при
- кусочно-непрерывная при
 ,
т.е. она непрерывна или имеет точки
разрыва 1-го рода, причем на каждом
конечном промежутке оси t
таких точек лишь конечное число.
,
т.е. она непрерывна или имеет точки
разрыва 1-го рода, причем на каждом
конечном промежутке оси t
таких точек лишь конечное число.Существуют такие числа
 и
и
 ,
что для всех t
выполняется неравенство
,
что для всех t
выполняется неравенство
 , т.е. при возрастании t
функция
может возрастать не быстрее некоторой
показательной функции. Число
, т.е. при возрастании t
функция
может возрастать не быстрее некоторой
показательной функции. Число
 называется показателем роста
.
называется показателем роста
.
42. Теорема линейности, смещения, подобия.
Линейной
комбинацией оригиналов соответствует
такая же линейная комбинация изображений,
т.е. если
 ,
,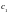 и
и
 - постоянные числа, то
- постоянные числа, то

Используя свойства интеграла, находим

Если
 ,
,
 ,
то
,
то
 ,
т.е. умножение аргумента оригинала на
положительное число
,
т.е. умножение аргумента оригинала на
положительное число
 приводит к делению изображения и его
аргумента на это число.
приводит к делению изображения и его
аргумента на это число.
По формуле имеем

(так как безразлично, какой буквой обозначена переменная интегрирования).
Если
,
 ,
то
,
то
 ,
т.е. умножения оригинала на функцию
,
т.е. умножения оригинала на функцию
 влечет за собой смещение переменной
влечет за собой смещение переменной
 .
.
В силу формулы имеем

43. Дифференцирование оригинала.
Если
и функции
 являются оригиналами, то
являются оригиналами, то

По определению изображения находим

Итак,
 .
Пользуясь полученным результатом,
найдем изображение второй производно
.
Пользуясь полученным результатом,
найдем изображение второй производно :
:

Аналогично
найдем изображение третьей производной
 :
:
 .
.
Применяя формулу
 раз,
получим формулу
раз,
получим формулу
 .
.
44. Интегрирование оригинала.
Если
,
то
 ,
т.е. интегрирование оригинала от 0 до t
соответствует деление его изображения
на
.
,
т.е. интегрирование оригинала от 0 до t
соответствует деление его изображения
на
.
Функция
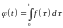 является оригиналом (можно проверить).
Пусть
является оригиналом (можно проверить).
Пусть
 .
Тогда по свойству дифференцирования
оригинала имеем
.
Тогда по свойству дифференцирования
оригинала имеем
 (так как
(так как
 ).
А так как
).
А так как
 ,
то
,
то
 .
Отсюда
.
Отсюда
 ,
т.е.
,
т.е.
45. Теорема запаздывания.
Если
,
 , то
, то
 , т.е. запаздывание оригинала на
положительную величину
, т.е. запаздывание оригинала на
положительную величину
 приводит к уменьшению изображения
оригинала без запаздывания на
приводит к уменьшению изображения
оригинала без запаздывания на
 .
.
Положив
 ,
получим
,
получим

46. Дифференцирование изображения.
Если , то

т.е.
дифференцирование изображения
соответствует умножение его оригинала
на
 .
.
47. Интегрирование изображения.
Если
и интеграл
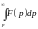 сходится, то
сходится, то
 ,
т.е интегрирование изображения от
до
,
т.е интегрирование изображения от
до
 соответствует деление его оригинала
на
соответствует деление его оригинала
на
 .
.
Используя формулу и изменяя порядок интегрирования, получаем

48. Свертка оригиналов. Интеграл Дюамеля.
Если
 и
и
 также является оригиналом, то
также является оригиналом, то
 .
.
Формула называется формулой Дюамеля.
На основании свойства переместительности свертки формулу Дюамеля можно записать в виде

Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
49. Формула Меллина.
Общий
способ определения оригинала по
изображению дает обратное преобразование
Лапласа (формула обращения Римана-Меллина),
имеющее вид
 ,
где интеграл берется вдоль любой прямой
,
где интеграл берется вдоль любой прямой
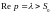 .
.
При
определенных условиях интеграл
вычисляется по формуле
 .
.
50. Решение дифференциальных уравнений операционным методом.
Пусть
требуется найти частное решение линейного
дифференциального уравнения с постоянными
коэффициентами
 ,удовлетворяющее
начальным условиям
,удовлетворяющее
начальным условиям
 где
где
 - заданные числа.
- заданные числа.
Будем
считать, что искомая функция
 вместе с ее рассматриваемыми производными
и функция
являются оригиналами.
вместе с ее рассматриваемыми производными
и функция
являются оригиналами.
Пусть
 и
и
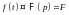 .
Пользуясь свойствами дифференцирования
оригинала и линейности, перейдем в
уравнении
от
оригиналов к изображениям:
.
Пользуясь свойствами дифференцирования
оригинала и линейности, перейдем в
уравнении
от
оригиналов к изображениям:
 .
.
Полученное уравнение называют операторным (или уравнением в изображениях). Разрешим его относительно Y:
 т.е.
т.е.
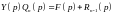 ,
где
,
где
 и
и
 - алгебраические многочлены от
степени
- алгебраические многочлены от
степени
 и
и
 соответственно.
соответственно.
Из
последнего уравнения находим
 .
.
Полученное
равенство называют операторным решением
дифференциального уравнения
.
Оно имеет более простой вид, если все
начальные условия равны нулю, т.е
 .
.
В
это случае
 .
.




