Вопрос № 4 Сформулируйте и докажите условия равновесия системы сходящихся сил

Пусть на свободное твердое тело действует система сходящихся сил {F1 F2,...Fn). Сложив по правилу силового многоугольника N—1 этих сил, приведем данную систему сходящихся сил к системе двух сил (R1 Fn). Но, по первой аксиоме, две силы R1 и FN, приложенные к твердому телу, эквивалентны нулю, т.е. находятся в равновесии только в том слу­чае, когда они имеют равные модули и направлены по одной прямой в противоположные стороны, т.е. если их равнодействующая R =R₁+Fn равна нулю. Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этой системы сил равнялась нулю, т.е. Это векторное условие равновесия системы сходящихся сил.

Т ак как равнодействующая R* изображается вектором, замы­кающим силовой многоугольник, то геометрически условие равновесия системы сходящихся сил означает, что силовой многоугольник, по­строенный на векторах слагаемых сил данной системы, замкнут.

Выразим теперь это условие аналитически. Из предыдущего параграфа известно, что модуль равнодействующей системы сходящих сил определяется по формуле системы

Но при равновесии R*= О, а следовательно, равно нулю и подкоренное выражение формулы (2). Поскольку под знаком корня стоит сумма по­ложительных чисел, то R* может равняться нулю только в случае, если

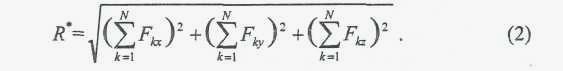
каждое из этих слагаемых равно нулю в отдельности, т.е.

Т аким образом, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические сум­мы проекций всех сил на каждую из трех выбранных любым образом координатных осей равнялись нулю.

Имея плоскую систему сходящихся сил, всегда можно плос­кость, в которой расположены силы, принять за координатную плоскость хОу. Тогда третье условие в формулах (3) выполняется тождест­венно, и условия равновесия, в рассматриваемом случае, сведутся к двум следующим условиям:

Т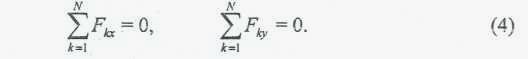 .е. для равновесия плоской системы сходящихся сил необходи­мо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из двух выбранных любым образом координатных осей, лежа­щих в плоскости действия сил данной системы, равнялись нулю.

Вопрос № 5 дайте обоснование векторной формулы момента силы относительно точки

П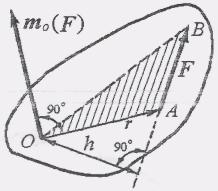 усть даны сила F, приложенная в точке А тела, и некоторый центр О. Вращательный эффект силы F относительно точки О зависит от модуля силы F и кратчайшего расстояния h от точки О до линии дей­ствия силы. Это кратчайшее расстояние h называется плечом силы от­носительно данной точки (рис. 1.13). Кро­ме того, вращательный эффект силы зави­сит от положения в пространстве плоско­сти поворота треугольника ОАВ, проходя­щей через моментную точку О и линию

действия силы F, и от направления пово­рота в этой плоскости. Для количественно­ го измерения вращательного эффекта силы F, относительно заданной точки, введем понятие момента силы. Моментом силы относительно точки называется алгебраиче­ская величина, равная произведению модуля силы на кратчайшее рас­стояние от точки до линии действия силы.Численное значение момента силы F относительно точки О бу­дем обозначать m_o(F). Тогда mo(F) = ±Fh. (1)

У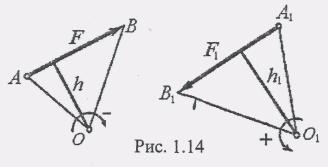 словились считать момент силы относительно точки положи­тельным, если сила стремится вращать тело вокруг заданного центра против хода часовой стрелки, и отрицательным — по часовой стрелке (рис. 1.14). Из опреде­ления величины момента силы относительно точки следует, что он не зависит от переноса силы вдоль линии ее действия и равен нулю, если линия действия силы проходит через моментную точку.

Геометрически численное значение момента силы F относи­тельно точки О выражается удвоенной площадью треугольника ОАB, вершиной которого является данная точка О, а основанием - сила F:

Момент силы относительно точки О можно принимать за ал­гебраическую величину лишь в случае плоской системы сил. О бозначим вектор-момент силы F относительно точки О сим­волом mo(F). Тогда, рассматривая его величину, определяемую форму­лами (1)-(2), и принимая во внимание направление вектор-момента, приходим к заключению, что вектор-момент m0(F) можно определить с помощью следующего векторного произведения:

Итак, момент силы относительно некоторого центра равен векторному произведению радиус-вектора точки приложения силы на вектор силы.

Вопрос № 6

Дайте обоснование определения момента силы относительно оси

Р ассмотрим тело, которое может вращаться вокруг неподвиж­ной оси z (рис. 1.16). Пусть на это тело действует сила F, приложенная к точке А тела. Проведем через точку приложения силы перпендикулярно оси z плоскость, котораяпересекается с осью z в точке О.

Разложим данную силу на две составляющие: составляющую Fz, параллельную оси z, и составляющую Fxy, лежащую в плоскости хОу и являющуюся проекцией силы F на эту плоскость. Очевидно, что со­ставляющая Fz, параллельная оси z, не может повернуть тело вокруг оси z; эта сила стремится только сдвинуть тело вдоль оси z. Это значит, что вращательный эффект силы F относительно оси z одинаков с враща­тельным эффектом, создаваемым ее составляющей Fxy (т.е. проекцией силы F на плоскость перпендикулярную оси z), относительно точки О.

Отсюда следует определение момента силы относительно оси, который будем обозначать символом mz(F).

Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикуляр­ную к данной оси, относительно точки пересечения этой плоскости с осью. Момент силы F относительно оси считается положительным, если наблюдатель, смотрящий с положительного направления оси, видит по­ворот, совершаемый составляющей Fxy силы F, происходящим против хода часовой стрелки.

Из определения момента силы относительно оси следует

Момент силы относительно оси равен нулю, если сила параллельна оси или пересекает ее. В обоих случаях сила и ось лежат в одной плоскости.

Вопрос № 7

Зависимость между моментом силы относительно оси и моментом силы относительно любой точки, лежащей на этой оси

Пусть на тело действует приложенная в точке А сила F (рис. 1.17). Момент этой силы относительно произвольной точки О, ле­жащей на оси z, перпендикулярен плоскости треугольника ОАВ и по величине равен удвоенной его площади

Проведя через точку О плоскость хОу перпендикулярно оси z и проецируя силу F на эту плоскость найдём

Т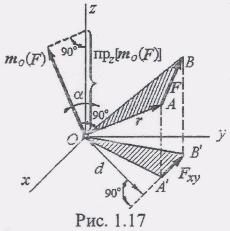 реугольник О А'В' представляет собой проекцию треугольника ОАВ на плос­ кость хОу. Известно, что площадь проекции равна площади проецируе­мой фигуры, умноженной на косинус угла между плоскостью этой фи­гуры и плоскостью проекции. Угол между плоскостями треугольников ОАВ и О А'В' равен углу между перпендикулярами к этим плоскостям, т.е. углу а между осью z и вектором mо(F) (см. рис. 1.17).

Поэтому

(3) Умножая равенстве (3) на 2 и учитывая формулы (1) и (2), находим

Таким образом, доказана следующая теорема.

Момент силы относительно оси равен проекции на эту ось вектор-момента силы относительно произвольной точки, лежащей на этой оси.

Вопрос № 8 Докажите аналитические выражения моментов силы относительно координатных осей

Е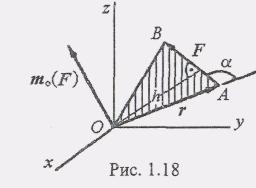 сли сила F задана своими проекциями Fx, Fy, Fz и координата­ми х, у, z точки приложения, то момент силы относительно начала ко­ординат может быть представлен в виде определителя третьего порядка*

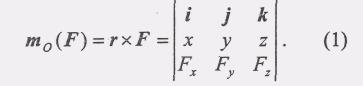
Разлагая этот определитель по элементам первой строки, найдем разло­жение вектора mo(F) по ортам декарто­вой системы координат

Коэффициенты при единичных ортах в формуле (2) равны про­екциям вектор-момента силы на оси координат.

С другой стороны, согласно теореме с связи между моментом силы относительно оси и моментом силы относительно любой точки, лежащей на этой оси проекции вектор-момента силы на оси координат, равны моментам силы относительно этих осей. Таким образом,

С помощью этих формул момент силы относительно оси можно вычислить, зная проекции силы и координаты точки ее приложения.