
- •Вопрос № 2 Докажите как система сходящихся сил приводиться к равнодействующей
- •Вопрос № 3 Дайте вывод формул для вычисления равнодействующей системы сходящихся сил
- •Вопрос № 4 Сформулируйте и докажите условия равновесия системы сходящихся сил
- •Вопрос № 9 Сформулируйте и докажите правило сложения двух параллельных сил
- •Вопрос № 18 Дайте вывод формул для аналитического определения главного вектора и главного момента произвольной пространственной системы сил
- •Вопрос № 32 Докажите как определяются координаты центра тяжести однородных тел простейшей формы (сектора, дуги окружности)
- •Другой вид трения возникает при качении одного тела по поверхности другого и называется трением качения.
Вопрос № 18 Дайте вывод формул для аналитического определения главного вектора и главного момента произвольной пространственной системы сил
Пусть дана произвольная пространственная система сил {F1,, F2,....FN). Приведем ее к заданному центру О. В результате получим, что данная система эквивалентна главному вектору и главному
![]()
Здесь по определению
![]()
Выберем декартову систему координат так, чтобы ее начало было в центре приведения. Тогда проекции главного вектора на эти оси координат определятся соотношениями:
![]()
Зная проекции главного вектора, можно определить его величину и направление по следующим формулам:
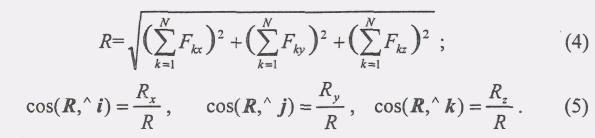
Таким же образом находим проекции главного момента:
![]()
Здесь следует помнить, что согласно теореме о связи между моментом силы относительно оси и моментом этой же силы относительно точки, лежащей на этой оси, правые части равенства (6) вычисляются как суммы моментов всех сил данной системы относительно выбранных осей координат.
Далее находим модуль и направление главного момента
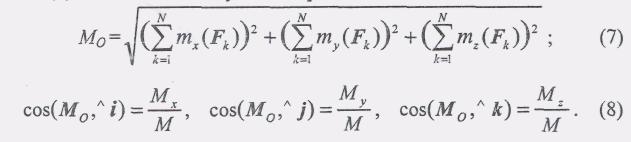
Вопрос № 19
Докажите как изменяется главный момент при изменении центра приведения
Пусть пространственная система сия приведена к центру О, т.е.
где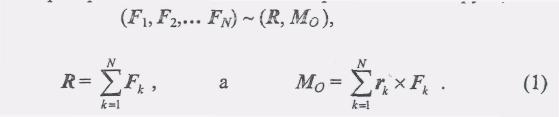
Главный момент образует с направлением главного вектора некоторый угол а (рис 1.32)
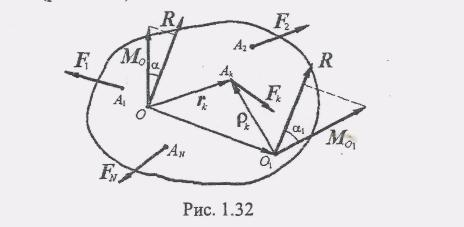
Возьмем теперь новый центр приведения О1 и приведем все силы к этому центру. В результате снова получим главный вектор, равный главному вектору R, и новый главный момент, определяемый формулой
![]()
где pк — радиус-вектор точки приложения силы Fk, проведенный из нового центра приведения О1 (см. рис. 1.32).
Главный момент Мо1 относительно нового центра приведения
изменился и теперь образует с направлением главного вектора R некоторый угол а1. Установим связь между моментами Мо и Мо1 .
Из рисунка 1.32 видно, что
![]()
(3) Подставляя (3) в равенство (2), получим
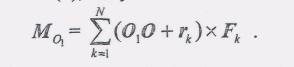 (4)
(4)
Далее, раскрывая скобки в правой части равенства (4) и вынося общий множитель О1О за знак суммы, имеем
Первая сумма в равенстве (5) равна М0, вторая - R, тогда
М01 = M0+O1O*R (6)
Второе слагаемое равно моменту главного вектора R относительно нового центра приведения в предположении, что главный вектор приложен в старом центре О, т.е.
O1O*R=mO1(R0).
Таким образом, мы доказали следующую теорему:
М01= M0+m01(R0).
Главный момент системы сил относительно нового центра приведения O1 равен сумме главного момента относительно старого центра приведения О и момента главного вектора относительно нового центра в предположении, что он приложен в старом центре О.
Следствие 1. Если главный вектор данной системы сил равен нулю, то главный момент не зависит от выбора центра приведения,
Следствие 2. Если главный вектор равен нулю и существует точка, относительно которой главный момент равен нулю, то главный момент будет равен нулю относительно любого другого центра приведения.
Следствие 3. Главный момент данной системы сил одинаков для всех точек прямой, параллельной главному вектору.
Вопрос №20. Дайте определение первого инварианта произвольной пространственной системы сил и докажите что является вторым инвариантом, как его аналитически вычислить и каков его геометрический смысл?
Величины, которые не изменяются при каком-либо преобразовании, называются инвариантными по отношению к этому преобразованию. Рассмотрим систему сил (F1, F2,…, FN) и приведем эту систему к заданному центру О. В результате получим
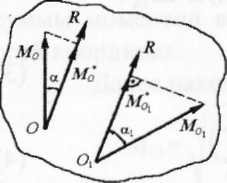
I1=R +R +R (2)
Что касается главного момента, то его модуль и направление изменяются с изменением центра приведения. Известно, что М01 =M0+O1OхR. (3)
Умножим это равенство скалярно на R: М01 * R = М0 R + (O1OхR)* R . (4)
Второе слагаемое правой части равенства (4) равно нулю как смешанное произведение коллинеарных векторов.
Поэтому M01*R = M0*R, (5)
т.е. скалярное произведение главного момента произвольной пространственной системы сил на главный вектор той же системы не зависит от выбора центра приведения и является вторым инвариантом I2 = М0 * R , (6)
или, в проекциях на оси декартовой системы координат, I2=MxRx+MyRy+MzRz. (7)
Второму инварианту можно дать очень простую геометрическую интерпретацию. На основании определения скалярного произведения I2=M0*R=M0Rcos(Mo,^ R). (8)
Откуда M0cos(Mo,^R)= I2/корень(I1) (9)
Таким образом, при R =/= 0 проекция главного момента на направление главного вектора не зависит от выбора центра приведения.
Вопрос №21. Доказать общий случай приведения произвольной пространственной системы сил к динамическому винту.
Совокупность силы, равной главному вектору, и пары сил с моментом, равным главному моменту, коллинеарным главному вектору, называется динамическим винтом или динамой.
Пусть в произвольном центре О система сил приведена к главному вектору R и главному моменту М0.
Разложим главный момент М0 на две составляющие (рис. 1.34), направленные по главному вектору и перпендикулярно к нему:
М0 = М* + М1. (I)
В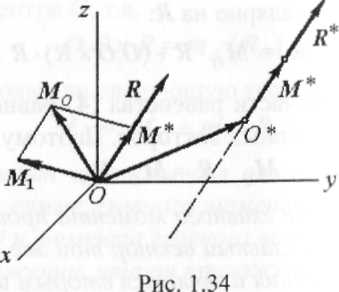 еличина
вектора М*,
равная
проекции главного момента на
направление
главного вектора, не зависит от выбора
центра приведения,
т.е.
еличина
вектора М*,
равная
проекции главного момента на
направление
главного вектора, не зависит от выбора
центра приведения,
т.е.
М* = const,
причем численно
С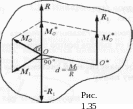 изменением центра приведения будет
изменяться только пендикулярная
составляющая М1.
Мы
всегда можем найти такой центр приведения
О*,
чтобы
переменная составляющая М1 обратилась
в нуль.Тогда главный момент и главный
вектор будут коллинеарны, а вектор М*0
будет иметь минимальную величину,
определяемую формулой (2). Составляющая
М1 представляет собой момент пары сил,
плоскость которой перпендикулярна М1
(рис. 1.35) Выберем силы R1
и –R1,
состовляющие эту пару,равны по модулю
главному вектору R
и приложим силу –R1к
центру приведения О. Система сил R
и
–R1
приложенная
к точке О,
как
эквивалента нулю может быть отброшена.
Так как момент М*
-
вектор свободный, то его можно перенести
из точки О
в
О*
. Таким
образом, заданная система сил приведена
в центре О*
к
одной силе R1
= R
и
к паре сил с моментом М*,то есть мы
получили динамический винт.
изменением центра приведения будет
изменяться только пендикулярная
составляющая М1.
Мы
всегда можем найти такой центр приведения
О*,
чтобы
переменная составляющая М1 обратилась
в нуль.Тогда главный момент и главный
вектор будут коллинеарны, а вектор М*0
будет иметь минимальную величину,
определяемую формулой (2). Составляющая
М1 представляет собой момент пары сил,
плоскость которой перпендикулярна М1
(рис. 1.35) Выберем силы R1
и –R1,
состовляющие эту пару,равны по модулю
главному вектору R
и приложим силу –R1к
центру приведения О. Система сил R
и
–R1
приложенная
к точке О,
как
эквивалента нулю может быть отброшена.
Так как момент М*
-
вектор свободный, то его можно перенести
из точки О
в
О*
. Таким
образом, заданная система сил приведена
в центре О*
к
одной силе R1
= R
и
к паре сил с моментом М*,то есть мы
получили динамический винт.
Точка О не единственная, в которой система приводится к динаме. В самом деле, силу R можно переносить вдоль линии ее действия, момент же пары сил есть вектор свободный. Следовательно, система сил может быть приведена к динаме во всех точках прямой, проходящей через центр приведения О* и являющейся линией действия главного вектора R1 = R.
Геометрическое место центров приведения, относительно которых главный момент коллинеарен главному вектору, называется центральной осью данной системы сил.
Так как на центральной оси главный момент имеет минимальное значение, эта ось называется осью наименьших главных моментов.
Найдем теперь уравнение центральной оси. Пусть О* точка центральной оси. Тогда
М*= M0+О*OхR= Мо-ОО*хR. (3)
Условие коллинеарности главного вектора и главного момента для точки О* записываем следующим образом:
M* = pR. (4)
Здесь р - постоянная величина, имеющая размерность длины, называемая параметром винта.
Т.к. величина минимального момента М* определяется формулой (2), то
Очевидно, что знак параметра определяется знаком второго инварианта. При р > 0, R и М* направлены в одну сторону.
Подставляя в формулу (4) значение минимального момента М* из (3), получим
M0-ОO*xR =pR. (6)
Таким образом нами получено уравнение центральной оси в векторной форме, причем текущей координатой является вектор ОО*. Если координаты векторов М0, R и ОО* обозначить
Мо(МX ,Му, Мz ), R(RX, Ry Rz:), OO*(х, у, z), то в проекциях на оси координат уравнение центральной оси примет вид
P
Мх – (yRz - zRy) Му - (zRx - xRz) Mz - (xRy - yRx)
Rx Ry Rz
Итак, всякая система сил, действующая на твердое тело, для которой второй инвариант не равен нулю, приводится к динаме.
Вопрос № 22
Доказать частные случаи приведения произвольной пространственной системы сил к равнодействующей и к паре
Приведение к равнодействующей
Если![]() ,
то система сил приводится к
,
то система сил приводится к
о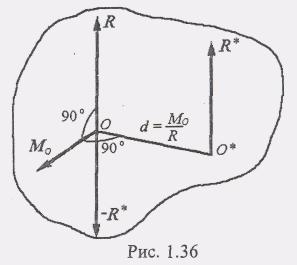 дной
силе, т.е. к равнодействующей, равной
главному вектору системы сил. Это
следует из того, что при.
дной
силе, т.е. к равнодействующей, равной
главному вектору системы сил. Это
следует из того, что при.![]() главный
вектор и главный момент взаимно
перпендикулярны (рис. 1.36), а следовательно,
минимальный момент М* = 0, и динама
вырождается в одну силу, т.е.
равнодействующую. Поясним это более
наглядно. Заменим главный момент Мо
парой сил так, чтобы силы, составляющие
эту пару, по величине были бы равны
главному вектору R. Расположим эту
пару так, чтобы одна из сил была бы
приложена в центре приведения и
направлена в сторону, противоположную
направлению R. Система сил (R и —R* )
эквивалентна нулю. Остается одна сила
R* , приложенная в
главный
вектор и главный момент взаимно
перпендикулярны (рис. 1.36), а следовательно,
минимальный момент М* = 0, и динама
вырождается в одну силу, т.е.
равнодействующую. Поясним это более
наглядно. Заменим главный момент Мо
парой сил так, чтобы силы, составляющие
эту пару, по величине были бы равны
главному вектору R. Расположим эту
пару так, чтобы одна из сил была бы
приложена в центре приведения и
направлена в сторону, противоположную
направлению R. Система сил (R и —R* )
эквивалентна нулю. Остается одна сила
R* , приложенная в
точке
О*, причем
![]() При приведении системы сил к центру О
При приведении системы сил к центру О
может
оказаться более простой случай,
когда![]() Ясно,
что в этом случае система сил эквивалентна
главному вектору, т.е. равнодействующей,
приложенной в центре приведения.
Ясно,
что в этом случае система сил эквивалентна
главному вектору, т.е. равнодействующей,
приложенной в центре приведения.
Таким
образом, чтобы система сил имела
равнодействующую, необходимо и достаточно
выполнение двух условий:![]() для
любого центра приведения.
для
любого центра приведения.
Приведение к паре сил
Если![]() то
главный момент не зависит от выбора
центра приведения. Система сил при этом
приводится к паре с моментом Мо.
то
главный момент не зависит от выбора
центра приведения. Система сил при этом
приводится к паре с моментом Мо.
Вопрос № 23
Сформулируйте и докажите теорему Вариньона для произвольной пространственной системы сил.
Если произвольная система сил имеет равнодействующую, то момент этой равнодействующей относительно любого центра равен геометрической сумме моментов всех сил этой системы относительно того же центра.
Пусть
некоторая система сил (F1, F2,...FN) приведена
к равнодействующей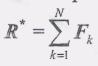 ,
приложенной в точке О*. Перенесем эту
равнодействующую в произвольную
точку О. При этом добавится присоединенная
пара с моментом
,
приложенной в точке О*. Перенесем эту
равнодействующую в произвольную
точку О. При этом добавится присоединенная
пара с моментом
![]() (1)
(1)
С другой стороны, точку О можно рассматривать как новый центр приведения главный момент относительно которого
![]() (2)
(2)
Сравнивая равенства (1) и (2), получаем теорему Вариньона
![]()
Проецируя обе части этого равенства на любую ось, проходящую через центр О, найдем, что теорема Вариньона справедлива для моментов данной системы относительно оси.
Вопрос № 24
Сформулируйте и докажите условия равновесия произвольной пространственной системы сил
Рассмотрим произвольную пространственную систему сил, действующих на твердое тело. Приведем эту систему сил к заданному центру и остановимся на том случае, когда главный вектор и главный момент данной системы сил равны нулю, т.е.
(1)
![]()
Такая система сил эквивалентна нулю, т.е. уравновешена. Следовательно, равенства (1) являются достаточными условиями равновесия. Но эти условия также и необходимы, т.е. если система сил находится в равновесии, то равенства (1) также выполняются.
В
самом деле, если бы система находилась
в равновесии, но, например![]() то
данная система привилась бы к равнодейст-
то
данная система привилась бы к равнодейст-
вующей
в центре приведения и равновесия не
было бы. Если бы![]() но
Мо =**О, данная система привилась бы к
паре и равновесия также не было пара
не могут уравновесить друг друга. Таким
образом, мы
доказали, что для равновесия произвольной
пространственной системы сил необходимо
и достаточно, чтобы главный вектор и
главный момент этой системы относительно
произвольно выбранного центра
приведения
равнялись нулю.
но
Мо =**О, данная система привилась бы к
паре и равновесия также не было пара
не могут уравновесить друг друга. Таким
образом, мы
доказали, что для равновесия произвольной
пространственной системы сил необходимо
и достаточно, чтобы главный вектор и
главный момент этой системы относительно
произвольно выбранного центра
приведения
равнялись нулю.
Условия (1) называются условиями равновесия в векторной форме. Для получения более удобной для практических целей аналитической формы условий равновесия спроецируем равенства (1) на оси декартовой системы координат. В результате получим:
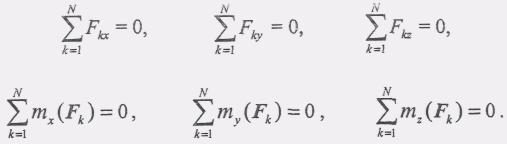 (2)
(2)
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси координат х, у и z, а также сумма моментов всех сил относительно этих же осей равнялись нулю.
Вопрос №25 Сформулируйте и докажите условия равновесия произвольной плоской системы сил
Если
все силы, действующие на твердое тело,
лежат на одной плоскости, выберем
систему координат хОу в плоскости
действия сил (рис. 1.39). В этом случае
обнаружим, что![]()
Д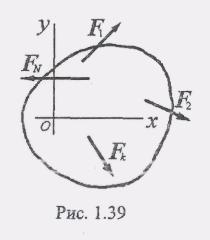 алее,
вспомнив определение момента силы
относительно оси, замечаем, что сумма
моментов всех сил относительно оси z
равна алгебраической сумме моментов
этих сил относительно, начала
координат, т.е. точки О. В результате
останутся следующие три аналитические
условия равновесия:
алее,
вспомнив определение момента силы
относительно оси, замечаем, что сумма
моментов всех сил относительно оси z
равна алгебраической сумме моментов
этих сил относительно, начала
координат, т.е. точки О. В результате
останутся следующие три аналитические
условия равновесия:
![]()
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей х и у и сумма моментов всех сил относительно любой точки, лежащей в плоскости действия сил, были равны нулю.
Читателю рекомендуется рассмотреть самостоятельно случаи плоской системы сходящихся и параллельных сил.
Вопрос № 26
Сформулируйте и докажите условия равновесия системы параллельных сил в пространстве
П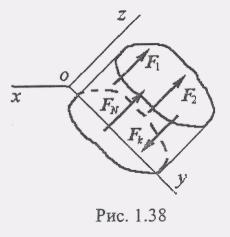 усть
на твердое тело действует пространственная
система параллельных сил. Так как
выбор осей произволен, можно выбрать
систему координат так, чтобы одна
из осей была параллельна силам, а две
другие им перпендикулярны (рис. 1.38). При
таком выборе координатных осей проекции
каждой из сил на оси х и у и их моменты
относительно оси z всегда будут равны
нулю. Это означает,что
усть
на твердое тело действует пространственная
система параллельных сил. Так как
выбор осей произволен, можно выбрать
систему координат так, чтобы одна
из осей была параллельна силам, а две
другие им перпендикулярны (рис. 1.38). При
таком выборе координатных осей проекции
каждой из сил на оси х и у и их моменты
относительно оси z всегда будут равны
нулю. Это означает,что
![]()
Эти равенства тождественно выполняются, независимо от того, находится ли данная система сил в равновесии или нет, т.е. перестают быть условиями равновесия. Поэтому в качестве условий равновесия останутся следующие:
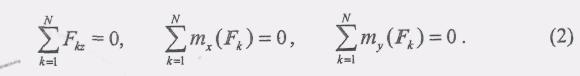
Таким образом, для равновесия системы параллельных сил в пространстве необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную этим силам, равнялась нулю и чтобы сулима их моментов относительно каждой из двух координатных осей, перпендикулярных силам, также равнялись нулю.
Вопрос № 27
Сформулируйте и докажите вторую форму условий равновесия произвольной плоской системы сил (теорема о трех моментах)
Для
равновесия произвольной плоской системы
сил необходимо и достаточно, чтобы
суммы моментов всех сил относительно
любых трех точек, не лежащих на одной
прямой, были равны нулю, т.е.:
![]() (3)
(3)
Необходимость этих условий очевидна, т.к. если плоская система сил находится в равновесии, то выполняется первая форма условий равновесия (2). А тогда из последнего равенства (2) следует, что сумма моментов всех сил относительно любой точки, следовательно, и точек А, В, С равняется нулю, т.е. выполняются условия (3).
Достаточность условий (3) следует из того, что если выполняются условия (3), а данная система сил не находится в равновесии, то она должна была бы приводиться к равнодействующей, одновременно проходящей через точки А, В, С. Это невозможно, т.к. точки А, В, С не лежат на одной прямой. Следовательно, если выполняются условия (3), то имеет место равновесие.
Вопрос № 28
Сформулируйте и докажите третью форму условий равновесия произвольной плоской системы сил.
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех этих сил относительно двух любых точек А и В и сумма их проекций на ось Ох, не перпендикулярную прямой, проходящей через точки А и В, были равны нулю:
 (3)
(3)
Н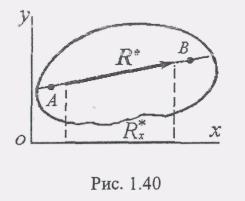 еобходимость
этих условий, так же как и в предыдущем
случае, следует из первой формы
условий равновесия. Докажем их
достаточность, т.е. докажем, что если
выполняются условия (3), то рассматриваемая
система находится в равновесии.
Выполнение первых двух условий (3)
означает, что главный момент данной
системы сил относительно центров
приведения А и В равен нулю. Такая
система может иметь равнодействующую,
приложенную в центре приведения, и
при R*=**
0 линия действия равнодействующей
проходит через точки А и В. Но по третьему
условию из (3) проекция равнодействующей
на ось Ох равна нулю. Так как ось Ох
(рис. 1.40) не перпендикулярна АВ, то
это последнее условие может быть
выполнено только в случае, если R*=0,
т.е. когда рассматриваемая система сил
уравновешена.
еобходимость
этих условий, так же как и в предыдущем
случае, следует из первой формы
условий равновесия. Докажем их
достаточность, т.е. докажем, что если
выполняются условия (3), то рассматриваемая
система находится в равновесии.
Выполнение первых двух условий (3)
означает, что главный момент данной
системы сил относительно центров
приведения А и В равен нулю. Такая
система может иметь равнодействующую,
приложенную в центре приведения, и
при R*=**
0 линия действия равнодействующей
проходит через точки А и В. Но по третьему
условию из (3) проекция равнодействующей
на ось Ох равна нулю. Так как ось Ох
(рис. 1.40) не перпендикулярна АВ, то
это последнее условие может быть
выполнено только в случае, если R*=0,
т.е. когда рассматриваемая система сил
уравновешена.
Вопрос № 29 Дайте определение центра параллельных сил и докажите формулы для определения его радиус-вектора и координат
Точка С, через которую проходит линия действия равнодействующей системы параллельных сил, при любых поворотах этих сил около фиксированных их точек приложения в одну и ту же сторону и на один и тот же угол, называется центром параллельных сил.
Н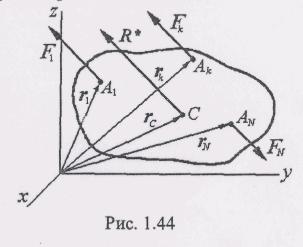 айдем
теперь координаты центра системы
параллельных сил (F1 F2,...FN) (рис. 1.44).
Радиус-векторы точек приложения сил
обозначим через rk (k = 1, 2, 3.....N), а
радиус-вектор центра параллельных сил
С обозначим через rc. Выберем одно из
возможных направлений параллельных
сил за положительное. Единичный вектор
этого направления обозначим е°, а
проекции сил на направление вектора
е° обозначим Fk. Тогда (2)
айдем
теперь координаты центра системы
параллельных сил (F1 F2,...FN) (рис. 1.44).
Радиус-векторы точек приложения сил
обозначим через rk (k = 1, 2, 3.....N), а
радиус-вектор центра параллельных сил
С обозначим через rc. Выберем одно из
возможных направлений параллельных
сил за положительное. Единичный вектор
этого направления обозначим е°, а
проекции сил на направление вектора
е° обозначим Fk. Тогда (2)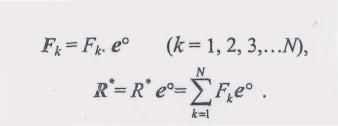 (3)
(3)
(4)По
теореме Вариньона![]()
Далее, используя предыдущие равенства (2) и (3), получим
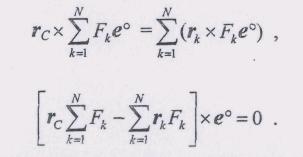
(5)
или
(6)
Так как по определению центра параллельных сил соотношение (6) удовлетворяется при любом направлении единичного вектора е°, то первый множитель в равенстве (6) должен быть равен нулю, т.е.
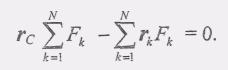 (7)
(7)
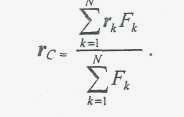 Откуда
Откуда
Проецируя обе части этого равенства на оси координат, получаем формулы для координат центра системы параллельных сил:
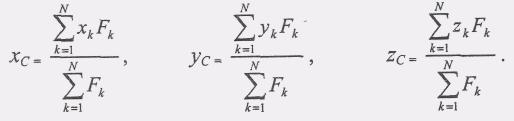 (9)
(9)
Вопрос № 30
Докажите, как определяются координаты центра тяжести однородных тел (объёма, площади, линии)
Предположим, что требуется найти положение центра тяжести однородного тела. Тело называется однородным, если его удельный вес у постоянный. В этом случае
![]() (1)
(1)
Подставив эти значения dp и Р в формулы для определения координат неоднородного тела и сокращая на у, получим :
![]() (2)
(2)
Из этих формул следует, что положение центра тяжести однородного тела не зависит от физических свойств его вещества, а зависит лишь от геометрической формы и размеров. Поэтому говорят, что формулы (2) определяют координаты центра тяжести объема.
Центр тяжести площади
В
ряде случаев тело можно считать тонкой
пластинкой или оболочкой. Предполагая,
что вес элемента его поверхности
пропорционален площади этого
элемента, т.е.![]() при у1 = const можно найти
при у1 = const можно найти
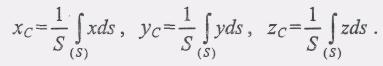 (3)
(3)
Ц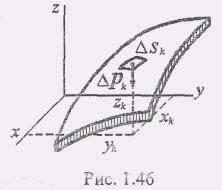 ентр
тяжести тонкой однородной оболочки
называют центром тяжести поверхности
или площади (рис. 1.46). Как следует из
формул (3), вычисление координат центра
тяжести площади связано с вычислением
интегралов по поверхности.
ентр
тяжести тонкой однородной оболочки
называют центром тяжести поверхности
или площади (рис. 1.46). Как следует из
формул (3), вычисление координат центра
тяжести площади связано с вычислением
интегралов по поверхности.
Центр тяжести линии
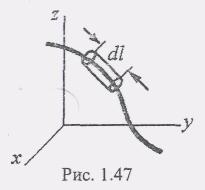
Рассмотрим
однородный криволинейный стержень с
постоянной площадью поперечного
сечения (рис. 1.47). Предположим, что вес
стержня и его элемента пропорционален
его длине, т.е.![]() Тогда формулы для координат центра
тяжести однородного стержня имеют вид:
Тогда формулы для координат центра
тяжести однородного стержня имеют вид:
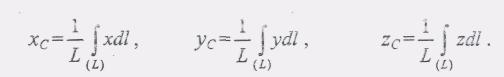
 (4)
(4)
Интегралы, стоящие в числителях формул (4) - криволинейные. Положение центра тяжести однородного стержня не зависит от его поперечных размеров, поэтому говорят, что формулы (4) определяют центр тяжести линии.
В заключение следует отметить, что определение центра тяжести однородных тел, имеющих плоскость, ось или центр симметрии, облегчается, т.к. центр тяжести таких тел лежит, соответственно, или в плоскости, или на оси, или в центре симметрии.
