
- •1.Основные действия над матрицами,свойства.
- •Операция умножения матриц
- •2. Обратимые и обратные матрицы. Условие обратимости матрицы.
- •3.Формула обратной матрицы.
- •4. Определителем n-го порядка
- •5. Свойства определителей.
- •6. Системы линейных уравнений. Элементарные преобразования систем линейных уравнений.
3.Формула обратной матрицы.
Пример
2.10. Для матрицы 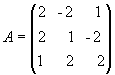 найти
обратную.
найти
обратную.
Решение. Находим
сначала детерминант матрицы А
 значит,
обратная матрица существует и мы ее
можем найти по формуле:
значит,
обратная матрица существует и мы ее
можем найти по формуле:  ,
где Аi j (i,j=1,2,3)
- алгебраические дополнения элементов
аi jисходной
матрицы.
,
где Аi j (i,j=1,2,3)
- алгебраические дополнения элементов
аi jисходной
матрицы. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
откуда  .
.
4. Определителем n-го порядка
 .
(4.3)
.
(4.3)
![]() ,
(4.4)
,
(4.4)
Определителем n-го
порядка, соответствующим матрице (4.3),
называется алгебраическая сумма n!
членов вида (4.4). Для записи определителя
употребляется символ или
det A=
или
det A=  (детерминант,
или определитель, матрицы А).
(детерминант,
или определитель, матрицы А).
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d
= ai 1 Ai
1 +
ai 2 Ai
2 +...
+ ai n Ai
n
(i = ![]() )
)
или j- го столбца
d = a1 j A1 j + a2 j A2 j +... + an j An j (j = ).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
5. Свойства определителей.
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j= ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
6. Системы линейных уравнений. Элементарные преобразования систем линейных уравнений.

относительна неизвестных x1, x2, ..., xn-1, xn называется системой линейных алгебраических уравнений.
Числа aij — коэффициенты системы, bi— правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.
Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.
Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.
Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.
Если среди правых частей bi системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.
Если все правые части системы равны нулю, то система называется однородной.
Система линейных уравнений может быть записана в матричной форме A·x = b:

Здесь A — матрица системы, b — правая часть системы , x— искомое решение системы.
Иногда удобно записывать систему линейных уравнений в другой матричной форме:
A(1)x1 + A(2)x2 + ... + A(n)xn = b. Здесь A(1), A(2), ... , A(n) — столбцы матрицы системы.

Матрица Ap называется расширенной матрицей системы.
Если исследуется неоднородная система A·x = b, b ≠ 0, то система A·x =0 называется приведенной однородной системой для системы A·x = b.
Перестановка уравнений системы, прибавление к одному уравнению системы другого уравнения, умножение уравнения на число, отличное от нуля — такие преобразования системы называются элементарными преобразованиями системы.
Элементарные преобразования приводят к эквивалентным системам.
7.Метод Гаусса.
|
|
1 шаг: а) первую строку не меняем б) из второй вычитаем первую, умноженную на 2 в) третью не меняем, т.к. там неизвестное х1 и так отсутствует. 2 шаг: а) вторую строку делим на - 4 б) из третьей строки вычитаем новую вторую (поделенную на -4). 3 шаг: делим третью строку на (-7/4). Последней матрице соответствует система.
|
или х3 = -2 + 10/7х4 + 3/7х5 х2 = -7/4х3 + 1/2х4 + 7/4х5 + 5/2 = -7/4(-2 + 10/7х4 + 3/7х5) + 1/2х4 + 7/4х5 + 5/2 = 7/2 – 5/2х4 – 3/4х5 + 1/2х4 +7/4х5 + 5/2 = 6 – 2х4 + х5 х1 = 7 – 2х2 – 4х3 + х4 + 3х5 = 7-2(6 – 2х4 + х5) – 4(-2 + 10/7х4 + 3/7х5) + х4 +3х5 = 7 – 12 + 4х4 – 2х5 + 8 – 40/7х4 – 12/7х5 + х4 + 3х5 = 3 – 5/7х4 – 5/7х5 Придавая х4 и х5 произвольные значения, например, х4 =х5 = 0, получаем решение системы, х1 =3, х2 =6, х3 =-2, х4 =0, х5 =0. |
В случае треугольной системы из последнего уравнения находим хn = bn, затем хn-1 и так далее, то есть система является совместной и определенной. Если же мы получим ступенчатую систему, то часть неизвестных будут свободными и мы будем придавать им произвольные значения. Такая система является совместной и неопределенной. Итак, ответ на вопрос о совместности системы может быть дан лишь в конце вычислений, либо этот ответ может дать теорема Кронекера - Капелли. Для того, чтобы система линейных уравнений были совместной, необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу ее расширенной матрицы, то есть
Замечание. Если ранги матрицы системы и расширенной матрицы системы равны числунеизвестных,r(А)=r(В)=n, то исходная система имеет единственное решение. Если же r(A)=r(B)<n , то система имеет бесчисленное множество решений. 8.Метод обратной матрицы. Еще один, пользующийся большой популярностью метод. Этот способ или, как его еще называеют, метод обратной матрицы называется так потому, что все решение сводится к простому матричному уравнению, для решения которого необходимо найти обратную матрицу. Для того, что бы расставить все точки над и, рассмотрим метод под микроскопом. Алгоритм решения достаточно просто. Как и в методах Гаусса и Крамера первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A-1, получим A-1AX= A-1B, откуда EX=X=A-1B. Следовательно, матрица-решение X легко находится как произведение A-1 и B. Для большей ясности решим небольшой пример методом обратной матрицы: 21x1-45x2-3.5x3=10 12x1-16x2+21x3=-16 14x1+13x2-8x3=10 Определим совместность системы уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, что бы ранг основной матрицы
и ранг расширенной матрицы
были равны. Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение. Для решения методом обратной матрицы необходимо ввести матричные обозначения
Найдем обратную матрицу A-1.
Для нахождения матрицы X умножим обратную матрицу А-1 на матрицу С
Получили решение системы уравнений X1=0.227 X2=-0.209 X3=-1.194 9.Правило Крамера. Рассмотрим систему линейных уравнений
Система трех уравнений может быть решена по правилу Крамера, рассмотренному выше для системы двух уравнений. Составим определитель из коэффициентов при неизвестных
Назовем его определителем системы. Если D≠0, то система совместна. Далее составим три вспомогательных определителя:
Решение системы (7) находим по формулам:
которые называют формулами Крамера.
Пример
6. Решить
систему уравнений Решение. Вычислим определитель системы.
Вычислим теперь вспомогательные определители:
Тогда
10.ФСР ОСЛУ Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространства Rn.Размерность этого подпространства равна n − r, где r − ранг матрицы системы A. Любой базис пространства решений однородной системы линейных уравнений называется фундаментальной системой решений однородной системы. Иначе говоря, любая упорядоченная совокупность n − r линейно независимых решений однородной линейной системы образуетфундаментальную систему решений однородной системы.
Пример
Решим систему
Перепишем её в матричном виде:
Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:
Таким
образом ранг системы
(ранг её основной матрицы) равен двум.
Это значит, что существует Перепишем полученную систему в виде уравнений:
Возьмём
Подставим
по очереди единицы в качестве одной
из свободных переменных:
Тогда общее решение рассматриваемой системы может быть записано так:
а
вектора
11.Связь решения однородной и неоднородной СЛУ. Общее решение неоднородной системы линейных уравнений равно сумме общего решения приведенной однородной системы и любого частного решения неоднородной системы. Поскольку общее решение линейной системы, записанной в каноническом виде, определяется формулами:
то общее решение неоднородной системы можно записать в векторной форме в виде:
Здесь С1, С2, ..., Сn−r−1, Сn−r — произвольные константы, r — ранг матрицы системы.
12. Определение векторного пространства. Линейной зависимости и независимости системы векторов.
Линейное,
или векторное
пространство
При этом на операции накладываются следующие условия:
Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
Система векторов e1,e2, ..., ek линейного пространства L называется линейно независимой системой, если равенство С1·e1+С2·e2+ ...+Сk· ek = 0 возможно только когда все коэффициенты С1, С2, ..., Сk равны нулю. Здесь 0 — нулевой вектор линейного пространства L, С1, С2, ..., Сk — числовые коэффициенты. Если система векторов e1,e2, ..., ek линейного пространства L не является линейно независимой системой, то она называетсялинейно зависимой системой векторов.
13. Свойства линейной зависимости векторов. Определение. Векторы называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно i , т.е. . Если же только при i = 0 выполняется , то векторы называются линейно независимыми. Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы. Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима. Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов. Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны. Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны. Свойство 6. Любые 4 вектора линейно зависимы.
14.Матрица перехода от базиса к базису.
Ма́трицей
перехо́да от базиса
Обозначается Представление Так как
Матрица перехода это
Использование
При
умножении столбца, составленного из
коэффициентов разложения вектора
по базису Из-за того, что уменьшает объём работы при переводе векторов аффинных пространств и в пространстве столбцов Rnв другие базисы, используется в трёхмерном моделировании. Пример Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить матрицу поворота на него:
15.Координаты вектора. Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
где — координаты вектора. Связь координат вектора, вычисленных в разных базисах Пусть
Нас
интересует связь между координатами
Разложим векторы базиса по базису . Получим
Тогда, если то Или
в матричной форме Заменяя
в (*) столбец Из этого равенства следует, что В
дальнейшем матрицу в случае, когда в первом экземпляре пространства выбран базис , а во втором экземпляре того же пространства выбран базис . 16.Подпространства. Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat(L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы
Последние два утверждения эквивалентны следующему:
В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными.
Пусть
Предложение
1. Пересечение
Замечание
1. Объединение
Пример
1. Пусть Определение 1. Суммой1) подпространств и называется наименьшее подпространство в , содержащее и , то есть
Вообще говоря, можно определить сумму любого конечного числа подпространств:
Определение
1'. Сумма подпространств
Предложение 2. Пусть и — подпространства конечномерного векторного пространства . Тогда
17.Формула Грассмана. Формула Грассмана — математическая формула, описывающая размерность подпространства конечномерного пространства. Выведена немецким ученым Г. Г. Грассманом. Формулировка: Если линейное пространство V конечномерно, то конечномерными будут и все линейные подпространства в V, причем, по свойству монотонности размерности, размерности подпространств не превышают размерность всего пространства. Вычисление размерности может быть сделано по формуле:
18.Линейное отображение. Лине́йным отображе́нием векторного пространства LK над полем K в векторное пространство MK (лине́йным опера́тором из LK в MK) над тем же полем K называется отображение
удовлетворяющее условию линейности f(x + y) = f(x) + f(y), f(αx) = αf(x).
для
всех
Ядром линейного
отображения
ker f является подпространством в V. Оно всегда содержит нулевой элемент пространства V. Согласно основной теореме о гомоморфизме, образ f изоморфен фактору пространства V по ядру f:
Соответственно, размерность образа пространства равна разности размерностей пространства и ядра отображения, если размерность V конечна:
а прообраз любого вектора определён с точностью до прибавления вектора из ядра:
Образом
подмножества[1]
21.Диагональный вид. 2.10. Приведение матрицы к диагональному виду Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия — A = TΛT−1 Здесь Λ = diag(λ1,..., λN) — это диагональная матрица, элементами которой являются собственные значения матрицы A, а T — это матрица, составленная из соответствующих собственных векторов матрицы A, т.е. T = (v1,...,vN). Например,
Рис. 23 Приведение к диагональному виду
|




 либо
ступенчатую
либо
ступенчатую  матрицу
системы.
матрицу
системы.
 (7)
(7) .
. ,
, ,
, .
.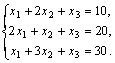
 .
Система совместна, так как D≠0.
.
Система совместна, так как D≠0. ,
,  ,
, .
.

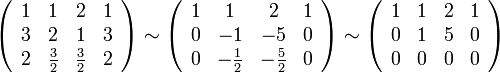

 ,
, составляют
фундаментальную систему решений.
составляют
фундаментальную систему решений.


 .
.


 . Найдем координаты образа вектора
. Найдем координаты образа вектора  .
В линейном пространстве
X4 введен
новый базис
.
В линейном пространстве
X4 введен
новый базис  .
Найдем координаты вектора X, координаты
образа Y = A X и матрицу оператора
в новом базисе.
.
Найдем координаты вектора X, координаты
образа Y = A X и матрицу оператора
в новом базисе.  .
Проверим, принадлежат ли векторы
.
Проверим, принадлежат ли векторы 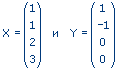 ядру
оператора, а векторы
ядру
оператора, а векторы  -
его образу.
-
его образу.  .
Запишем матрицу оператора в базисе
из собственных векторов и матрицу
перехода к собственному базису.
.
Запишем матрицу оператора в базисе
из собственных векторов и матрицу
перехода к собственному базису.
