10.2.1. Любой вектор равен сумме всех своих составляющих по осям координат.

- разложение вектора на составляющие по координатным осям.

10.2.2. Для того, чтобы задать вектор, достаточно задать все его координаты.

- задание вектора в координатной форме;

тогда - вектор единичной длины сонаправленный с , т.е.

- задание единичного вектора

в координатной форме.

10.2.3. Действия с векторами в координатной форме

Пусть векторы заданы своими координатами:

; ; ; - скаляр.

10.2.3.1.

10.2.3.2.

10.2.3.3.

10.2.3.4.

10.2.3.5.

10.2.3.6.

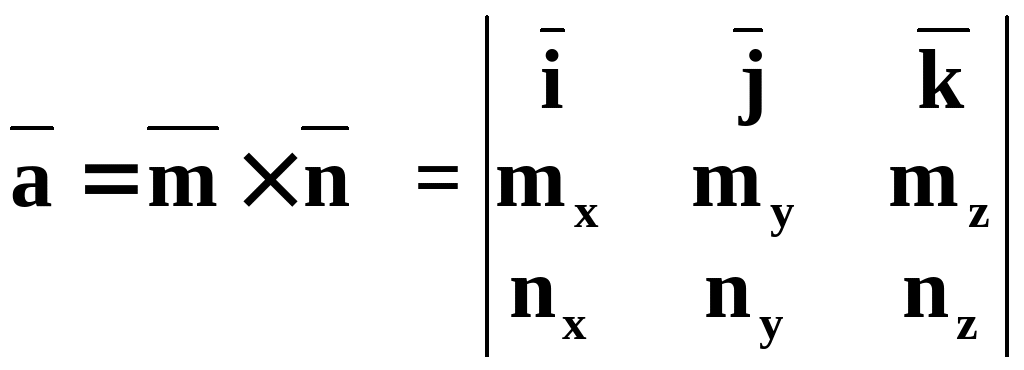
10.2.3.7. .

10.2.3.8. .

10.2.3.9. .

11. Комплексные числа

Мнимой единицей будем называть такое число ( i ), квадрат которого равен ( -1 ).

.

Мнимым числом будем называть выражение вида , где b - вещественное число, а i - мнимая единица.

Комплексным числом будем называть выражение вида , где a, b - вещественные числа, i - мнимая единица. При этом Re(z)=a называют вещественной частью числа, а Im(z)=b - мнимой частью.

Множество всех комплексных чисел назовем С.

Если a = 0, то z = bi - мнимое число; если b = 0, то будем считать, что bi = 0 , тогда z = a - вещественное число.

Комплексное число будет задано, если известна его вещественная и мнимая часть, поэтому его можно задать упорядоченной парой чисел (a, b). Упорядоченные пары чисел можно рассматривать как точки M(a, b) на координатной плоскости. При этом вещественная часть числа откладывается на оси абсцисс (ее называют вещественная ось), а мнимая - на оси ординат (ее называют мнимая ось). Если точки на координатной плоскости изображают комплексные числа, то такую плоскость называют комплексной плоскостью. Следовательно, множество всех комплексных чисел ( С ) можно рассматривать, как множество всех точек комплексной плоскости, причем ось абсцисс содержит все точки, изображающие вещественные числа, а ось ординат - чисто мнимые.

^{Мнимая ось}

b M₂ M(a, b) z = a + bi

_r

 M₁

O a ^{вещественная ось}

Полярные координаты точки М - (r, ) по отношению к комплексному числу z=a+bi обозначаются так: r = Mod(z) - модуль числа,  =Arg(z) - аргумент числа.

Модуль и аргумент связаны с вещественной и мнимой частью комплексного числа соотношениями:

.

Модуль комплексного числа можно рассматривать как длину радиус-вектора точки М(a, b), изображающей число z=a+bi, т.е. .

.

Последнее выражение в этой формуле называют тригонометрической формой комплексного числа. Отсюда следует, что комплексное число не изменится, если к аргументу прибавить слагаемое, кратное .

.

Число называют комплексным сопряженным числу z.

Можно доказать, что радиус-вектор суммы двух комплексных чисел равен сумме их радиус-векторов, а радиус-вектор разности двух чисел - разности радиус-векторов уменьшаемого и вычитаемого.

Комплексное число с модулем равным единице принято обозначать , тогда

- показательная форма записи комплексного числа.

.

Пусть дано натуральное число n и комплексные числа:

.

Условия равенства двух комплексных чисел

или

Сложение, вычитание, умножение двух комплексных чисел выполняются, как аналогичные действия с многочленами. Поэтому справедливы следующие формулы:

или

Отсюда следует, что произведение сопряженных чисел есть число вещественное, равное квадрату их модуля: .

или

Формулы умножения, деления, возведения в натуральную степень и извлечения корня, выполненные в тригонометрической форме, называют формулами Муавра.

Для модулей комплексных чисел справедливы следующие свойства:

11.1 Модуль суммы двух чисел не превосходит суммы их модулей.

11.2 Модуль разности не меньше, чем разность модулей.

11.3 Модуль произведения равен произведению модулей.

11.4 Модуль частного равен частному от деления модулей.

11.5 Модуль степени равен степени модуля.

11.6 Модуль корня равен корню той же степени из модуля.

Пусть . Тогда . Отсюда следует, что абсолютную величину вещественного числа можно рассматривать как частный случай его модуля. Поэтому все свойства модуля справедливы и для абсолютных величин.

Все числа, модули которых равны 1 изображаются точками комплексной плоскости, лежащей на окружности тригонометрического круга.

Пусть дано уравнение вида: ,

где х - переменная (неизвестна),

а₀ , а₁ , а₂ , а₃ , ... , а_n - вещественные постоянные (заданные коэффициенты).

Выражение в левой части этого равенства называют многочленом (полиномом)

n-ой степени или целой рациональной функцией, а само равенство - алгебраическим уравнением n -ой степени.

Основная теорема высшей алгебры утверждает, что такое уравнение имеет ровно n корней среди которых могут быть и одинаковые корни, причем все корни могут оказаться вещественными, возможно все корни окажутся комплексными, может быть только часть корней будут комплексными. При этом надо помнить, что если комплексное число является корнем уравнения, то сопряженное тоже обязательно является корнем.

Например, уравнение х²-2х+2 = 0 имеет два сопряженных комплексных корня x₁=1-i;

x₂=1+i.

Уравнение х³+4х = 0 имеет один вещественный корень х₁=0 и два комплексных сопряженных: x₂=i; x₃=-i.