22. Директрисы эллипса и гиперболы.

ДиректрисойD_i(i=1,2) эллипса, отвечающей фокусу F_i(i=1,2) называется прямая, расположенная в полуплоскости π_i(i=1,2) и перпендикулярная большой оси эллипса на расстоянии 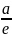от ее центра

D₁= ; D₂=

Расстояние от фокуса, до соответствующей директрисы: р=а*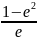

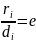
Директрисой D_i(i=1,2)гиперболы, отвечающей фокусу F_i(i=1,2) называется прямая, расположенная в полуплоскости π_i(i=1,2) и перпендикулярная действительной оси гиперболы на расстоянии от ее центра.

D₁= ; D₂=

Расстояние от фокуса, до соответствующей директрисы: р=а*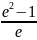

23. Эксцентриситет. Фокальный параметр.

Эксцентриситетом эллипса называется величина e=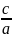

Если е=0, то эллипс превращается в окружность. Если е=1, то эллипс превращается в свою сдвоенную большую ось.

Эксцентриситет эллипса можно рассматривать как меру вытянутости эллипса

Эксцентриситетом гиперболы называется величина e=

Эксцентриситет гиперболы можно рассматривать как числовую характеристику величин угла между ее асимптотами

Прямая, проходящая через фокусы кривой называется фокальной осью. Проведем через какой-нибудь фокус кривой прямую перпендикулярную фокальной оси. Эта прямая пересекает кривую в 2 точках Р и Р`. Обозначим через 2р длину отрезка РР`.р-фокальный параметр.

1. Для окружности. р=R

2. Для эллипса р=

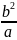
3. Для гиперболы р=

24. Уравнение эллипса, гиперболы и параболы в полярных координатах. Оптические свойства эллипса, гиперболы и параболы.

Уравнение эллипса, гиперболы и параболы в полярных координатах: ρ=

Лучи света, исходящие из одного фокуса эллипса, после зеркального отражения от эллипса проходят через другой фокус.

Лучи света, исходящие из одного фокуса гиперболы, после зеркального отражения от гиперболы кажется исходящим из другого фокуса.

Лучи света, исходящие из фокуса параболы, после зеркального отражения от параболы, образуют пучок, параллельный оси параболы.

25. Исследование формы поверхностей 2-го порядка по их каноническим уравнениям.

1. Эллипсоид

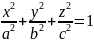
z=h 1-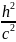

Если |h|>cто мнимый эллипс

Если |h|<cто эллипс

Если |h|=cто точка

2. Однополостный гиперболоид

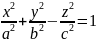
y=0

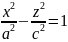– гипербола

x=0

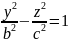– гипербола

z=h 1+ - эллипс

3. Двуполостный гиперболоид

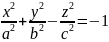
y=0

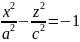– сопряженная гипербола

x=0

– сопряженная гипербола

z=h -1

Если |h|>cто в пересечении по эллипсу

Если |h|<cто не пересекает

Если |h|=cто касается

4. Конус 2 порядка

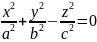
y=0

– пара пересекающихся прямых

x=0

– пара пересекающихся прямых

z=h

Если |h|>0то 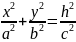- эллипс

Если |h|=0то – точка

5. Эллиптический параболоид

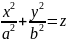
y=0

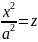– парабола

x=0

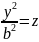– парабола

z=h

Если h>0то в пересечении по эллипсу

Если h<0то не пересекает

Если h=0то касается

6. Гиперболический параболоид

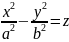
y=0

– парабола

x=0

– парабола

z=h

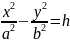
Если h>0то пересекает по гиперболе

Если h<0то пересекает по гиперболе

Если h=0то в сечении пара пересекающихся прямых

7. Эллиптический цилиндр

z=h

В сечении эллипс

8. Гиперболический цилиндр

z=h

В сечении гипербола

9. Параболический цилиндр

y²=2px

z=h

В сечении парабола