22. Линии эллиптического, гиперболического и параболического типов. Центры линий второго порядка.

Пусть на плоскости A²(i) выбран некоторый репер и задано уравнение линии второго порядка а₁₁x +2 а₁₂x₁x₂ + а₂₂x +2 а₁х₁ +2а₂х₂ + а = 0. (1)

Векторы, имеющие относительно линии (1) асимптотические направ­ления, определяются равенством а₁₁c +2 а₁₂c₁c₂ + а₂₂c = 0. (2)

Пусть вектор с имеет асимптотическое направление относительно линии (1). Так как любой вектор с, где а — произвольное, отличное от нуля комплексное число, имеет то же направление, то направление вполне определяется заданием отношения с₁ : с₂ координат вектора с, если с₂ ≠ 0. Мы будем употреблять запись с₁ : с₂ и в том случае, когда с₂ = 0, а именно: символ 1:0 задает направление базисного вектора е .

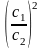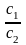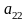Пусть а₁₁ ≠ 0. У вектора, имеющего асимптотическое направле­ние, с₂ ≠ 0, так как в противном случае из равенства (2) следует а₁₁c = 0, а а₁₁ ≠ 0 и c₁ ≠ 0. Запишем теперь равенство (2) в виде а₁₁ +2 а₁₂ + =0.

Решая это квадратное уравнение относительно c /с₂, получаем =

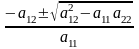
Возможны следующие случаи:

1) 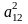- 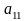< 0, поэтому не существует действительных асимптотических направлений относительно линии (1), иначе, существует два мнимых асимптотических направления;

2. - > 0, следовательно, существует два действитель­ных асимптотических направления;

3. - = 0, поэтому существует одно действительное асимптотическое направление.

Если = 0, а₂₂ ≠ 0, то, меняя ролями c и с₂, приходим к тем же случаям.

Наконец, пусть = 0 и а₂₂ = 0. Тогда а₁₂ ≠ 0, и уравнение (2) принимает вид а₁₂ c с₂ = 0. В этом случае существует два асимпто­тических направления, определяемых векторами с(1, 0) и с'(0, 1).

Определение 5.1. Линия второго порядка на плоскости A² (i) называется линией эллиптического, гиперболического или пара­болического типа в соответствии с тем, к какому из трех указанных выше случаев она относится.

При аффинных преобразованиях плоскости А²(1) линия второго порядка не может изменить свой тип, так как при этом действитель­ные асимптотические направления переходят в действительные.

23. Диаметральные плоскости. Диаметры линий второго порядка.

Пусть в пространстве Aⁿ(i) выбран некоторый репер и задана квадрика

+2 =0 (1) Пусть, далее, x =b + c t, i=1, 2, ..., п, (2) есть уравнения прямой, направляющий вектор которой с( c , c₂, ... , c ) (3) имеет неасимптотическое относительно квадрики (1) направление. Прямая (2) пересекает квадрику (1) в двух точках: М′ (x′ , x′₂,...,x′ ) и М″( x″ , x″₂,...,x″ ), быть может, совпадающих.

Определение 7.1. Отрезок М'М", определяемый двумя точ­ками, принадлежащими квадрике (1), называется хордой этой квадрики.

Если в качестве начальной точки В(b₁ ,b₂, ..., b_n) прямой (2) взять середину хорды М'М", то должно выполняться равенство (6) из §6: 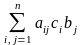+ = 0. (4)

(Если М' = М", то положим В = М' = М″.)

Рассмотрим теперь все прямые с заданным направляющим вектором (3). Середины хорд, отсекаемых на этих прямых квадри­кой (1), образуют множество точек, определяемое уравнением 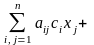+ = 0, (5)

которое получается из равенства (2) заменой обозначений b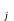 на х . Уравнение (5) —линейное. В самом деле, если в этом уравнении все коэффициенты при х_j — нули, т. е. 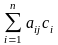= 0, j = 1, 2, … , n, то, умножая каждое из этих равенств на соответствующее с, и сум­мируя по j, получаем = 0,

т. е., вопреки предположению, вектор (3) имеет асимптотическое направление. Таким образом, верна

Теорема 7.1. Множество середин хорд, отсекаемых квадрикой (1) на всех параллельных прямых с направляющим вектором (3), имеющим неасимптотическое направление, является гиперплос­костью с уравнением (5).

Определение 7.2. Гиперплоскость (5) называется диамет­ральной гиперплоскостью квадрики (1), сопряженной с направле­нием вектора (3).

Очевидно, что диаметральная плоскость — аффинное понятие.

Диаметры линий второго порядка

Рассмотрим плоскость A²(i). Выберем некоторый репер и зададим линию второго порядка с уравнением а₁₁x +2 а₁₂x₁x₂ + а₂₂x +2 а₁х₁ +2а₂х₂ + а = 0. (1)

В этом случае диаметральная гиперплоскость является прямой и на­зывается диаметром. Уравнение диаметра, сопряженного с неасимп­тотическим направлением вектора с(с , c₂), имеет вид

(а₁₁с + а₁₂с₂)x′ + (а₁₂с₁ + а₂₂с₂)х₂ + a₁c₁ + а₂с₂ = 0. (2)

Как отмечалось в предыдущем параграфе, каждый диаметр линии (1) проходи! через любой ее центр. Для линии (1), имеющей прямую центров, вопрос о диаметрах решается теперь полностью: у такой линии имеется только один диаметр — прямая центров.

Рассмотрим теперь вопрос о диаметрах центральной линии (1). В этом случае

а₁₁а₂₂ — а ≠ 0. (3)

Определение 8.1. Два направления c :с₂ и c′ :с′₂ называются сопряженными относительно центральной линии второго порядка (1), если они удовлетворяют соотношению а₁₁с c′ + а₁₂ (с ₁c ′ + с₂с′ ) + а₂₂с₂с′₂ = 0. (4)

Отметим основные свойства сопряженных направлений.

1. Каждому направлению c :с₂ соответствует в качестве сопря­ женного одно вполне определенное направление c′ :с′₂.

► В самом деле, перепишем равенство (4) в виде

(а₁₁с + а₁₂с₂)c′ +( а₁₂с₁ + а₂₂с₂с₂ ) c′ = 0. (5)

Е сли предположить, что а₁₁ c₁ + a₁₂c₂ = 0, (6)

a_l2c₁ + a₂₂c₂ = 0.

то в силу неравенства (3) мы получим, что система уравнений (6) относительно неизвестных c и с₂ имеет только нулевое решение: c = 0, с₂ = 0. Но это невозможно, так как вектор с(c ,с₂)—ненуле­вой. Итак, оба коэффициента при c и с₂ в уравнении (5) не могут одновременно обратиться в нуль, и, следовательно, из уравнения мы найдем вполне определенное отношение c′ : с′_2.◄

2. Асимптотическое направление, и только оно, сопряжено самому себе.

► В самом деле, если для данного направления c : с₂ сопряженным является само это направление, то равенство (4) дает а₁₁с ² + 2а₁₂с₁с₂ + а₂₂с = 0 (7)

т. е. направление c : с₂ — асимптотическое.

Обратно, если направление c : с₂ — асимптотическое, т. е. удов­летворяет равенству (7), то равенство (4) выполняется, если c′ = c и с'₂ == с₂. Следовательно, направление c : с₂ сопряжено само­му себе. ◄

3. Если направление c :с₂ — неасимптотическое, то сопряженное направление также неасимптотическое и является направлением диаметра, сопряженного с направлением c :с₂.

►В самом деле, диаметр, сопряженный с неасимптотическим на­правлением c : с₂,— это прямая (2). Для направляющего вектора с'(с', с₂) этой прямой выполняется условие с′ : с'₂= — (a_l2 c + a₂₂c₂):(a₁₁ c + a₁₂c₂), откуда и следует равенство (5).◄

Определение 8.2. Два диаметра линии второго порядка, имеющие взаимно сопряженные направления, называются сопряжен­ными диаметрами.

Из определения диаметра следует, что каждый из двух сопряжен­ных диаметров делит пополам все хорды, параллельные другому диаметру.

На рис. 8.1 изображены эллипс, два его взаимно сопряженных диаметра и параллельные им хорды.

Мы знаем, что любой диаметр центральной линии второго

порядка (1) проходит через ее центр. По­кажем теперь, что

любая прямая l неасимптотиче­ского направления, проходящая рис. 8.1

через центр цен­тральной линии второго порядка, является диамет­ром этой линии. В самом деле, пусть c : с₂ определяет направление прямой / и c :с₂— сопряженное на­правление, причем оба этих направления являются неасимпто­тическими. Рассмотрим диаметр, сопряженной с направлением c : с₂. Он имеет направление c : с₂ и, проходя через центр ли­нии (1), совпадает с прямой l.

Теперь рассмотрим диаметры параболы. Пусть парабола в неко­торой ортонормированной системе координат задается уравнением 2рх₁ — х²₂ = 0. (8)

Уравнение диаметра параболы (8), сопряженного с направле­нием c : с₂, имеет вид р c — с₂х₂ = 0. Отсюда следует, что все ди­аметры параболы параллельны ее оси и любая прямая, параллельная оси параболы, является диаметром.