10. Параллельный сдвиг аффинного пространства. Формулы параллельного сдвига. Центроаффинное отображение. Формулы центроаффинного отображения.

11. Фигуры в аффинном пространстве. Простое отношение трех точек. Отрезок. Середина отрезка. Центр фигуры.

Пусть - аффинное пространство, связанное с линейным пространством над полем Р.

Определение 25.11. Фигурой в пространстве называется произвольное множество точек этого пространства.

Рассмотрим в качестве двухмерного аффинного пространства плоскость, изучаемую в элементарной геометрии. Примерами фигур в плоскости будут: пустое множество, точка, прямая, треугольник, окружность, круг, пара параллельных прямых и др. В произвольном аффинном пространстве фигурами являются: пустое множество, точка, прямая, k-мерная плоскость, пара плоскостей и т.д.

В этом параграфе будем обозначать группу всех аффинных преобразований пространства буквой G.

Определение 25.12. Фигура 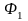пространства называется аффинно эквивалентной фигуре 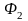этого пространства, если существует аффинное преобразование 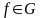, переводящее фигуру в фигуру , т.е. ( )= .

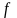Теорема 25.19. Аффинное преобразование f пространства переводит всякую k- мерную плоскость в k- мерную плоскость. Все плоскости данной размерности k в пространстве аффинно эквивалентны друг другу и образуют один аффинный класс.

Теорема 25.20. Множество всех пар плоскостей пространства ____, имеющих одну и ту же характеристику, образует класс аффинно эквивалентных фигур.

Следствие 25.2. Любое аффинное преобразование аффинного пространства 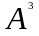переводит параллельные прямые в параллельные прямые, а параллельные плоскости в параллельные плоскости.

Далее в этом параграфе будем предполагать, что основным полем является поле R или С.

Пусть 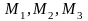-три точки пространства , принадлежащие одной прямой, причем . Тогда найдется число 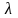из основного поля, такое, что

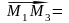
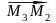
Определение 25.13. Три точки аффинного пространства , принадлежащие одной прямой, называются коллинеарными. Число , определяемое формулой (9), называется простым отношением коллинеарных точек и обозначается( ) .

Теорема 25.21. Аффинное преобразование f пространства сохраняет коллинеарность точек и простое отношение тройки коллинеарных точек.

Док-во: Пусть - - тройка коллинеарных точек пространства . Будем предполагать эти точки попарно различными, так как в противном случае утверждение теоремы очевидно. Тогда имеем равенство (9). Пусть f(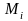 ) = 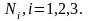. Тогда 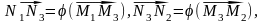где -однородная часть преобразования f. В силу линейности из равенства (9) следует равенство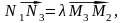 . Но это означает 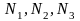, что точки коллинеарны и простое отношение тройки точек равно , т.е. простому отношению тройки точек .

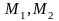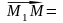
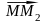Пусть _ - две произвольные точки пространства . Если эти точки различны, то через них проходит одна и только одна прямая и на этой прямой есть единственная точка М, удовлетворяющая условию (10)

Если точки совпадают, то точка М, удовлетворяющая условию (10), также существует и единственна: М= .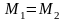

Определение 25.14. Произвольная пара точек пространства называется отрезком, а точка М, удовлетворяющая условию (10) – серединой этого отрезка.

Пусть в пространстве выбран некоторый репер (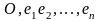 ). Тогда точки будут иметь определенные координаты: 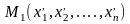, , . Равенство (10) имеет вид …+ + + +

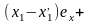
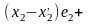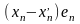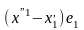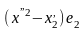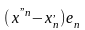
В силу линейной независимости векторов 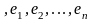имеем:

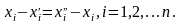
Отсюда получаем формулы для координат середины отрезка:

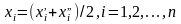
Определение 25.15. Точка М называется центром фигуры Ф , если для всякой точки 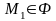существует такая точка , что точка М является серединой отрезка .