§8 Важнейшие классы сложности задач.

Класс сложности задач – совокупность тех алгоритмических задач, для которых существует хотя бы один алгоритм с теми или иными сложностными характеристиками.

Определение 1. Алгоритм называется полиномиальным , если его временная сложность в худшем случае T(n) ограничена сверху некоторым полиномом от n, т.е. T(n)=O(p(n)), где p(n)=a_mn^m+a_m-1n^m-1+…+a₁n+a₀, a_i∈ℝ, m∈ℕ.

Определение 2. Алгоритм называется экспоненциальным, если существует k∈ℝ , k ≥ 1 и существует бесконечное множество значений n∈ℕ таких, что T(n) ≥ .

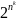На практике полиномиальность алгоритма в большинстве случаев говорит о его пригодности для решения больших задач, т.е. его «эффективности». В современной теории сложности вычислений, понятие полиноминального алгоритма является математическим уточнением интуитивного понятия «эффективный алгоритм».

«полиномиальность» = «эффективность»

Определение 3. Классом сложности P называется класс всех тех алгоритмических задач, которые допускают решение хотя бы одним полиномиальным алгоритмом.

Пример1. Бинарное отношение R на множестве М, |M|=n называется гамильтоновым, если существует упорядочение (i₁,i₂,…,i_n) элементов из М, i_j∈M, j= , такое, что

(i₁,i₂)∈R,…,(i_n-1,i_n)∈R (1)

В настоящее время неизвестно полиномиального алгоритма с временной сложностью T(n)=O(p(n)) для проверки гамильтоновости бинарного отношения R на множестве M, такого, что |M|=n.

Простейшая идея требует проверки условий (1) для n! перестановок (i₁,i₂,…,i_n) элементов из M, что превосходит по временной сложности любой полином от n.

Задачей распознавания называется задача, имеющая ответ «да» или «нет».

Практически все наиболее важные модельные задачи в теории алгоритмов и сложности вычислений допускают переформулировку в виде задач распознавания.

Определение 4. Говорят что задача распознавания П₁ полиномиально сводится к задаче распознавания П₂, если существует полиномиальная функция (алгоритм) f, перерабатывающая массивы входных данных I₁ задачи П₁ в массивы входных данных I₂=f(I₁) для задачи П₂ так, что для любого I₁ ответ в задаче П₁ совпадает с ответом в задаче П₂ для входных данных I₂=f(I₁).

Под недетерминорованным алгоритмом распознавания (Н-алгоритмом) понимают алгоритм, в котором разрешены недетерминированные операторы вида goto l₁ or l₂. Таким образом для каждого массива входных данных имеется не один, а несколько (в общем случае – экспоненциальное число) путей, по которым может развиваться вычисление.

(*) Н-алгоритм распознавания, по определению, выдает окончательный ответ «да», если существует хотя бы один путь развития вычисления, на котором выдается ответ «да», и окончательный ответ «нет» если ни на одном пути вычисления не получается ответ «да».

Н-алгоритм является математической абстракцией и, в отличие от детерминированных алгоритмов( т.е. алгоритмов, определенных с помощью формальных алгоритмических моделей – см: §1) не соответствует реально существующим вычислительным машинам.

Пусть имеется массовая задача распознавания П, частная задача p ∈ П, p имеет массив входных данных I, |I| = n, то есть |p|= n –размер задачи p.

Работа H – алгоритма над задачей p имеет 2 этапа

1. Некоторый «угадывающий модуль» недетерминированно (произвольно), генерирует путь развития вычисления («подсказку»), (например, в виде слова c(I), кодирующего направление ветвлений в операторах вида goto l₁ or l₂).

2. Детерминированно проверяется, будет ли для массива I на выбранном пути вычисления c(I) получен ответ «да».

3. Выпадает окончательный ответ по принципу (*) – см. выше.

Пример 2. Пусть П – задача проверки гамильтоновости бинарного отношения R на множестве M, |M| = n. (см. пример 1). Для любой задачи p∈П массив входных данных I – матрица бинарного отношения R на множестве M, |I| = |p| = n².

Рассмотрим этапы работы H – алгоритма над задачей p.

1. Недетерминированно генерируется слово c(I) = i₁i₂…i_n – перестановка элементов множества M.

2. Детерминированно проверяются для I и c(I) условия (1).

3. Выдается окончательный ответ «да» только если хотя бы для одного слова c(I) условия (1) выполняются.

Замечание 1. Изложенное выше понятие H- алгоритма является интуитивным, но может быть формализовано, например, с помощью модели недетермированной машины Тьюринга (см. [4], [5] и [6]).

Рассмотрим время работы H – алгоритма T(n):

На 1 этапе: t₁(I) = |c(I)| время на генерирование «подсказки» c(I).

На 2 этапе: t₂(I) – время проверки на пути вычисления, определенном подсказкой с(I).

T(n) = max_|I|=n(t₁(I)+t₂(I))

Таким образом H – алгоритм является полиномиальным, если T(n)=O(p(n)), то есть и длина подсказки t₁(I) = |c(I)| и время проверки t₂(I) ограничены некоторым полиномом p(n) от n = |I|.

Определение 5. Классом сложности NP называется класс всех тех алгоритмических задач, которые допускают решение хотя бы одним полиномиальным H – алгоритмом.

Таким образом класс NP представляет собой класс всех переборных задач разрешения, решаемых за полиномиальное время.

Очевидно, что любой детермированный алгоритм можно считать H – алгоритмом с единственной подсказкой c(I) (т. е. единственным путем вычисления). Если при этом детермированный алгоритм полиноминален, то t₁(I) = |c(I)| - длина пути вычисления и t₂(I) – время проверки ограничены полиномом p(n) и детерминированный полиномиальный алгоритм можно считать полиномиальным H – алгоритмом.

Отсюда следует включение классов .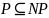

Есть много причин считать это включение строгим, но этот факт пока не доказан и представляет собой известную проблему теории алгоритмов

Определение 6. Задача распознавания называется NP - полной, если она принадлежит классу NP и любая задача из NP сводится к ней полиноминально.

К настоящему времени количество известных NP – полных задач выражается четырехзначным числом и постоянно появляются новые. Ни для одной из NP - полных задач не удалось на данный момент построить полиномиальный алгоритм, т. е. доказать её принадлежность классу P (это доказало бы гипотезу P = NP)