
§9. Эвристические алгоритмы решения переборных задач. «Жадные» алгоритмы.
Пусть решаемая задача относится к классу NP, то есть все её известные решения сводятся к перебору всех возможных вариантов для выбора оптимального.
Для решения можно воспользоваться одним из трёх подходов:
Если размер задачи небольшой, можно перебрать всевозможные варианты решения и выбрать оптимальный.
Использовать дополнительную информацию об исходной задаче, то есть её особые свойства, позволяющие исключить необходимость перебора всех вариантов.
Изменить постановку задачи искать не оптимальное решение, а близкое к оптимальному.
Алгоритмы, которые быстро находят приемлемое, но не оптимальное решение, называются эвристическими, а поиск решения с помощью таких алгоритмов называется эвристическим поиском.
Во многих случаях «почти оптимальное решение» можно считать вполне удовлетворительным, так как хорошие эвристические алгоритмы обеспечивают «стоимость» такого решения, лишь на несколько процентов отличную от оптимальной.
«Жадным» алгоритмом называется эвристический алгоритм, который на каждой отдельной стадии решения задачи выбирает тот вариант, который является локально оптимальным в том или ином смысле.
Не каждый «жадный» алгоритм гарантирует оптимальный результат в целом, несмотря на «оптимальность» каждого отдельного шага.
Рассмотрим важные для практики модельные задачи, к которым можно свести решение большого класса задач.
Пример 1. Задача коммивояжера – задача поиска в неориентированном полном графе с весовыми значениями рёбер такого простого цикла, включающего все вершины, у которого сумма «стоимостей» составляющих его рёбер будет минимальной.
Даны несколько городов (точек, вершин графа). Города соединены дорогами (рёбра графа), указаны протяжённости дорог (стоимость рёбер),каждые два города соединены дорогами (граф полный). Требуется найти такой маршрут – путь, исходящий из любого города, проходящий через каждый город ровно один раз и возвращающийся в исходную точку, протяжённость которого минимальна.
К задаче коммивояжера сводятся многие практические задачи (нахождение маршрутов минимальной стоимости, обход доски шахматным конём и др.)
Пусть задан неориентированный граф, вершинами которого являются точки на координатной плоскости, в качестве веса ребер принимается геометрическое расстояние между точками.

Рассмотрим «жадный» алгоритм (вариант алгоритма Краскала), который заключается в следующем: при просмотре ребер в порядке возрастания их веса очередное ребро принимается (включается в маршрут), если в сочетании с уже принятыми ребрами, оно:
Не приводит к появлению вершины со степенью 3 и более (повторному заходу в уже пройденный город).
Не образует цикл - замкнутый путь, в котором начало и конец совпадают (за исключением случая, когда это последний этап построения маршрута).
Найдем длину каждого ребра и расположим ребра в таблице в порядке возрастания их весов.
Ребро |
Вес |
|
de |
3 |
принимается |
bc |
5 |
принимается |
ab |
5 |
принимается |
ef |
5 |
принимается |
ac |
|
нет, цикл с (a,b) и (b,c) |
df |
|
нет, цикл с (d,e) и (e,f) |
be |
|
нет, повторный заход в b и e |
bd |
|
нет, повторный заход в b и d |
cd |
14 |
принимается |
bf |
|
нет, повторный заход в b |
ce |
|
нет, повторный заход в с и е |
ae |
|
нет, повторный заход в е |
ad |
|
нет, повторный заход в d |
af |
18 |
принимается. Окончание построения |
cf |
|
|
Алгоритм является «жадным», т.к. на каждом отдельном шаге выбирается локально оптимальный вариант – кратчайшее ребро удовлетворяющее условию 1 и 2, Но в целом полученный маршрут abcdef не является оптимальным, хотя лишь на 4% длиннее оптимального маршрута acdefb.
Пример 2. Задача раскраски графа. Каждой вершине графа нужно так задать цвет, чтобы никакие две соединенные ребром вершины не имели одинаковый цвет. При этом необходимо использовать минимальное количество цветов.
Задача принадлежит к классу NP, более того – является NP-полной.
«Жадный» алгоритм раскраски графа:
Выбрать произвольную незакрашенную вершину и назначить ей новый цвет.
Просмотреть список незакрашенных вершин. Для тех, которые не соединены с вершиной, закрашенной в новый цвет, также применить этот цвет.
Выбрать новый цвет и вернуться к шагу 1.
П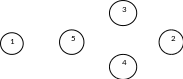 усть
дан граф и вершины его пронумерованы.
Реализуем для него указанный алгоритм.
усть
дан граф и вершины его пронумерованы.
Реализуем для него указанный алгоритм.
Первая незакрашенная вершина в порядке нумерации - 1 - закрашивается, например, красным.
В порядке нумерации 2 - красная, 3,4 и 5 – нет, т.к. соединены с 1 и 2.
Новый цвет – синий. Первая незакрашенная вершина 3 – синяя. Далее 4 синяя, 5 – нет, т.к. соединена с 3 и 4.
Новый цвет – зеленый. Последняя вершина 5 – зеленая.
Итого – 3 цвета.
Алгоритм «жадный», т.к. каждый новый цвет применяется к максимально большому числу вершин без возможности пропуска некоторых их них.
Если бы можно было после закраски 1 – красная, 2 пропустить и закрасить 3 и 4 красным, а затем 2 и 5 – синим, потребовалось бы 2 цвета. Поэтому полученное решение не оптимально.

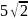
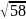
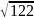
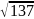
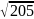
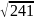
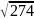
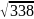 =13
=13